Лекция 3

2.2. Уравнения поля в дифференциальной форме.

Использование уравнений электромагнитного поля в интегральной форме для анализа электромагнитных процессов возможно лишь для весьма ограниченного числа случаев, когда имеет место симметрия объектов. Для практического решения задач более удобной является дифференциальная форма уравнений поля.

В уравнении (2.8) возьмем на поверхности s некоторую фиксированную точку с направлением нормали и осуществим предельный переход s  0, сохраняя малую окрестность вокруг рассматриваемой точки, разделив обе части уравнения на величину поверхности:

. (3.1)

Видно, что правая часть полученного равенства представляет проекцию вектора плотности полного тока на направление . Левая часть поэтому также может интерпретироваться как проекция некоторого вектора на это же направление. Этот вектор называется ротором или вихрем поля , а выражение для его проекции, следующее из (3.1) может быть взято за определение:

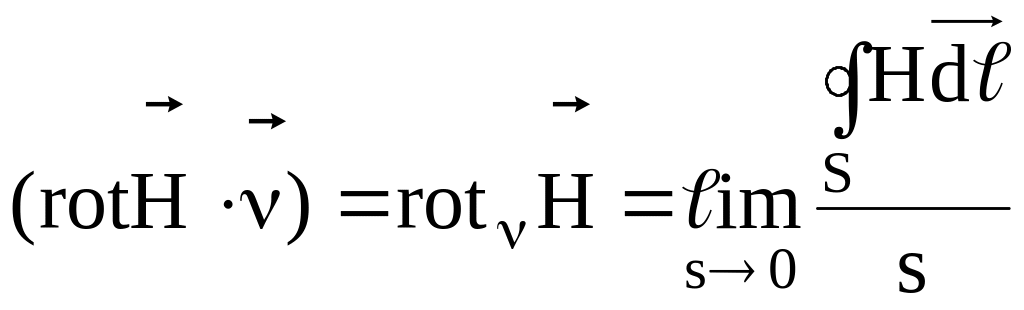. (3.2)

Сам rot может быть однозначно определен по трем проекциям на координате оси какой-либо системы координат. Выбирая в качестве последовательно орты декартовой системы координат и в качестве поверхностей s соответствующие прямоугольники уz, хz, ух легко вычислить проекции ротора на декартовы оси координат. В частности, проекция на ось х равна:

. (3.3)

Тогда сам rot может быть представлен в виде:

. (3.4)

Эта формула сворачивается в символической форме в векторное произведение символического вектора

и вектора

(3.5)

С помощью (3.1) от уравнения (2.8) можно перейти к закону полного тока в дифференциальной форме:

. (3.6)

Уравнение (2.9) можно записать в векторной форме по аналогии:

. (3.7)

Дифференциальная форма закона Гаусса также может быть получена из (2.10) с помощью соответствующего предельного перехода. Устремим к нулю объем V, сохраняя внутреннюю точку наблюдения, разделив на V обе части (2.9):

.

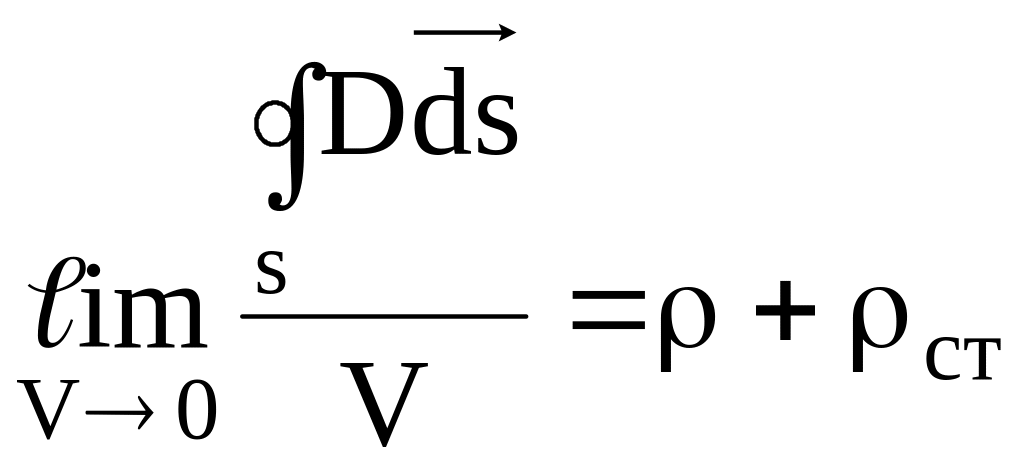Предел в левой части называется дивергенцией вектора :

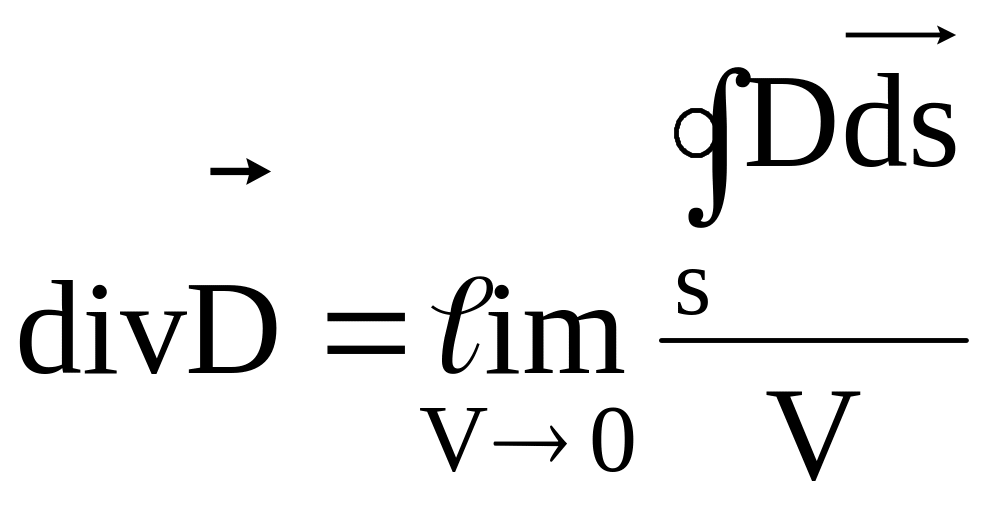. (3.8)

Взяв в качестве объема V прямоугольный параллелепипед хуz, ориентированный вдоль осей декартовой системы координат получим выражение для дивергенции через проекции вектора :

. (3.9)

Таким образом, уравнения (2.10) (2.11) приобретают соответственно вид:

, (3.10)

. (3.11)

Градиент потенциала может с помощью символического векторного оператора  записан как произведение вектора на скаляр:

grad  = .

Дифференциальные операторы rot, div, grad могут применяться повторно для получения дифференциальных уравнений более высокого порядка. Непосредственным вычислением можно установить, например:

rot grad   0, (3.12)

div rot  0, (3.13)

div grad  = . (3.14)

где ² =  - т.н. оператор Лапласа.

rot rot = grad div - ² . (3.17)

Последняя из приведенных формул справедлива только в декартовой системе координат, а оператор Лапласа в ней действует на декартовы составляющие вектора . Взяв оператор дивергенции от обеих частей (3.6) и учитывая (3.13) и (3.10) устанавливаем важное соотношение, закон сохранения заряда:

. (2.28)

Контрольные вопросы

1. Как определяется проекция ротора векторного поля на фиксированное направления?

2. Как выражается ротор векторного поля через свои проекции в декартовых координатах?

3. Дайте определение дивергенции векторного поля?

4. Как записываются операторы ротора, дивергенции и градиента через символический оператор ?

5. Как записывается закон полного тока в дифференциальной форме?

6. Как записывается обобщенный закон Фарадея в дифференцмальной форме?

7. Как записывается обобщенный закон Гаусса в дифференциальной форме?

8. Как записывается закон непрерывности магнитной индукции в дифференциальной форме?

9. Как записывается закон сохранения заряда в дифференциальной форме?