Контрольные вопросы

1. Какому уравнению удовлетворяют напряжение и ток в двухпроводной линии связи без потерь?

2. Какой физический смысл имеет каждое слагаемое в общем решении этого уравнения?

3. Как связаны между собой напряжение и ток в каждой из волн?

4. Какую схему замещения имеет сопротивление нагрузки длинной линии?

5. Как записать изображения падающего и отраженного напряжений в линии передачи с помощью теоремы запаздывания?

6. Нарисуйте эквивалентную схему для определения первоначальной падающей волны ?

7. Почему нельзя согласовать линию с произвольной нагрузкой?

8. Может ли коэффициент отражения быть отрицательным?

9. Чем завершается переходный процесс при подключении к линии с нагрузкой источника постоянного напряжения?

Лекция 9

3.4. Расчет поля помехи по известному распределению источников

Если установлены источники поля помехи и известно распределение тока в этих источниках, можно осуществить приближенную оценку электромагнитной обстановки ЭМО, создаваемой такими источниками. Предположим, что помехи распространяются в неограниченном однородном пространстве, т. е. пренебрегаем влиянием окружающих предметов. В дальнейшем электромагнитная обстановка может уточняться путем решения соответствующей граничной задачи. При этом поле, рассчитанное для однородного пространства, используется как известное первичное поле. Т.е. проводимый для однородного пространства расчет имеет как самостоятельное значение в качестве приближенной оценки ЭМО, так и служит необходимым промежуточным этапом, для точного решения. Пусть в однородном пространстве с параметрами ,  имеется заданное распределение токов , которое служит источником поля помехи . Проводимость пространства будем полагать равной нулю. Для получения расчетных соотношений для поля используют вспомогательные функции, через которые затем и вычисляют поле. Остановимся на одном из таких вариантов. Обратимся к уравнению соленоадальности магнитного поля:

. (9.1)

Поскольку оно выполняется тождественно для любого поля, можно полагать, что имеет представление

, (9.2)

где - некоторая векторная функция, определяемая с точностью до градиента скалярного потенциала  (rotgrad   0). Закон Фарадея с учетом введенной функции можно записать:

. (9.3)

Поскольку равенство нулю ротора является условием потенциальности поля, то имеет место его представление в виде градиента некоторого скалярного поля:

. (9.4)

Подставим выражение для поля из (9.2) и (9.4) в уравнение полного тока:

. (9.5)

Заменяя в декартовой системе координат двойной ротор согласно тождеству:

,

где ² – скалярный оператор Лапласа, применяемый к декартовым составляющим , получаем уравнение:

. (9.6)

Используя неоднозначность представления (9.2) потребуем выполнения так называемого условия калибровки:

. (9.7)

Пусть, например, первоначально введенные функции , не удовлетворяют этому условию. Тогда определив потенциал  из уравнения

.

Получим новые функции и :

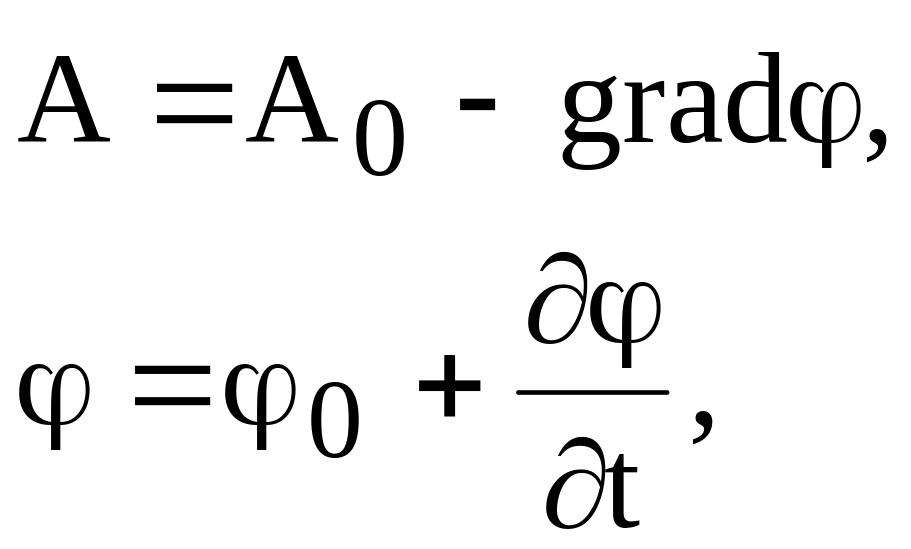
удовлетворяющее уравнению (9.7).

Запишем закон Гаусса с учетом представления поля из (9.4):

. (9.8)

Используя условие калибровки, получаем из (9.8)

. (9.9)

Объединяя с (9.6) получаем систему уравнений:

(9.10)

. (9.11)

где _ст. находится из j_ст. с помощью закона сохранения заряда

. (9.12)

Вектор и функция  называются векторным и скалярным электродинамическими потенциалами поля. При этом (9.10) эквивалентно трем скалярным уравнениям относительно декартовых компонент и . Поэтому достаточно рассмотреть методику решения одного скалярного уравнения (9.11).

Пусть в начале координат имеется точечный заряд Q, так что

, (9.13)

где - трехмерная дельта-функция Дирака. Для нахождения решения воспользуемся симметрией поля:  не может зависеть от угловых координат и является функцией координаты . Поэтому:

,

.

Складывая вторые производные по трем координатам получаем выражение для лапласиона поля, зависящего лишь от радиальной координаты

. (9.14)

Теперь левую часть (9.11) можно представить в форме:

.

Уравнение рассматриваемого вида уже встречалось при анализе длинных линий связи. Его решением является сумма двух произвольных дважды дифференцируемых функций:

,

а поскольку источник поля расположен в начале координат и отражение в однородном пространстве от какой-либо внешней границы отсутствует, функцию F₁ следует положить равной нулю и решение имеет вид сферической волны, распространяющейся от источника:

. (9.15)

Далее можно рассуждать следующим образом: поскольку в рассматриваемом случае источники симметричны (_ст. = _ст.(r)), можно проинтегрировать (9.11) по шагу переменного радиуса r с началом в точке расположения источника и применить теорему Остроградского-Гаусса:

. (9.16)

Здесь второе слагаемое в правой части имеет смысл дополнительных распределенных источников, попавших в шар V_с. Поле на поверхности шара дается выражением (9.15) и

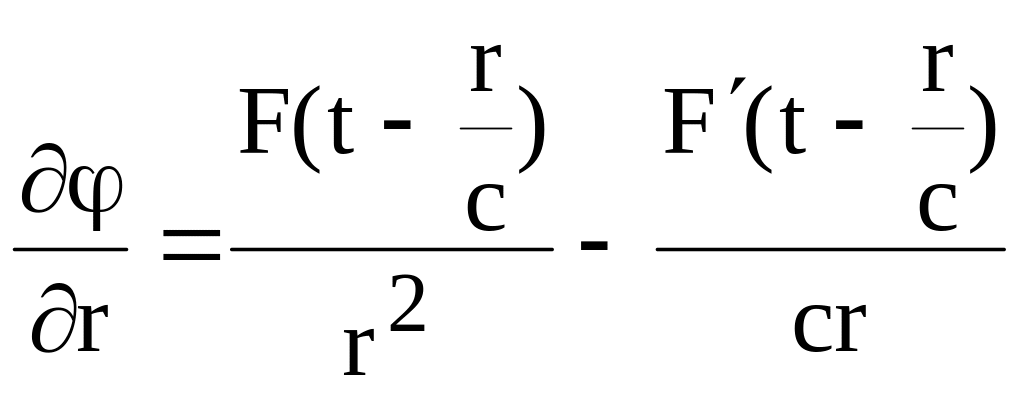. (9.17)

Подставим в (9.16) и перейдем к пределу полученного равенства r  0. Вклад объемного интеграла стремиться к нулю, как и второго слагаемого в правой части (9.17). Имеем:

, (9.18)

т.е.

. (9.19)

Окончательно получаем решение в виде так называемого запаздывающего потенциала:

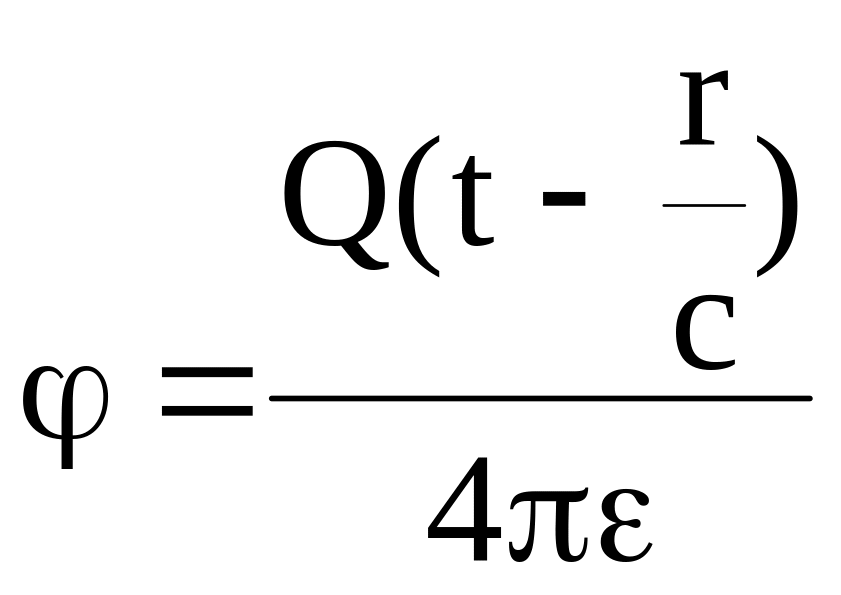. (9.20)

Если имеется произвольное распределение заряда, то можно рассматривать заряд в элементарном объеме dv как точечный с величиной _ст.dv и используя (9.20) получить потенциал в некоторой точке наблюдения в виде:

, (9.21)

где , - радиус-вектор элемента объема dv в точке интегрирования.

Понятно, что из совпадения уравнений (9.11) с уравнением для любой декартовой составляющей векторного потенциала можем записать для векторного потенциала решение в виде:

. (9.22)

Векторы электромагнитного поля определяются из (9.2) и (9.4)

, (9.23)

. (9.24)

Поскольку заданными считаются обычно сторонние точки необходимая для расчета плотность сторонних зарядов может быть найдена из закона сохранения заряда:

. (9.25)