Лекция 18

4.6. Экранирование локального источника многослойным экраном

Расчет многослойного экрана в предположении, что поле помехи является плоской волной, оказывается достаточно простым и вместе с тем слишком идеализированным, потому что не позволяет учесть ни размеров экрана, ни характеристик направленности реальных источников. Поэтому анализ распространения через экран поля локального источника является следующим шагом, позволяющим учитывать особенности экранирования реальных источников. Для простоты ограничимся рассмотрением точечного источника типа диполя малых по сравнению с длиной волны размеров. Из таких элементарных источников можно составить любой реальный источник. Источник типа диполя можно представить в виде линейного элемента тока малой длины:

, (18.1)

где - единичный вектор, задающий ориентацию источника.

Векторный потенциал этого тока записывается в виде:

где  - длина источника (<<), G = [exp(-i₀R)]/(4R) – функция Грина однородного пространства, зависящая от расстояния между точкой наблюдения и точкой размещения источника . Векторы поля получаются дифференцированием векторного потенциала:

(18.2)

Функцию Грина G(R) можно представить в виде известного разложения в двойной интеграл Фурье по пространственным частотам _х, _у:

, (18.3)

где ,

,

(18.4)

Двойные знаки в выражении для вектора частот (18.4) соответствуют неравенствам z z_d.

Т.е. функция Грина представлена в виде двойного интеграла плоских волн, распространяющихся в направлениях:

. (18.5)

Выразим векторы поля в соответствии с (18.2) с помощью (18.3) через интеграл плоских волн. Операция градиента сводится к умножения подынтегрального выражения в (18.3) на вектор . Внося постоянный вектор под знак интеграла и учитывая что , получаем

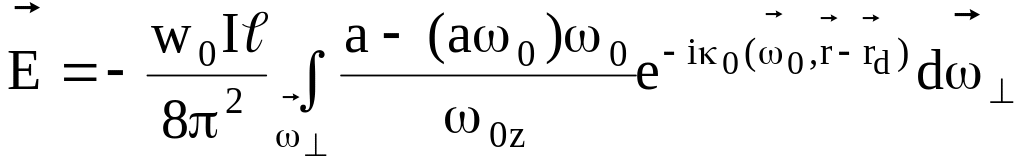, (18.6)

. (18.7)

Вектор удобно представить в виде:

, (18.8)

где единичный вектор определяет положение плоскости падения:

,

где s₀, c₀ в соответствии с введенными в предыдущем разделе обозначениями равны синусу и косинусу угла падения. Синус угла падения при этом в (18.6), (17.7) может принимать значения больше 1, а косинус соответственно комплексные. Разложим комплексный вектор в подынтегральном выражении (18.6) на составляющие, поляризованные в плоскости падения и перпендикулярные плоскости падения. Представим в виде составляющих по ортам, связанных с плоскостью падения:

, (18.9)

где - единичный вектор, перпендикулярный плоскости падения.

.

Откуда:

Учитывая, что имеем:

. (18.10)

Полученное соотношение можно истолковывать как разложение поля каждой плоской волны на составляющие, поляризованные в плоскости падения и перпендикулярно плоскости падения:

, (18.11)

где ,

, (18.12)

,

.

- единичные векторы, определяющие направление соответствующих поляризаций.

Для того, чтобы применить соотношения для многослойного экрана , приведенные в предыдущем разделе, необходимо привести в соответствие обозначения. Пусть диполь размещен в области перед экраном (i =0) в точке . Тогда

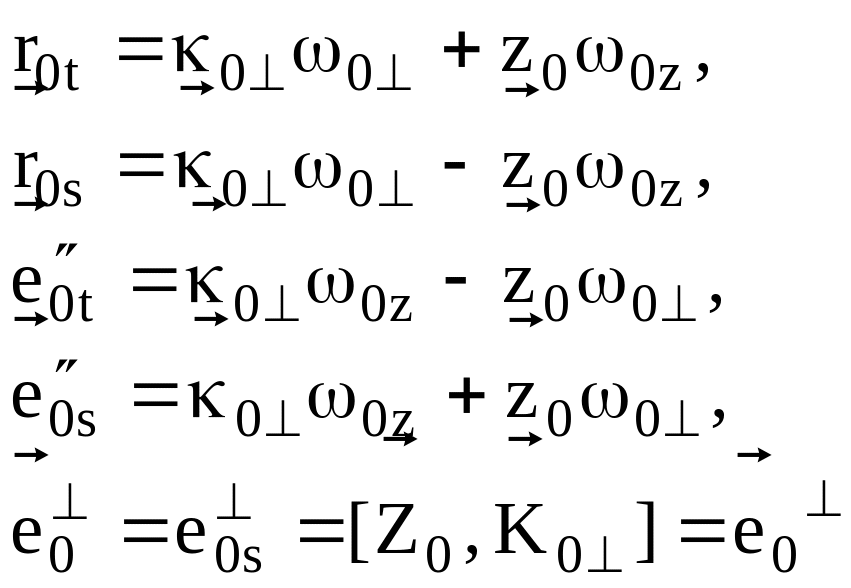(18.13)

Точка наблюдения вблизи экрана удовлетворяет условию z > z_d (z_d = -d₀). Поэтому для падающего поля имеем

, (18.14)

где ,

.

Отраженное поле ищем в аналогичном (18.14) представлении:

. (18.15)

Поле в произвольной i-ой области запишется теперь в следующем виде:

, (18.16) , (18.17)

где единичные векторы направлений падающей и отраженной волн соответственно равны:

,

,

а единичные векторы, определяющие направления полей падающей и отраженной волн, поляризованных в плоскости падения, определяются соотношениями:

,

.

В соответствии с обобщенным законом преломления:

, (18.18)

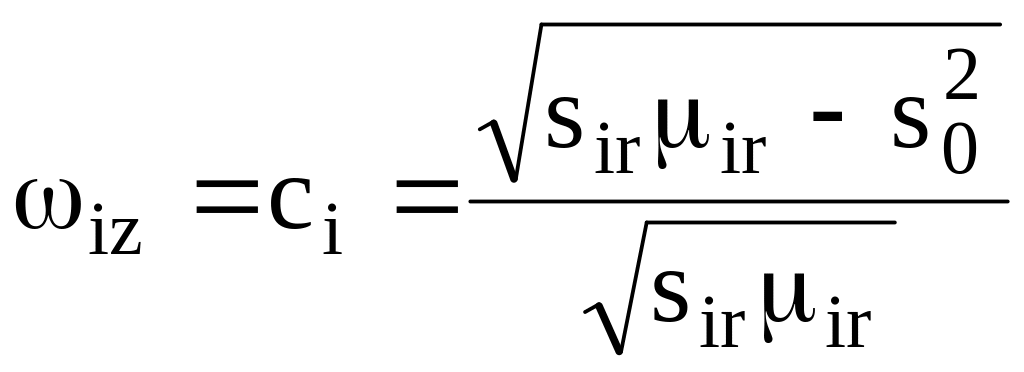, (18.19)

т.е. синус и косинус угла падения в i-ой области выражаются через единственный параметр s₀ – синус внешнего угла падения.

В соответствии с (18.16), (18.17) и формулами предыдущего раздела получаем поле i-ой области:

. (18.20)

Для удобства обозначений радиус вектор представим в виде:

.

Применяя теперь формулы предыдущего раздела, получим:

, (18.21)

, (18.22)

,

.

При этом при i = 1 имеем частное значение Т_0,1 = Т₀. Приведенные формулы не могут быть непосредственно применены при d₀ = 0, z = 0, поскольку интегралы расходятся. В этом случае поле может быть получено введением малого, но конечного значения d₀, или выделением особенности в подынтегральном выражении. Т.о. мы познакомились с методикой расчета многослойного экрана при защите от локального источника помех.