Контрольные вопросы

1. Какие граничные для касательных составляющих магнитного поля выполняются на границе магниного экрана и воздуха?

2. Какие граничные условия выполняются на границе магнитного экрана и воздуха для нормальной составляющей магнитной индукции?

3. Можно ли создать аналог электростатического проводящего экрана для экранирования постоянного магнитного поля?

4. На чем основана работа магнитного экрана?

5. Чем, кроме эксперимента можно подтвердить справедливость предположения об однородности магнитного поля внутри шарового тела при внесении его во внешнее однородное магнитное поле?

6. Точно или приближенно выполняется предположение о том, что внешнее поле, индуцируемое магнитным шаром во внешнем однородном поле, имеет характер поля магнитного диполя?

7. Как зависит магнитное поле диполя от угловой координаты, отсчитываемой от оси, параллельной моменту диполя?

8. Какова эффективность экранирования магнитного поля шаровой оболочкой из магнитного материала?

9. Можно ли использовать аналог магнитного экрана для экранирования электрического поля?

Лекция 15

4.3. Основы теории электромагнитного экранирования

Переменные электромагнитные поля помех в зависимости от скорости из изменения требуют применения весьма разнообразных методов экранирования. Медленно меняющиеся, так называемые квазистатические поля могут с некоторыми изменениями экранироваться методами электростатического и магнитостатического экранирования. Новым обстоятельством здесь является возможность использования проводящих экранов для экранирования электромагнитного поля. В проводящей оболочке, внесенной в переменное магнитное поле, возникают за счет электромагнитной индукции переменные токи, магнитное поле которых направлено против экранируемого поля и результирующее поле оказывается ослабленным.

Условно критерием, когда необходимо применять электромагнитное экранирование, служит степень возбуждения токов смещения в экране. Для моделирования происходящих при этом процессов возможен единообразный подход. Рассмотрим спектральное представление полей в виде интегралов Фурье и запишем уравнения Максвелла в комплексной форме. В объеме экрана V_э уравнения запишем в виде:

(15.1)

В окружающий экран области V_е (для замкнутого экрана она состоит из двух частей: области внутри экрана и области вне экрана) удовлетворяются следующие уравнения:

(15.2)

Для проcтоты будем полагать, что область V_е однородна, а параметры _е, _е вещественны и постоянны. Считаем также, что источники поля помехи известны и ограничены некоторой областью V_s  V_е. Поле, создаваемое этими источниками в отсутствии экрана, обозначим через . При этом, поскольку в отсутствие экрана область V_е однородна и безгранична, поле может быть рассчитано по известным формулам раздела 9 с учетом синусоидального поля и комплексной формы его представления. Операции дифференцирования по времени соответствует умножение на i и скалярный потенциал из уравнения калибровки однозначно выражается через векторный потенциал:

. (15.3)

Так что поля можно выразить через векторный потенциал:

, (15.4)

, (15.5)

где векторный потенциал выражается в виде:

, (15.6)

где G – так называемая функция Грина однородного пространства:

, (15.7)

(R= - расстояние от точки наблюдения до точки интегрирования ). Множитель _е в формуле для векторного потенциала (15.6) для удобства опущен. Полное поле в области V_е вне экрана можно представить в виде суммы поля и поля рассеяния, возникающего из-за влияния экрана. Для исследования структуры этого поля преобразуем уравнения (15.1) следующим образом:

(15.8)

, (15.9)

где токи и в правой части сами выражаются через вектора поля:

, (15.10)

. (15.11)

Эти токи, учитывающие влияние экрана, называются токами поляризации. Теперь формально поле во всем пространстве описывается одинаковыми уравнения. Дополнительное поле, возникающее из-за наличия экрана, можно выразить через токи (15.10) (15.11). Можно воспользоваться формулами (15.4) (15.5) и временно положить =0. Затем, обратив внимание на то обстоятельство, что при =0 и 0 уравнения симметричны с точностью до знака правой части и обозначений снова использовать те же формулы. Поэтому можно ограничиться частным случаем немагнитных экранов и принять =0 (  _е).

Поле в объеме экрана V_э складывается из поля Е₀ и поля, созданного токами .

. (15.12)

Внося постоянный множитель 1/(i_е) под знак интеграла получим следующее уравнение относительно электрического поля внутри экрана:

, (15.13)

где - относительная диэлектрическая проницаемость экрана.

Уравнения, в которых неизвестная функция входит под знак интеграла, называются интегральными. В данном случае мы имеем так называемое интегральное уравнение Фредгольма II-го рода, у которого неизвестная функция не только входит под знак интеграла, но и в виде внеинтегрального слагаемого. Для этих уравнений разработана достаточно полная теория и численные методы решения. С этими методами мы познакомимся подробнее в разделе, посвященном оценке электромагнитной обстановки.

После решения уравнения (15.13) и нахождения поля в объеме экрана V_э находим поле рассеяния с помощью соотношения:

. (15.14)

Отметим особенности применения интегрального уравнения (15.13) к экранам. В уравнении (15.13) использовано частотное представление электромагнитного поля и оно справедливо для случая  = 0, т.е. для электростатического экранирования. Комплексная диэлектрическая проницаемость позволяет учитывать одновременно вклад токов смещения и токов индукции (вихревых токов). Учет магнитных свойств осуществляется добавлением в уравнение (15.13) дополнительного слагаемого , обусловленного магнитными токами поляризации:

, (15.15)

где может быть выражено через электрическое поле с помощью уравнения индукции:

. (15.16)

Электрическое поле, создаваемое магнитными токами поляризации можно представить через векторный магнитный потенциал:

, (15.17)

где выражается через магнитные токи поляризации с помощью выражения аналогичного (15.6):

. (15.18)

в развернутом виде можно теперь записать таким образом:

. (15.19)

Добавление (15.19) в уравнение (15.13) делает это уравнение интегро-дифференциальным, т.к. искомая функция входит под знак дифференциального оператора rot. Разумеется это усложняет алгоритм решения. Однако можно использовать следующие векторные преобразования:

, (15.20)

где .

Подставляя (15.20) в (15.19) и используя формулу:

,

получаем:

. (15.21)

Т.о. уравнение (15.13) для магнитодиэлектрических экранов можно записать в виде:

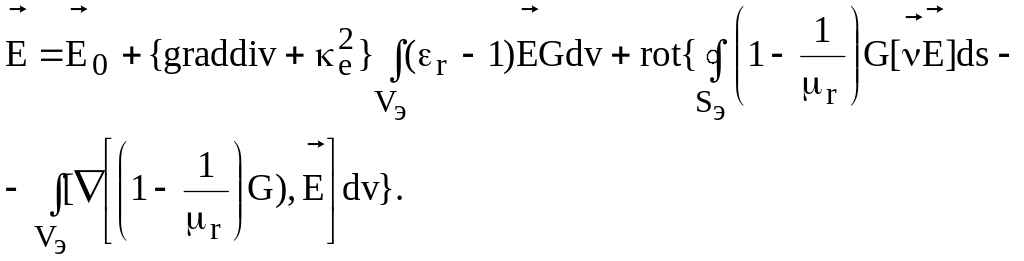(15.22)

Т.е. с учетом магнитных свойств можно получить интегральное уравнение относительно электрического поля. Однако теперь в отличие от (15.13) кроме объемных интегралов уравнение содержит интеграл по поверхности. Такое интегральное уравнение называется нагруженным.

Говоря о численных методах решения, мы ограничимся для простоты уравнением (15.13). Обычно уравнение сводят к системе линейных алгебраических уравнений (СЛАУ). В простейшем случае это можно сделать следующим образом. Область V_э разбивают на элементарные ячейки V_i, настолько малые, что в пределах каждой ячейки изменениями поля можно пренебречь и считать, что это значение поля соответствует середине ячейки. Объемный интеграл представляется в виде суммы интегралов по отдельным ячейкам, где значение поля выносится за знак интеграла по ячейке V_i. Помещая последовательно точку наблюдения в середину каждой ячейки. получаем СЛАУ с размерностью, соответствующей числу ячеек.

Метод интегральных уравнений обладает несомненным преимуществом общности и может быть использован для экранов произвольной формы и даже для неоднородных экранов. Но вместе с тем, как и любой численный метод не позволяет выявлять какие-либо закономерности при однократном решении какой либо задачи. Для их выявления необходим большой объем численных экспериментов. В этом смысле любое аналитическое решение в виде замкнутых формул имеет большую ценность.