Контрольные вопросы

1. Какие линии связи могут быть представлены в виде многопроводной направляющей системы?

2. Какие особенности имеют помехи в коротких многопроводных линиях связи?

3. С помощью каких параметров учитывается проникновение помех за счет связей по электрическому полю?

4. Чем отличаются емкостные коэффициенты от частичных ёмкостей?

5. Как определяется погонная ёмкость двухпроводной линии?

6. Как записываются потенциальные коэффициенты в многопроводной линии с проводниками круглого сечения?

7. При каких условиях поле двухпроводной линии можно считать двумерным?

8. Откуда следует симметрия матрицы потенциальных коэффициентов?

9. Симметрична ли матрица емкостных коэффициентов?

Лекция 11.

3.6. Перекрестные помехи за счет магнитных связей в многопроводных линиях

Токи в проводниках многопроводной линии порождают магнитные поля, соответственно, магнитные связи между отдельными линиями. Поскольку число линий в многопроводной шине может быть достаточно большим учет этих связей с помощью коэффициентов взаимоиндуктивности представляет собой достаточно громоздкую, и , главное, неблагодарную процедуру. Изменение схема включения проводников шины требует и перерасчеты этих коэффициентов. Здесь мы рассмотрим универсальный и достаточно простой подход к этой проблеме, основанный на связи напряженности электрического поля индукции с векторным потенциалом. При изменении магнитной индукции (и, соответственно, векторного потенциала) в проводниках появляется напряжённость электрического поля.

. (11.1)

Это электрическое поле отличается от потенциальных полей, рассмотренных в предыдущей теме и имеющих поперечную по отношению км осям проводников ориентацию, и создает в каждом проводнике системы э.д.с. индукции, равную

. (11.2)

П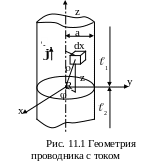 оскольку проводники параллельны и токи текут только вдоль оси z, векторный потенциал имеет только одну составляющую

A, (11.3)

так же как и токи . Рассмотрим векторный потенциал, создаваемый одиночным проводником, круглого сечения в котором течёт ток I. Будем предполагать, что общая длина проводника L много больше его радиуса. Рассчитаем вначале частное значение векторного потенциала на оси проводника на достаточном удаление от его концов (рис. 11.1)

Поместив начало координат в точку наблюдения, запишем выражение для векторного потенциала в виде

. (11.4)

Сигналы в современных электронных устройствах передаются с помощью быстроменяющихся токов. При этом имеет место сильный скин-эффект и весь ток в проводнике сосредоточен на его поверхности с поверхностной плотностью :

. (11.5)

Выражение для векторного потенциала приобретает вид:

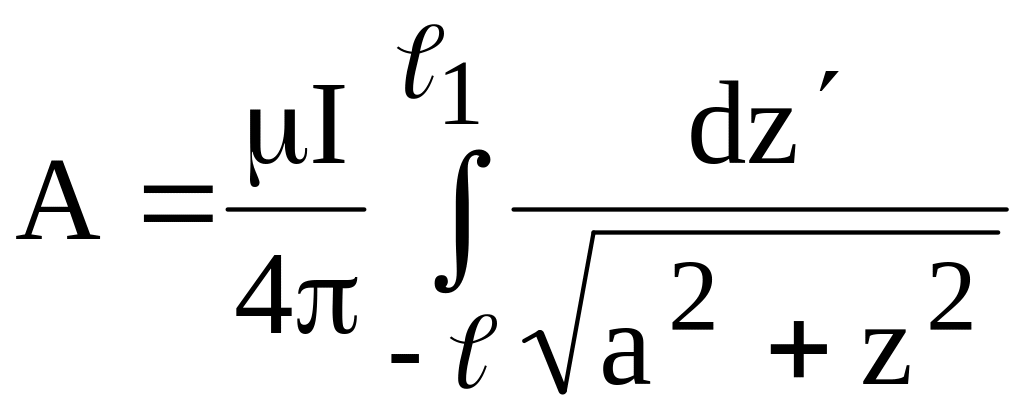. (11.6)

Вычисляя значение интеграла получаем следующее его значение:

. (11.7)

Тем самым вычислено частное значение векторного потенциала при =0.

С другой стороны внутри проводника плотность тока равна нулю и векторный потенциал удовлетворяет уравнению

. (11.8)

В виду симметрии А должно зависеть только от координаты . Левая часть представляет собой двумерный оператор divgrad A и интегрируя (11.8) по кругу переменного радиуса  < а и применяя двумерный аналог теоремы Остроградского-Гаусса получим:

. (11.9)

Откуда непосредственно интегрируя по  получаем

А = const = C. (11.10)

Этот результат должен согласоваться с (11.7) и поэтому во всей внутренней области векторный потенциал должен иметь значение:

а. (11.11)

Во всей области 0 уравнение для векторного потенциала можно записать с помощью -функции в правой части в выражении для плотности тока:

. (11.12)

Интегрируя (11.12) по кругу получаем равенство:

,

из которого следует:

(11.13)

Произвольную постоянную С₁ найдём из условия непрерывности векторного потенциала при =а. Т.Е. в этом случае значения (11.11) и (11.13) должны совпадать. Окончательное выражение для векторного потенциала одиночного проводника для быстропеременных токов приобретает вид:

A= (11.14)

Поле индукции в каждом проводнике многопроводной линии складывается из поля индукции самого проводника и полей наводимых соседними проводниками:

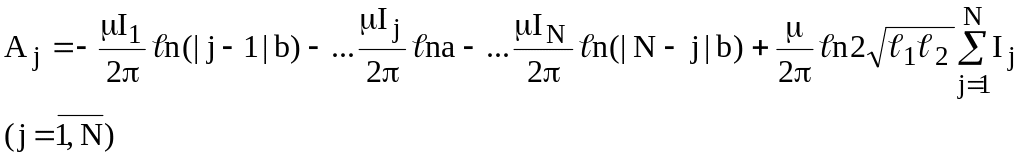(11.15)

Последнее слагаемое исчезает т.к. алгебраическая сумма токов в многопроводной линии в отсутствии заземления или обратной шины должна равняться нулю.

Таким образом учет магнитных связей в многопроводной линии сводится теперь к включению в схему замещения в каждый проводник многопроводной линии э.д.с. индукции

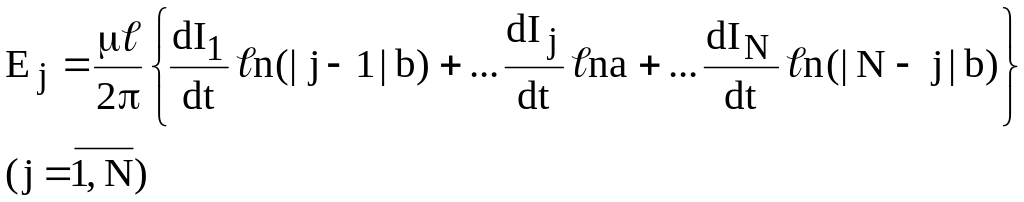(11.16)

В качестве элементарного примера рассмотрим двухпроводную линию с токами I₁ = I и I₂ = -I. В соответствии с (11.14) имеем:

С учетом обхода всей цепи содержащей данную линию общая э.д.с. индукции в линии составляет

,

а, соответственно, индуктивность всей линии составляет

. (11.17)

Значение индуктивности линии на единицу длины полностью согласуется с известными по литературе:

. (11.18)