
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •§4. Линейная зависимость векторов и ее свойства
- •Примеры
- •Свойства линейно зависимой системы векторов
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •§8. Векторное произведение двух векторов
- •Геометрические свойства векторного умножения векторов
- •Алгебраические свойства векторного умножения векторов
- •Применение векторного произведения
- •Задания для самостоятельной работы
- •§9. Смешанное произведение трех векторов
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения трех векторов
- •§10. Понятие аффинной и прямоугольной декартовой
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Прямая линия на плоскости Лекция 9 Прямая в аффинной системе координат
- •§15. Различные уравнения прямой
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •§18. Уравнение прямой, заданной точкой и
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •§20. Различные уравнения плоскости
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§22. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§23. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§24. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§25. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§26. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
§3. Умножение вектора на число
Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.
Произведением
вектора
на действительное число
называется вектор
![]() ,
обозначаемый через
,
обозначаемый через
![]() и удовлетворяющий двум условиям:
и удовлетворяющий двум условиям:
его длина
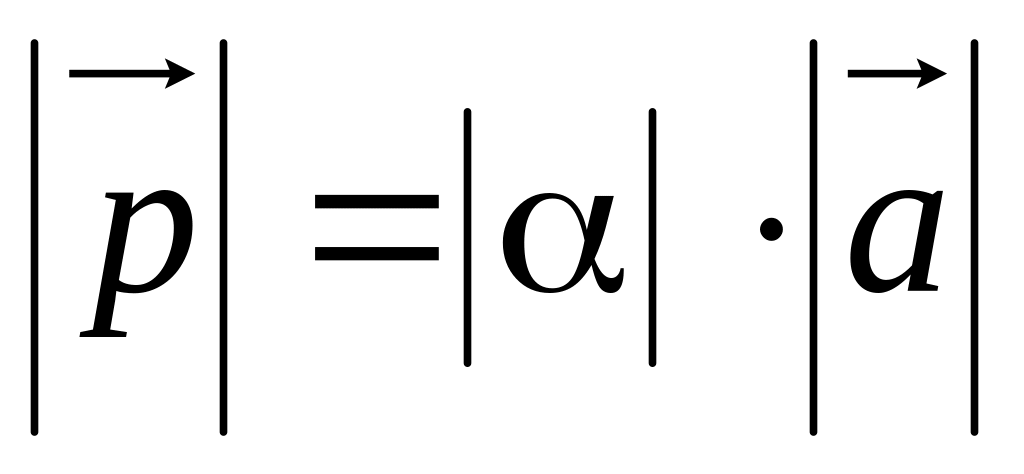 ;
;если
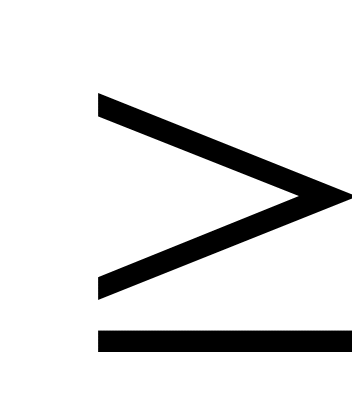 0,
то
0,
то
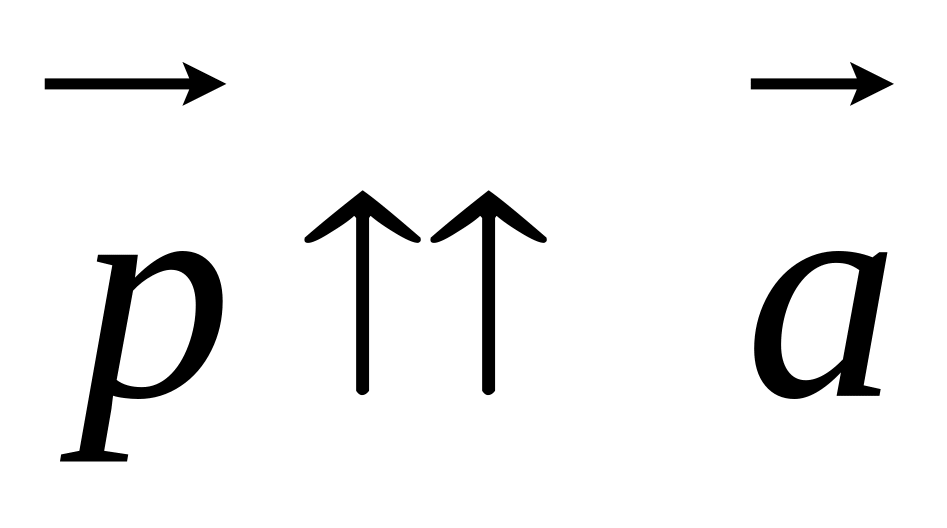 ;
если
;
если
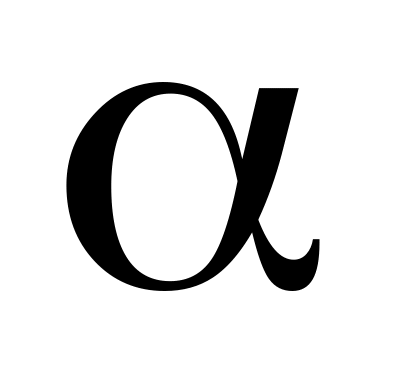 <0,
то
<0,
то
 .
.
Алгоритм построения произведения вектора число таков.
Берем произвольную
точку М.
Проводим луч
![]() ,
сонаправленный с вектором
,
если
0,
и противоположно направленный с вектором
,
если
<0.
На луче
от начала М откладываем отрезок MP,
длина которого в
,
сонаправленный с вектором
,
если
0,
и противоположно направленный с вектором
,
если
<0.
На луче
от начала М откладываем отрезок MP,
длина которого в
![]() раз больше длины вектора
.
Вектор
раз больше длины вектора
.
Вектор
![]() - искомый вектор
- искомый вектор
![]() .
.
Продемонстрируем
этот алгоритм на конкретном примере.
Построим вектор
![]() ,
если
- данный вектор.
,
если
- данный вектор.
Возьмем произвольную
точку А.
Так как
![]() <0,
то проводим луч
<0,
то проводим луч
![]() (рис. 7). На луче
строим такую точку С,
что
(рис. 7). На луче
строим такую точку С,
что
![]() .
Тогда
.
Тогда
![]() - искомый вектор.
- искомый вектор.

Свойства умножения вектора на число
10.
![]() и
и
![]()
![]() .
.
20.
![]()
![]() .
.
30.
![]()
![]()
![]() .
.
40.
![]() .
.
Теорема 1 (о
коллинеарных векторах).
Пусть
![]() .
Векторы
и
коллинеарны тогда и только тогда, когда
существует такое действительное число
,
что
.
Векторы
и
коллинеарны тогда и только тогда, когда
существует такое действительное число
,
что
![]() .
.
Т
еорема
2 (о компланарных векторах).
Пусть
![]() ||
||
![]() .
Векторы
.
Векторы
![]() компланарны тогда и только тогда, когда
существуют такие действительные числа
и ,
что
компланарны тогда и только тогда, когда
существуют такие действительные числа
и ,
что
![]() .
.
Задания для самостоятельной работы
1. Начертите
произвольный вектор
.
Постройте векторы
![]()
![]()
![]()
![]() .
.
2. Даны векторы
и
.
Постройте векторы
![]()
![]() .
.
3. Упростите
выражение
![]() .
.
4. Будут ли векторы
![]() и
и
![]() коллинеарны и почему, если
коллинеарны и почему, если
![]() ?
?
5. Будут ли векторы
![]()
![]() и
компланарны и почему?
и
компланарны и почему?
Лекция 2
Линейная зависимость векторов
§4. Линейная зависимость векторов и ее свойства
Линейной
комбинацией векторов
![]() называется
вектор
называется
вектор
![]() ,
где
,
где
![]()
![]() .
.
Примеры линейных комбинаций:
1. Вектор
![]() есть линейная комбинация векторов
есть линейная комбинация векторов
![]() (здесь
(здесь
![]() ).
).
2. Вектор
![]() есть линейная комбинация векторов
(здесь
есть линейная комбинация векторов
(здесь
![]() ).
).
Система векторов
называется
линейно
зависимой,
если существуют такие действительные
числа
![]() ,
не все равные 0 одновременно, что
выполняется векторное равенство:
,
не все равные 0 одновременно, что
выполняется векторное равенство:
![]() .
.
Если равенство
выполняется только при
![]() ,
то система векторов
называется
линейно
независимой.
,
то система векторов
называется
линейно
независимой.
Примеры
1. Система векторов
![]() линейно зависима, т.к. если возьмем
линейно зависима, т.к. если возьмем
![]() ,
то получим, что
,
то получим, что
![]() ,
т.е. существуют такие действительные
числа
,
т.е. существуют такие действительные
числа
![]() ,
не все равные 0 одновременно (
,
не все равные 0 одновременно (![]() ),
что выполняется равенство
),
что выполняется равенство
![]() .
.
2. Система двух
неколлинеарных векторов
и
линейно независима, т.к. сумма двух
неколлинеарных векторов
![]() и
и
![]() равна нулевому вектору
равна нулевому вектору
![]() только при
только при
![]() .
.
Свойства линейно зависимой системы векторов
10. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
□ Пусть система,
состоящая из одного вектора
,
линейно зависима. Докажем, что вектор
![]() .
.
Из определения
линейно зависимой системы следует, что
существует
![]() такое, что
такое, что
![]() .
Так как первый сомножитель в левой части
не равен 0, то второй сомножитель должен
быть нулевым вектором, т.е.
.
.
Так как первый сомножитель в левой части
не равен 0, то второй сомножитель должен
быть нулевым вектором, т.е.
.
Пусть, обратно,
.
Докажем, что система, состоящая из одного
вектора
,
линейно зависима. Левую часть равенства
можно записать в виде
![]() ,
следовательно,
,
следовательно,
![]() ,
т.е. существует
такое, что
.
По определению линейно зависимой системы
векторов система
линейно зависима. ■
,
т.е. существует
такое, что
.
По определению линейно зависимой системы
векторов система
линейно зависима. ■
20. При n>1 система векторов линейно зависима тогда и только тогда, когда хотя бы один из них является линейной комбинацией остальных векторов этой системы.
□ Пусть система векторов линейно зависима. Докажем, что один из ее векторов является линейной комбинацией остальных векторов этой системы.
По определению линейно зависимой системы векторов существуют числа , не все равные 0 одновременно, такие, что
.
Пусть для
определенности
![]() ,
где к
– одно из чисел 1,
2, ...,n.
Перенесем все слагаемые, кроме
,
где к
– одно из чисел 1,
2, ...,n.
Перенесем все слагаемые, кроме
![]() ,
из левой части равенства в правую и
разделим обе части равенства на
:
,
из левой части равенства в правую и
разделим обе части равенства на
:
![]() .
.
Следовательно,
вектор
![]() есть линейная комбинация векторов
есть линейная комбинация векторов
![]() .
.
Пусть теперь один
из векторов системы
,
например,
,
является линейной комбинацией векторов
.
Докажем, что
система векторов
![]() линейно
зависима.
линейно
зависима.
По условию
![]() .
Перенесем
в правую часть и поставим это слагаемое
между
.
Перенесем
в правую часть и поставим это слагаемое
между
![]() и
и
![]() :
:
![]() .
.
Таким образом,
существуют такие числа
![]() ,
не все равные 0 одновременно, что
выполняется векторное равенство
,
не все равные 0 одновременно, что
выполняется векторное равенство
![]() .
.
Следовательно, система векторов линейно зависима. ■
30. Если часть данной системы векторов линейно зависима, то и вся система линейно зависима.
□ Пусть дана
система векторов
и известно, что ее подсистема
![]() <n,
линейно зависима. Тогда существуют
такие числа
<n,
линейно зависима. Тогда существуют
такие числа
![]() ,
причем
,
причем
![]() ,
что
,
что
![]() .
.
Тогда
![]() ,
,
т.е. нашлись числа
![]() ,
причем
,
следовательно, система
линейно
зависима. ■
,
причем
,
следовательно, система
линейно
зависима. ■
40. Система линейно независимых векторов не содержит нулевого вектора.
□ Пусть система
линейно независима. Предположим, что
она содержит
![]() .
По свойству 10
система
линейно зависима. Тогда по свойству 30
вся система
линейно зависима. Получили противоречие
с условием. ■
.
По свойству 10
система
линейно зависима. Тогда по свойству 30
вся система
линейно зависима. Получили противоречие
с условием. ■
50. Если система векторов линейно независима, то любая ее часть линейно независима.
□ Предположим, что существует часть данной системы, являющаяся линейно зависимой. Тогда по свойству 30 вся данная система должна быть линейно зависимой. Получили противоречие с условием. ■
60.
Система векторов
![]() линейно зависима тогда и только тогда,
когда
||
.
линейно зависима тогда и только тогда,
когда
||
.
□ Пусть система
векторов
линейно зависима. Тогда по свойству 20
или
![]() ,
или
.
По теореме о коллинеарных векторах
||
.
,
или
.
По теореме о коллинеарных векторах
||
.
Пусть
||
.
Если один из векторов нулевой, например,
,
то по свойству 40
система
,
линейно зависима. Если
![]() ,
то по теореме о коллинеарных векторах
,
то по теореме о коллинеарных векторах
![]() .
Так как
.
Так как
![]() ,
то система векторов
линейно зависима. ■
,
то система векторов
линейно зависима. ■
Аналогично, пользуясь теоремой о компланарных векторах, можно доказать свойство
70. Система векторов линейно зависима тогда и только тогда, когда эти векторы компланарны.
