Основная метрическая задача

Теорема 3(расстояние между двумя точками в координатах). Если в прямоугольной декартовой системе координат , , то расстояние АВ между точками А и В находится по формуле:

.

Учитывая, что , и используя формулы для нахождения длины вектора в координатах, получаем:

.

Формулы, доказанные в теоремах 1 и 2, можно использовать и в аффинной, и в прямоугольной декартовой системе координат, а формулу из теоремы 3 – только в прямоугольной декартовой системе координат.

Задания для самостоятельной работы

1. Найдите координаты точки А, если В(3;0;-2), .

2. С – середина отрезка АВ. Найдите координаты точки В, если А(1;0;-4), С(3;1;0).

3. Точки Р и Q лежат внутри отрезка АВ, причем АР=РQ=QВ. Найдите (ВQ,А).

4. На плоскости дан отрезок [АВ]. Постройте точку С, делящую направленный отрезок в отношении ; .

5. Известны координаты вершин треугольника АВС: А(4;3), В(0;5),С(-2;2). Пользуясь теоремой, обратной теореме Пифагора, выясните, будет ли этот треугольник прямоугольным.

6. Можно ли вывести формулы для нахождения расстояния между двумя точками, координаты которых даны в аффинной системе координат?

Лекция 8 Формулы преобразования координат

§12. Преобразование аффинной системы координат

Возьмем на плоскости две аффинные системы координат и . Первую назовем старой, вторую - новой. Пусть М – произвольная точка плоскости, которая в старой системе имеет координаты х,у, а в новой системе - координаты (рис. 39).

З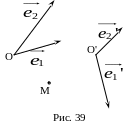 адача преобразования координат состоит в следующем: зная координаты нового начала и новых координатных векторов в старой системе:

, , , (3)

выразить координаты х,у точки М в старой системе координат, через координаты этой точки в новой системе.

Из формул (3) следует, что

; ; . (4)

(по правилу треугольника).

Так как , , то по определению координат точки , , т.е. ; .

Тогда, используя формулы (4), получим:

,

т.е. ,

откуда находим:

(5) ;

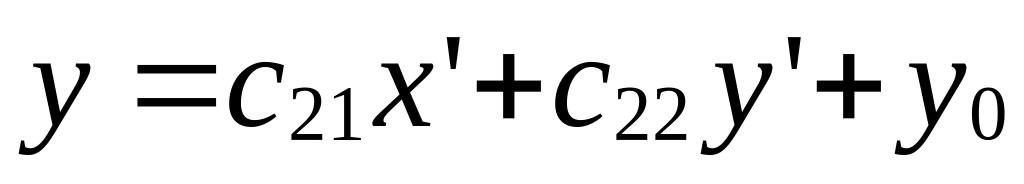
. Так выражаются координаты х,у произвольной точки М в старой системе через ее координаты в новой системе .

Формулы (5) называются формулами преобразования аффинной системы координат.

Коэффициенты , при - координаты нового вектора в старой системе ; коэффициенты , при - координаты нового вектора в старой системе, свободные члены , - координаты нового начала в старой системе:

Координаты точки М

в новой системе

Таблица называется матрицей перехода от базиса , к базису , .

Частные случаи преобразования аффинной системы координат

1. Перенос начала.

При этом преобразовании , , а (рис. 40).

Найдем координаты векторов и в старой системе, т.е. , , и :

  , ;

  , .

Тогда формулы (5) примут вид:

(6)

Формулы (6) называются формулами переноса начала.

2. Замена координатных векторов.

При этом преобразовании системы координат имеют общее начало и отличаются координатными векторами (рис. 41).

Так как , то , . Тогда формулы (5) примут вид:

; .

(7)

Формулы (7) называются формулами замены координатных векторов.