§20. Различные уравнения плоскости
в аффинной системе координат
Плоскость
в пространстве можно задать точкой и
двумя неколлинеарными векторами,
параллельными ей (или принадлежащими
ей) или тремя точками, не лежащими на
одной прямой. В первом случае этот факт
будем обозначать так:
;
во втором –
.
Пусть в пространстве
дана аффинная система координат
.
1. Уравнение плоскости, заданной точкой и двумя неколлинеарными векторами.
П
усть
,
||
(рис. 65),
в системе
.
тогда и только
тогда, когда векторы
и
компланарны,
т.е. их смешанное
произведение
.
Переходя к координатам, получим уравнение:
.
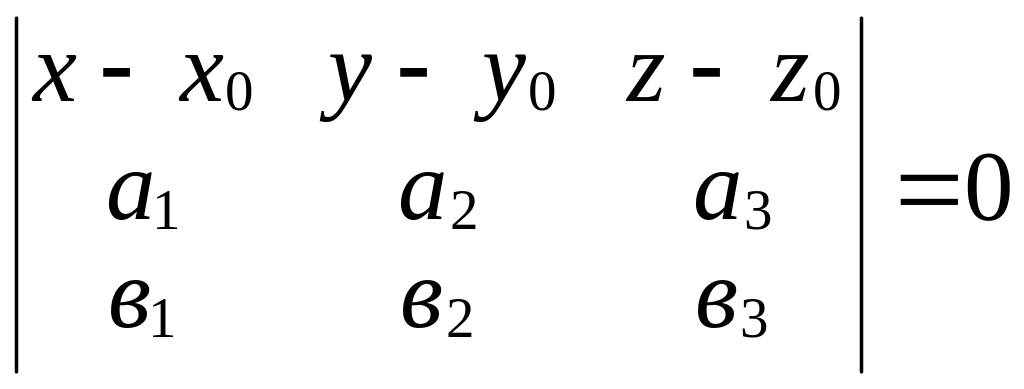(20)
И
так,
если
,
то ее координаты удовлетворяют уравнению
(20). Если
,
то векторы
и
некомпланарны, следовательно, координаты
точки
не удовлетворяют уравнению (20). Таким
образом, уравнение (20) есть уравнение
плоскости
.
Оно называется
уравнением плоскости, заданной точкой и двумя неколлинеарными векторами и .
2. Параметрическое уравнение плоскости.
Пусть , .
тогда и только
тогда, когда векторы
и
компланарны. По теореме о компланарных
векторах
.
Переходя к координатам, получаем:
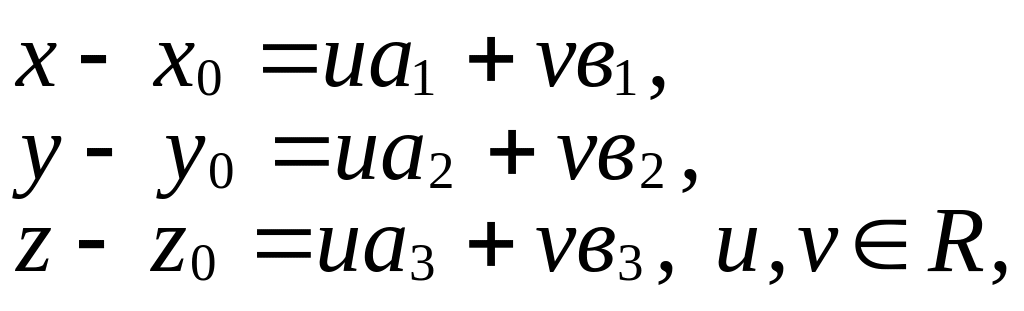или
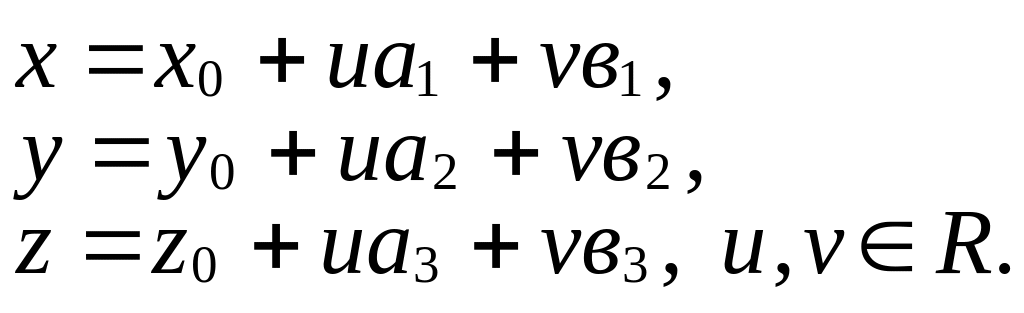(21)
Система уравнений (21) называется параметрическим уравнением плоскости.
Действительные числа u и v называются параметрами.
Геометрический
смысл
параметров u
и v:
для любой точки
существует единственная пара параметров
,
удовлетворяющих уравнениям (21), и обратно,
и
.
3. Уравнение плоскости, заданной тремя точками.
Пусть
не лежат на одной прямой,
,
,
.
Т
ак
как точки
,
и
не лежат на одной прямой, то
||
(рис. 66). Следовательно, плоскость
можно задать точкой
и двумя неколлинеарными векторами
и
:
.
Применяя уравнение (20), получаем:
.
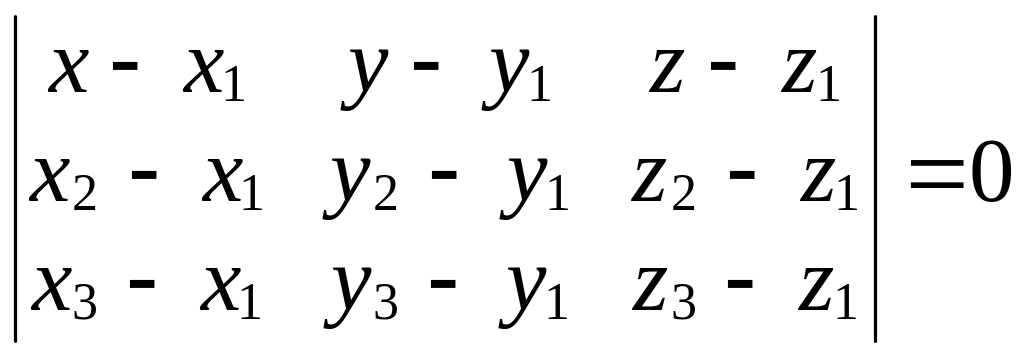(22)
Уравнение (22)
называется уравнением
плоскости, заданной тремя точками
.
4. Уравнение плоскости «в отрезках».
Пусть
,
,
(рис. 67), где
.
Используя уравнение (22), получим:
;
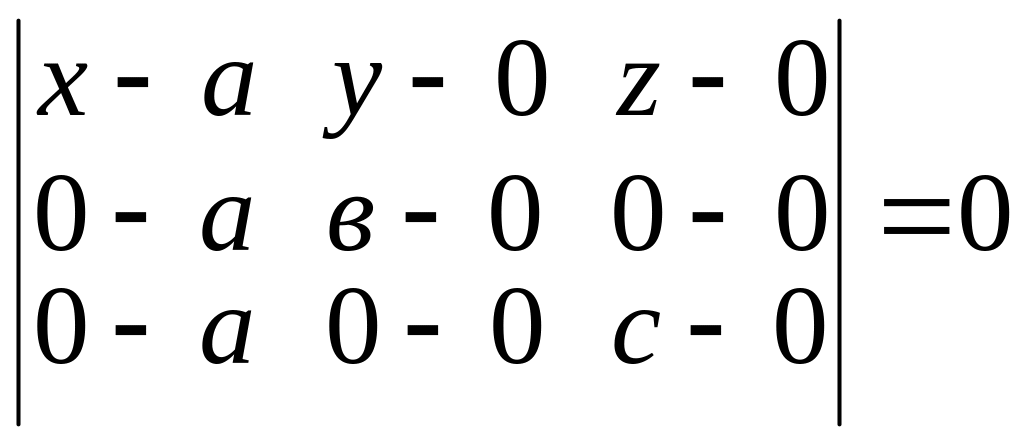т.е.
.
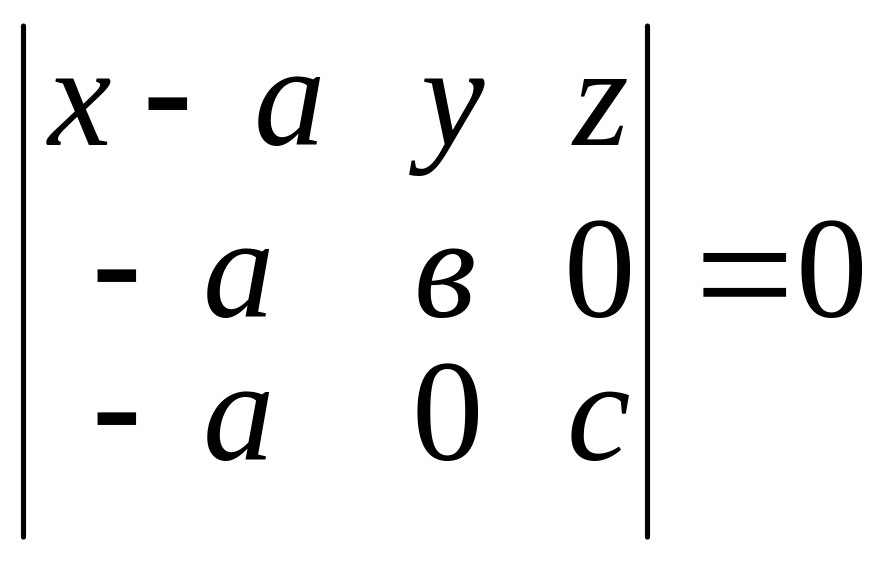Раскроем определитель, стоящий в левой части, и преобразуем это выражение:
;
;
разделим обе части этого уравнения на
:
,
откуда получаем уравнение:
.
(23)
Уравнение (23) называется уравнением плоскости «в отрезках».
Геометрический
смысл а,
в и
с: а
– это абсцисса точки пересечения
плоскости
с осью
,
в
– ордината точки пересечения
с осью
,
с
аппликата точки пересечения
с осью
аффинной системы координат.
Задания для самостоятельной работы
Найдите уравнения координатных плоскостей
аффинной системы координат
.Могут ли числа а, в и с в уравнении плоскости «в отрезках» быть равными нулю одновременно? Почему? Может ли только одно (или два) равняться 0? Почему?
Какое из следующих уравнений является уравнением плоскости «в отрезках», а какое – не является и почему? Как привести его к виду «в отрезках»?
а)
|
в)
|
б)
|
г)
|
;
;
;
.
Можно ли пользоваться уравнениями плоскости (20)-(23) в прямоугольной декартовой системе координат и почему?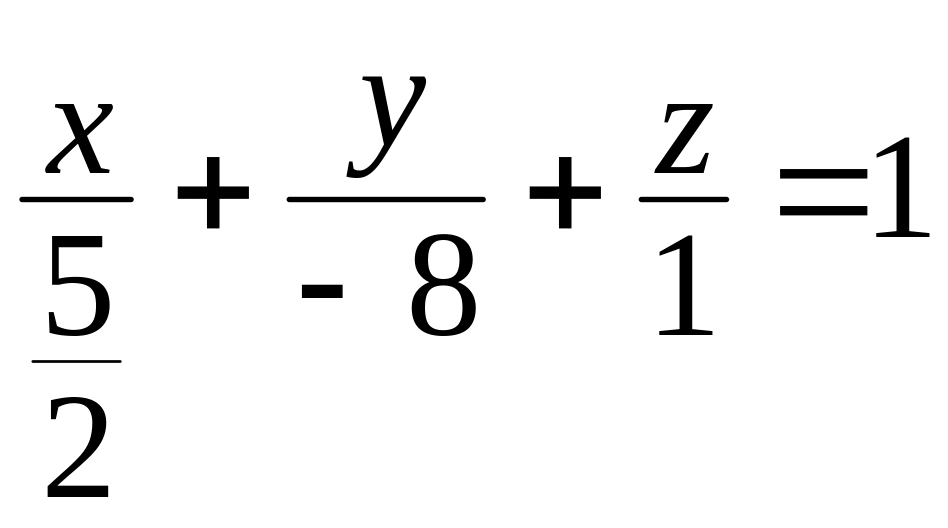