
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •§4. Линейная зависимость векторов и ее свойства
- •Примеры
- •Свойства линейно зависимой системы векторов
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •§8. Векторное произведение двух векторов
- •Геометрические свойства векторного умножения векторов
- •Алгебраические свойства векторного умножения векторов
- •Применение векторного произведения
- •Задания для самостоятельной работы
- •§9. Смешанное произведение трех векторов
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения трех векторов
- •§10. Понятие аффинной и прямоугольной декартовой
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Прямая линия на плоскости Лекция 9 Прямая в аффинной системе координат
- •§15. Различные уравнения прямой
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •§18. Уравнение прямой, заданной точкой и
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •§20. Различные уравнения плоскости
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§22. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§23. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§24. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§25. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§26. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
Глазовский государственный педагогический институт
им. В.Г. Короленко
Кафедра алгебры, геометрии, теории и методики обучения математике
Конспекты лекций
по аналитической геометрии
(для студентов первого курса математического факультета)
Глазов 2006
Лекции по геометрии
для студентов математического факультета
Автор: зав. кафедрой алгебры, геометрии, теории и методики обучения математике, канд. физ.-мат. наук, доцент Л.Т. Крежевских
Методические рекомендации по работе
с электронным вариантом лекций
В начале первой лекции преподаватель знакомит студентов с последовательностью работы с электронным вариантом лекций. Работа с электронными методическими материалами – это один из видов самостоятельной работы студентов. При подготовке к лекциям можно заниматься в компьютерном классе, но наиболее удобно иметь все конспекты лекций в распечатанном виде и заниматься по ним (при подготовке к лекциям, практическим занятиям, контрольным работам, экзаменам). Распечатанные конспекты лекций нужно всегда приносить на лекции и на практические занятия.
Внимание! Наличие электронного варианта лекций не освобождает студента от обязательного посещения всех лекций и практических занятий!
При подготовке к каждой лекции, начиная со второй, студент выполняет следующую работу с конспектами лекций и с электронными материалами:
Повторяет материал предыдущей лекции и отвечает на вопросы, сформулированные в конце каждого параграфа.
Внимательно читает материал предстоящей лекции.
Таким образом, на лекцию он приходит подготовленным к восприятию нового материала.
На каждой лекции преподаватель формулирует все необходимые определения, свойства, теоремы, сопровождая их чертежами и пояснениями. Если доказательство теоремы или свойства не сложное, то дает схему этого доказательства. Подробно студент изучает доказательство самостоятельно. Если доказательство может вызвать трудности у студента, преподаватель останавливается на наиболее сложных моментах.
По ходу лекции преподаватель дает рекомендации по практическому приложению теории к решению геометрических задач, по подготовке к практическому занятию по данной теме, по использованию электронных методических материалов, учебников, методических пособий и другой литературы.
При подготовке к практическому занятию студенту необходимо выучить все определения, формулы, формулировки свойств и теорем по теме занятия, понять их геометрический смысл, выполнить пункты 1, 2, 3 из «Методических рекомендаций по подготовке к практическим занятиям», а также решить задачи из пункта 6 указанных рекомендаций по теме предыдущего занятия.
Отдельные темы преподаватель может вынести на самостоятельное изучение, дав на лекции или на практическом занятии лишь некоторые рекомендации.
Контроль за самостоятельной работой (КСР) студентов по изучению теории и ее применению к решению задач осуществляется на специальных занятиях по отдельному расписанию, составленному деканатом, а также на практических занятиях. Контроль может осуществляться в различных формах: в виде коллоквиумов в устной или письменной форме, математических диктантов, индивидуальных собеседований, контрольных работ, компьютерного тестирования.
Для занятий геометрией каждому студенту необходимо иметь:
Папку-файл (или папку-уголок) для хранения распечатанных текстов лекций.
Общую тетрадь для работы на лекциях по геометрии.
Общую тетрадь для практических занятий и домашних заданий (домашнее задание по каждой теме должно быть оформлено сразу после практического задания, а не в конце тетради!).
Тонкую тетрадь для контрольных работ.
Хорошо отточенный карандаш средней мягкости.
Линейку.
Циркуль.
Ластик.
Цветную пасту, карандаши или тонкие фломастеры.
Бумагу для черновиков (любую).
Авторучку с синей (или черной) пастой.
На каждую лекцию необходимо приносить все, что указано в пунктах 1), 2), 5)-9), 11).
На каждое практическое занятие необходимо приносить все, что указано в пунктах 1)-11), а также:
Учебную программу по геометрии для студентов по специальности «Математика и информатика».
Методические рекомендации по подготовке к практическим занятиям по курсу «Геометрия». Часть 1, 2. Аналитическая геометрия. – Глазов, 1995.
Индивидуальные задания по аналитической геометрии. Для студентов 1 курса математического факультета. – Глазов, 2003.
Список рекомендуемой литературы
Атанасян Л.С., Базылев В.Т. Геометрия. В 2-х частях. Часть 1. – М.: Просвещение, 1986.
Атанасян Л.С. Геометрия. Часть 1. – М.: Просвещение, 1973.
Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии. Часть 1. – М.: Просвещение, 1973.
Базылев В.Т., Дуничев К.И., Иваницкая В.П. Геометрия. Часть 1. – М.: Просвещение, 1974.
Базылев В.Т. и др. Сборник задач по геометрии. – М.: Просвещение, 1980.
Аргунов Б.И., Демидова И.Н., Литвиненко В.Н. Задачник-практикум по геометрии. Часть 1 (для заочников). – М., 1979.
Бакельман И.Я. Аналитическая геометрия и линейная алгебра. – М.: Просвещение, 1976.
Бахвалов С.В. и др. Аналитическая геометрия. – М.: Просвещение, 1970.
Григорьев В.П., Дубинский Ю.А. Элементы высшей математики. – М., 2004.
Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель –АСТ, 2003.
Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Физматлит, 2002.
Индивидуальные задания по аналитической геометрии (для студентов математического факультета). – Глазов, 2003.
Методические рекомендации по подготовке к практическим занятиям по курсу «Геометрия». Часть 1, 2 (Аналитическая геометрия). – Глазов, 1995.
Погорелов А.В. Аналитическая геометрия. – М.: Наука, 1968.
Погорелов А.В. Геометрия. – М.: Наука, 1984.
Привалов И.И. Аналитическая геометрия. – М.: Государственное издательство физико-математической литературы, 1962.
Руководство к решению задач по высшей математике. Часть 1. Под общей ред. Е.И. Гурского. – Минск, 1989.
Учебная программа по дисциплине «Геометрия» для студентов по специальности «Математика» с дополнительной специальностью «Информатика». – Глазов, 2003.
Линейная алгебра и аналитическая геометрия: пособие к практическим занятиям для студентов факультета социальных и информационных технологий. – Глазов: Изд. центр ГГПИ, 2005.
Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
§1. Понятие вектора
Направленным
отрезком
называется отрезок, у которого указаны
начало и конец. Обозначение:
![]()
Вектором
называется направленный отрезок.
Обозначение:
![]() (рис. 1).
(рис. 1).
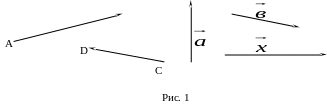
Вектор называется
нулевым,
если его начало и конец совпадают.
Обозначение:
![]() .
.
Векторы
![]() и
и
![]() называются сонаправленными
(противоположно направленными),
если лучи [AB)
и [CD)
сонаправлены (противоположно направлены).
Обозначение:
называются сонаправленными
(противоположно направленными),
если лучи [AB)
и [CD)
сонаправлены (противоположно направлены).
Обозначение:
![]() (
(![]() ).
).
На рис. 2
,
![]() .
.

Векторы
![]() и
и
![]() называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Обозначение:
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Обозначение:
![]() ||
||![]() .
.
Нулевой вектор считается коллинеарным любому вектору.
Векторы
![]() и
и
![]() называются компланарными,
если существует плоскость, которой они
параллельны.
называются компланарными,
если существует плоскость, которой они
параллельны.
Длиной
вектора называется расстояние между
его началом и концом. Обозначение длины
вектора
:
![]() .
.
Длина нулевого
вектора равна 0, т.е.
![]() .
.
Вектор называется единичным, если его длина равна единице.
В пространстве существует бесконечное множество единичных векторов.
Два вектора
называются равными,
если они сонаправлены и длины их равны.
Обозначение:
![]() .
.
Два вектора называются противоположными, если они противоположно направлены и длины их равны.
Вектор, противоположный
вектору
,
обозначается
![]() .
.
Откладыванием
вектора
![]() от точки А
называется
процесс построения такой точки М,
что
от точки А
называется
процесс построения такой точки М,
что
![]() .
.
А
В


![]() ,
исходящий из точки А
и сонаправленный с вектором
(рис. 3). Затем на луче
откладывают с помощью циркуля отрезок
АМ, длина
которого равна длине вектора
.
Вектор
,
исходящий из точки А
и сонаправленный с вектором
(рис. 3). Затем на луче
откладывают с помощью циркуля отрезок
АМ, длина
которого равна длине вектора
.
Вектор
![]()
искомый, т.е.
.
искомый, т.е.
.
М


А![]()
Рис. 3
