
- •Список рекомендуемой литературы
- •Элементы векторной алгебры Лекция 1 Векторы. Линейные операции над векторами
- •§1. Понятие вектора
- •Задания для самостоятельной работы
- •§2. Сложение и вычитание векторов
- •Правило треугольника
- •Правило параллелограмма
- •Правило многоугольника
- •Правило построения разности двух векторов
- •Задания для самостоятельной работы
- •§3. Умножение вектора на число
- •§4. Линейная зависимость векторов и ее свойства
- •Примеры
- •Свойства линейно зависимой системы векторов
- •Задания для самостоятельной работы
- •Лекция 3 Базис. Координаты вектора
- •§5. Базис. Координаты вектора в данном базисе
- •И их свойства
- •Свойства координат векторов
- •Задания для самостоятельной работы
- •Лекция 4 Нелинейные операции над векторами
- •§6. Скалярное произведение двух векторов
- •Геометрические свойства скалярного умножения векторов
- •Алгебраические свойства скалярного умножения векторов
- •Приложение скалярного произведения векторов к доказательству теорем
- •Задания для самостоятельной работы
- •Лекция 5 Нелинейные операции над векторами
- •§7. Понятие об ориентации пространства и плоскости
- •Задания для самостоятельной работы
- •§8. Векторное произведение двух векторов
- •Геометрические свойства векторного умножения векторов
- •Алгебраические свойства векторного умножения векторов
- •Применение векторного произведения
- •Задания для самостоятельной работы
- •§9. Смешанное произведение трех векторов
- •Алгебраические свойства смешанного умножения векторов
- •Применение смешанного произведения трех векторов
- •§10. Понятие аффинной и прямоугольной декартовой
- •Задания для самостоятельной работы
- •§11. Основные аффинные и метрические задачи
- •Основные аффинные задачи
- •Основная метрическая задача
- •Задания для самостоятельной работы
- •Лекция 8 Формулы преобразования координат
- •§12. Преобразование аффинной системы координат
- •Частные случаи преобразования аффинной системы координат
- •Задания для самостоятельной работы
- •§13. Понятие направленного угла между векторами. Преобразование прямоугольной системы координат
- •Частные случаи преобразования прямоугольной системы координат
- •Задания для самостоятельной работы
- •§14. Полярные координаты
- •Задания для самостоятельной работы
- •Прямая линия на плоскости Лекция 9 Прямая в аффинной системе координат
- •§15. Различные уравнения прямой
- •Задания для самостоятельной работы
- •§16. Общее уравнение прямой и его частные случаи
- •Частные случаи общего уравнения прямой
- •Задания для самостоятельной работы
- •§17. Основные аффинные задачи, связанные с прямой на плоскости (обзор)
- •Задания для самостоятельной работы
- •§18. Уравнение прямой, заданной точкой и
- •Задания для самостоятельной работы
- •§19. Основные метрические задачи, связанные с прямой на плоскости
- •§20. Различные уравнения плоскости
- •Задания для самостоятельной работы
- •§21. Общее уравнение плоскости
- •Задания для самостоятельной работы
- •§22. Основные аффинные задачи, связанные с плоскостью (обзор)
- •Задания для самостоятельной работы
- •Лекция 12 Плоскость в прямоугольной системе координат
- •§23. Основные метрические задачи, связанные с плоскостью
- •Задания для самостоятельной работы
- •Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
- •§24. Различные уравнения прямой в пространстве
- •Задания для самостоятельной работы
- •§25. Основные аффинные задачи на прямые и плоскости
- •Задания для самостоятельной работы
- •§26. Основные метрические задачи на прямые и плоскости в пространстве
- •Задания для самостоятельной работы
§21. Общее уравнение плоскости
Теорема 1.
Плоскость есть поверхность первого
порядка, т.е. задается в аффинной системе
координат уравнением первой степени
![]() ,
где
,
где
![]() не равны нулю одновременно. Обратно,
поверхность в пространстве, заданная
в аффинной системе координат уравнением
первой степени
(где
не равны нулю одновременно), есть
плоскость.
не равны нулю одновременно. Обратно,
поверхность в пространстве, заданная
в аффинной системе координат уравнением
первой степени
(где
не равны нулю одновременно), есть
плоскость.
□ Пусть плоскость
задана точкой
![]() и двумя неколлинеарными векторами
и двумя неколлинеарными векторами
![]() и
и
![]() ,
т.е.
.
Найдем ее уравнение.
,
т.е.
.
Найдем ее уравнение.
 ;
;
![]() ;
;
![]() .
.
Положим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
Так как векторы
и
неколлинеарны, то их соответствующие
координаты не пропорциональны,
следовательно,
![]() ,
,
![]() и
и
![]() одновременно, т.е.
одновременно, т.е.
![]() одновременно.
одновременно.
Докажем обратное
утверждение. Пусть некоторая поверхность
![]() задана уравнением
,
где
не равны нулю одновременно. Докажем,
что
плоскость.
задана уравнением
,
где
не равны нулю одновременно. Докажем,
что
плоскость.
Пусть для
определенности
![]() .
Найдем уравнение плоскости
,
заданной точкой
.
Найдем уравнение плоскости
,
заданной точкой
![]() и двумя неколлинеарными векторами
и двумя неколлинеарными векторами
![]() и
и
![]() .
.
 ;
;
![]() ;
;
![]() ;
разделив обе части полученного уравнения
на
,
получим:
;
разделив обе части полученного уравнения
на
,
получим:
.
Итак, уравнение поверхности в точности совпадает с уравнением плоскости , следовательно, совпадает с , т.е. плоскость.
Если
![]() ,
то
,
то
![]() или
или
![]() .
Аналогичными рассуждениями убеждаемся,
что
плоскость. ■
.
Аналогичными рассуждениями убеждаемся,
что
плоскость. ■
Уравнение (где не равны нулю одновременно) называется общим уравнением плоскости. Переменные х, у, z называются текущими координатами произвольной точки плоскости.
Задания для самостоятельной работы
Можно ли пользоваться общим уравнением плоскости в прямоугольной декартовой системе координат и почему?
Выведите в аффинной системе координат уравнение
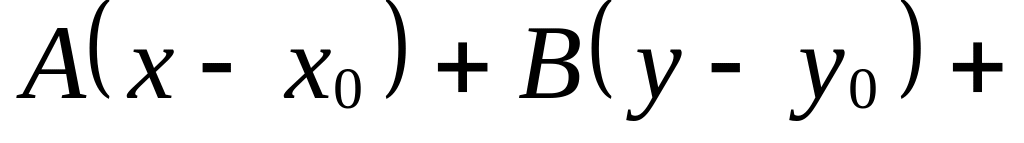
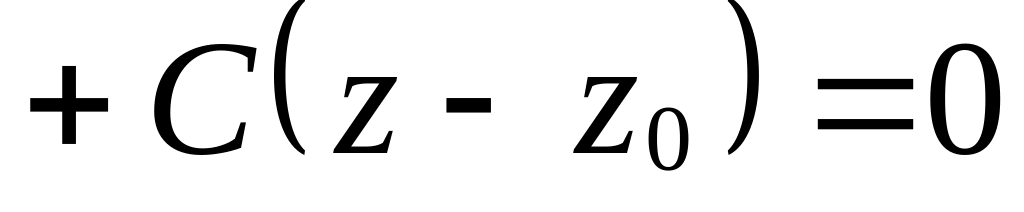 плоскости, проходящей через точку
.
плоскости, проходящей через точку
.Дано общее уравнение плоскости , в котором все коэффициенты при х, у и z и свободный член отличны от нуля. Получите из него уравнение плоскости «в отрезках».
Дано параметрическое уравнение плоскости. Получите из него общее уравнение плоскости.
Дано общее уравнение плоскости. Получите из него параметрическое уравнение плоскости.
Какая поверхность в пространстве задается в аффинной системе координат уравнением: а)
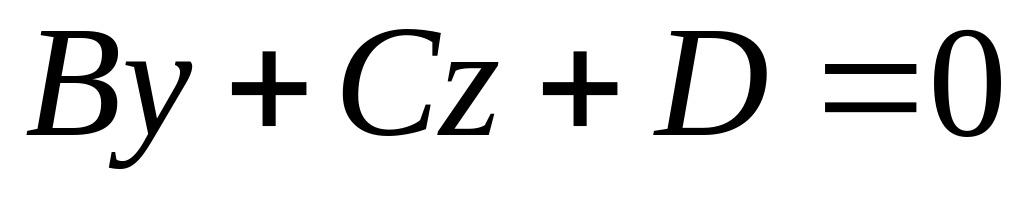 ;
б)
;
б)
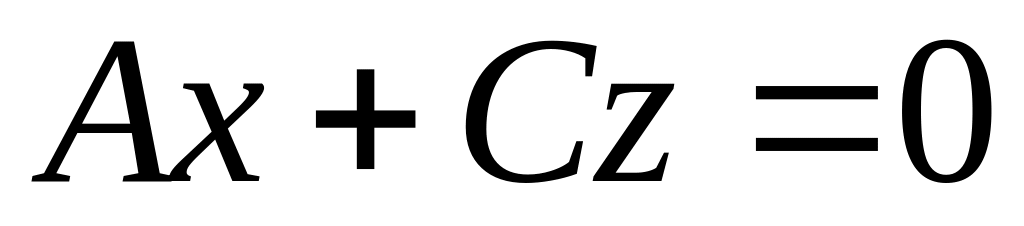 ;
в)
;
в)
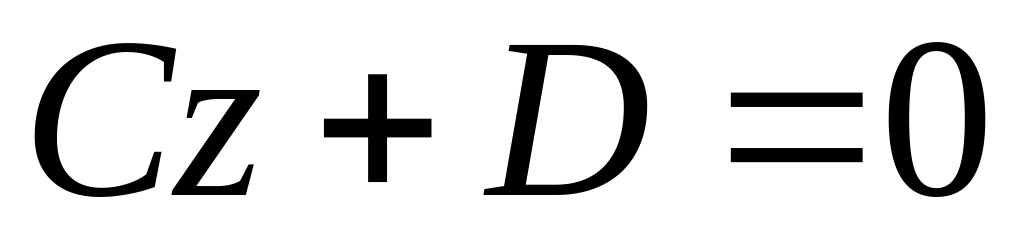 ;
г)
;
г)
 ;
д)
;
д)
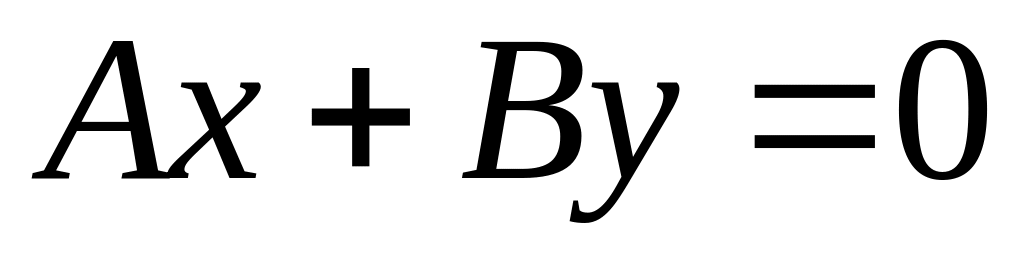 ?
?
§22. Основные аффинные задачи, связанные с плоскостью (обзор)
1. Взаимное расположение двух плоскостей.
Выяснить взаимное расположение двух плоскостей позволяет следующая теорема:
Теорема 1.
Пусть в аффинной системе координат
плоскости
![]() и
и
![]() заданы общими уравнениями:
заданы общими уравнениями:
![]() ,
,
![]() .
.
![]() или
или
![]() ;
;
![]() (коэффициенты при
х,
у,
z
пропорциональны, а свободные члены им
не пропорциональны);
(коэффициенты при
х,
у,
z
пропорциональны, а свободные члены им
не пропорциональны);
![]() .
.
2. Взаимное расположение трех плоскостей.
Вопрос о взаимном
расположении трех плоскостей
,
и
![]() сводится к исследованию вопроса о
взаимном расположении трех пар плоскостей:
и
,
и
,
и
.
сводится к исследованию вопроса о
взаимном расположении трех пар плоскостей:
и
,
и
,
и
.
Возможны восемь случаев взаимного расположения этих плоскостей:
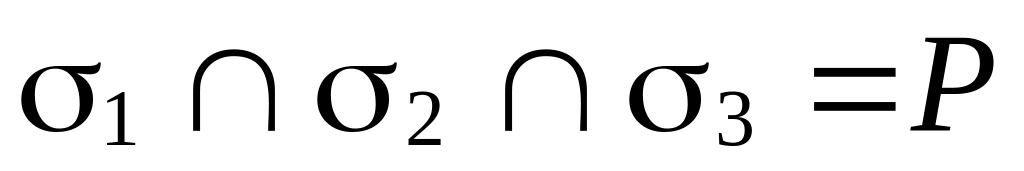 (рис. 69, а);
(рис. 69, а);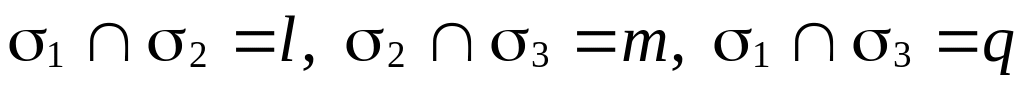 (рис. 69, б);
(рис. 69, б);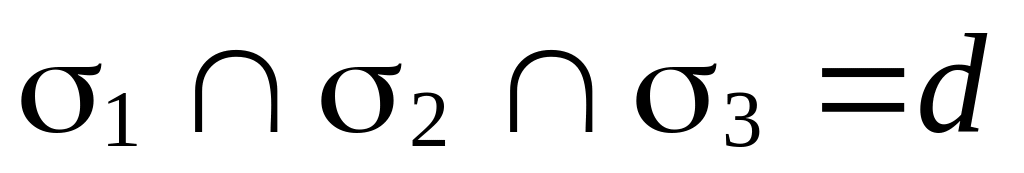 (рис. 69, в);
(рис. 69, в);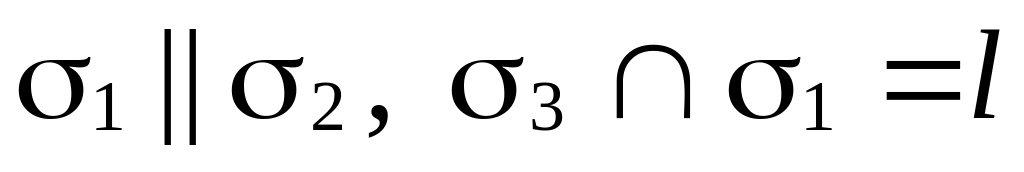 (следовательно,
(следовательно,
 )
(рис. 69, г);
)
(рис. 69, г);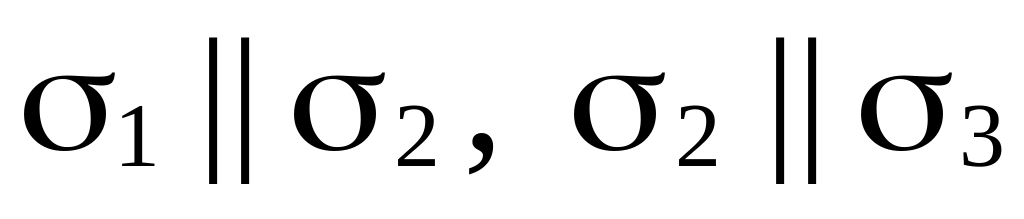 (следовательно,
(следовательно,
 )
(рис. 69, д);
)
(рис. 69, д);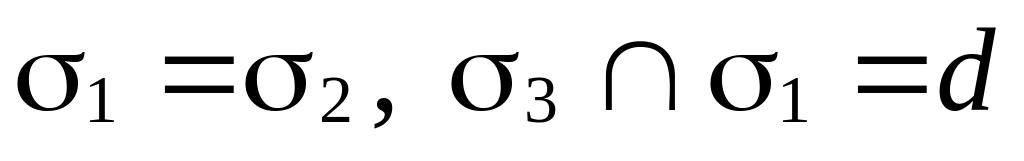 (рис. 69, е);
(рис. 69, е);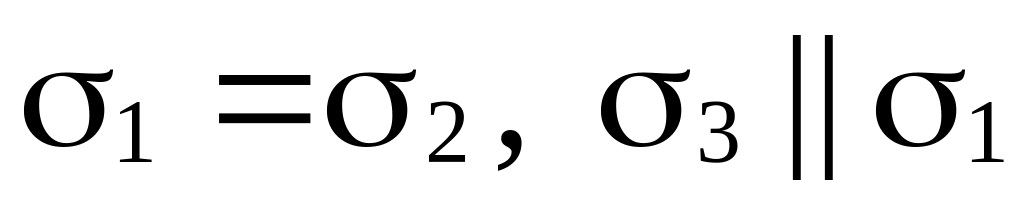
 (рис. 69, ж);
(рис. 69, ж);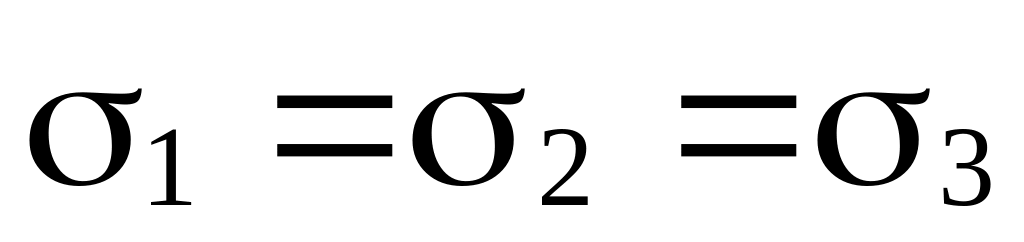 (рис. 69, з).
(рис. 69, з).

3. Геометрический
смысл знака многочлена
![]() .
.
Теорема 2.
Если в аффинной системе координат
плоскость
задана уравнением
![]() ,
то два полупространства, на которые эта
плоскость разбивает пространство,
определяются условиями
,
то два полупространства, на которые эта
плоскость разбивает пространство,
определяются условиями
![]() и
и
![]() .
.
4. Пучок и связка плоскостей.
Пучком плоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую . Прямая называется осью этого пучка.
Пусть
![]() .
Тогда уравнение пучка плоскостей с осью
имеет вид:
.
Тогда уравнение пучка плоскостей с осью
имеет вид:
![]() ,
где
,
где
![]() не равны нулю одновременно.
не равны нулю одновременно.
Связкой плоскостей называется множество всех плоскостей, проходящих через одну и ту же точку . Точка называется центром связки.
Пусть
![]() .
Тогда уравнение связки плоскостей имеет
вид:
.
Тогда уравнение связки плоскостей имеет
вид:
![]() ,
где
,
где
![]() и
не равны нулю одновременно.
и
не равны нулю одновременно.
