Задания для самостоятельной работы
Можно ли в аффинной системе координат пользоваться уравнением (27) и почему?
Выведите уравнение плоскости, проходящей через точку и перпендикулярной каждой из плоскостей и , уравнения которых даны в прямоугольной системе координат.
Докажите, что уравнение плоскости, проходящей через точки и перпендикулярно к плоскости
,
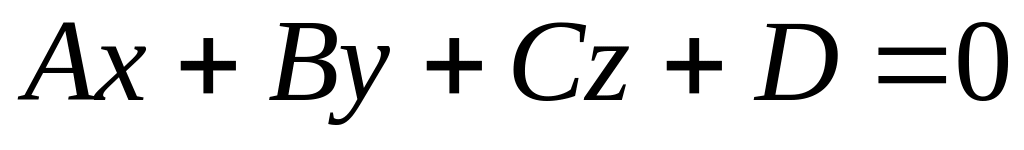может быть представлено в следующем
виде:
.
Пользуясь уравнением (27), найдите уравнения координатных плоскостей
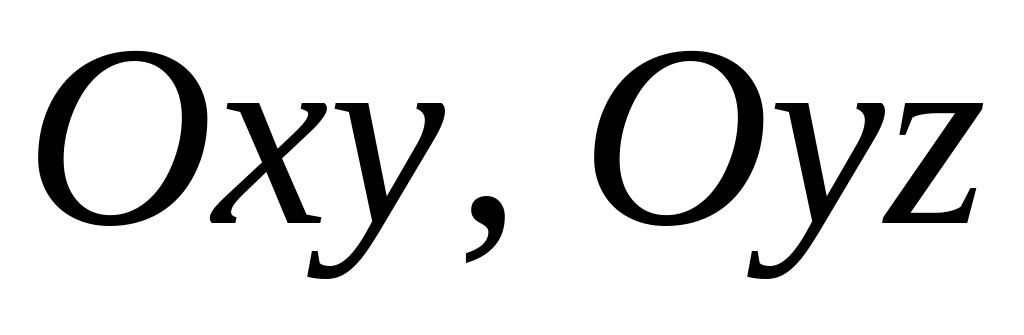и
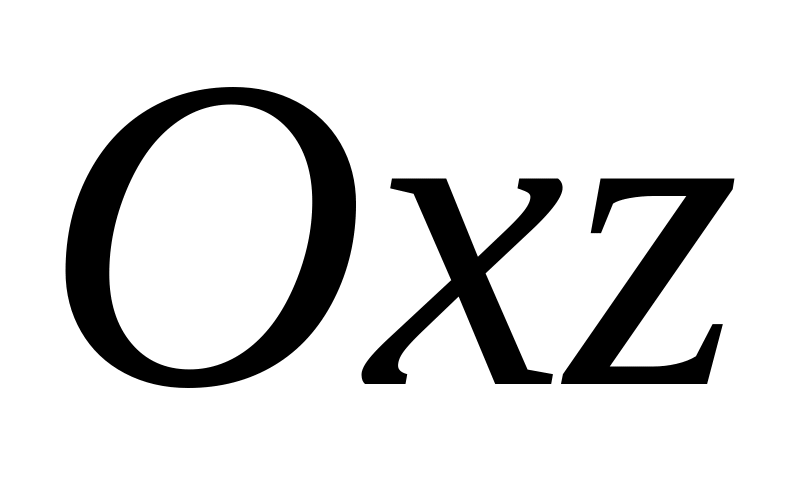прямоугольной
декартовой системы координат
.Найдите объем куба, одна грань которого принадлежит координатной плоскости , а другая – плоскости
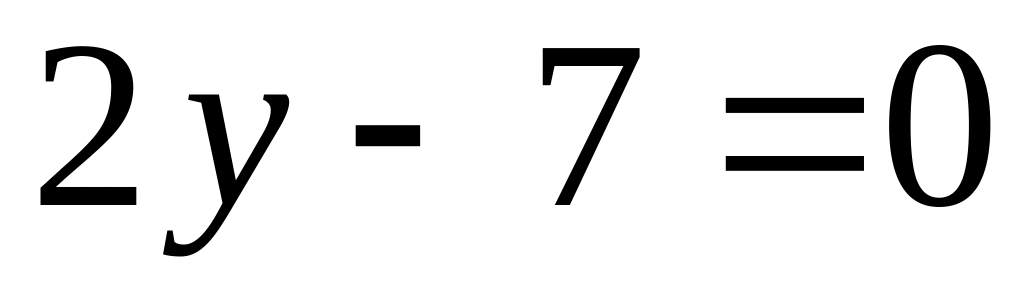.Вычислите косинусы углов, которые образует с координатными плоскостями прямоугольной декартовой системы координат плоскость .
Лекция 13 Прямая в пространстве. Различные задачи на прямые и плоскости в пространстве
§24. Различные уравнения прямой в пространстве
Положение прямой в пространстве определяется полностью, если даны:
а) две ее точки;
б) точка и направляющий вектор;
в) две плоскости, пересекающиеся по этой прямой.
Пусть в пространстве выбрана аффинная система координат .
1. Каноническое уравнение прямой.
П
усть
прямая
задана в пространстве точкой
и направляющим вектором
(рис. 73).
.
Далее применяем условие коллинеарности двух векторов в пространстве в координатах (см. § 5). При этом возможны различные случаи:
а)
и
.
Тогда получаем следующее уравнение
прямой:
.
(28)
б)
.
(29)
в)
(запишите уравнение прямой
самостоятельно).
г)
(запишите уравнение прямой
самостоятельно).
д)
.
Получаем следующее уравнение прямой
:
(30)
е)
(запишите уравнение прямой
самостоятельно).
ж)
(запишите уравнение прямой
самостоятельно).
Уравнения (28)-(30) (а также уравнения, записанные вами в пунктах в), г), е) и ж)) называются каноническими уравнениями прямой в пространстве.
2. Уравнение прямой, заданной двумя точками.
Пусть
.
Тогда прямую
можно задать точкой
и направляющим вектором
.
Поэтому применяем каноническое уравнение
прямой:
.
(31)
Уравнение (31) называется уравнением прямой в пространстве, заданной двумя точками.
Если одна или две координаты вектора окажутся нулевыми, то применяем частные случаи канонического уравнения прямой, т.е. уравнения вида (29) или (30).
3. Параметрическое уравнение прямой.
В случае, когда
прямая
задана так же, как в пункте 1 (точкой
и направляющим вектором
),
можно получить параметрическое уравнение
прямой.
(по теореме о коллинеарных векторах).
Переходя к координатам, получаем:
откуда
(32)
Система уравнений (32) называется параметрическим уравнением прямой в пространстве.
Действительное число в системе (32) называется параметром и имеет такой же смысл, как и параметр в параметрическом уравнении прямой на плоскости (см. § 15).
4
.
Уравнение
прямой, заданной двумя пересекающимися
плоскостями.
Пусть
в
(рис. 74).
Точка
тогда и только тогда, когда ее координаты
являются решением системы уравнений
плоскостей
и
.
Система уравнений
(33)
называется уравнением прямой, заданной двумя пересекающимися плоскостями.
Лемма 1. Вектор
(34)
является направляющим
вектором прямой
.
□ Воспользуемся дважды леммой о параллельности вектора и плоскости.
1) Докажем, что
.
.
Тогда по лемме о параллельности вектора
и плоскости
.
2) Докажите
самостоятельно, что
.
Из пунктов 1) и 2)
следует, что
,
т.е.
.
■
Итак, из леммы 1
следует, что если прямая
задана как линия пересечения двух
плоскостей
,
,
то координаты ее направляющего вектора
находятся по формуле (34).
Замечание.
Как и в случае прямой на плоскости,
переменные
в уравнениях (28)-(33) называются текущими
координатами точек прямой в пространстве.