Частные случаи преобразования прямоугольной системы координат

1. Перенос начала: , .

.

2. Поворот координатных векторов на угол : , .

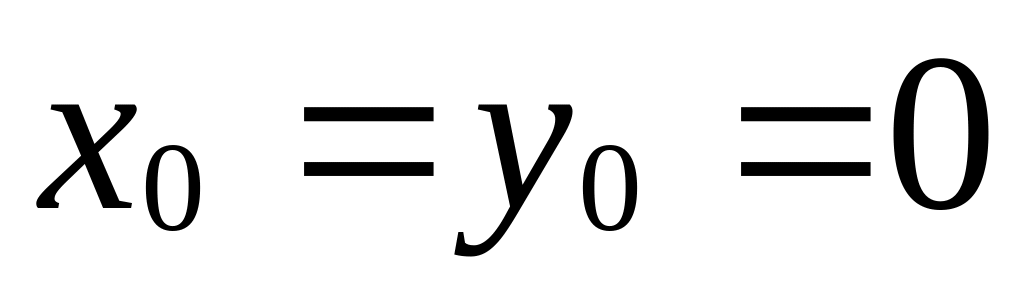Задания для самостоятельной работы

1. Определите (приближенно), чему равна величина направленного угла 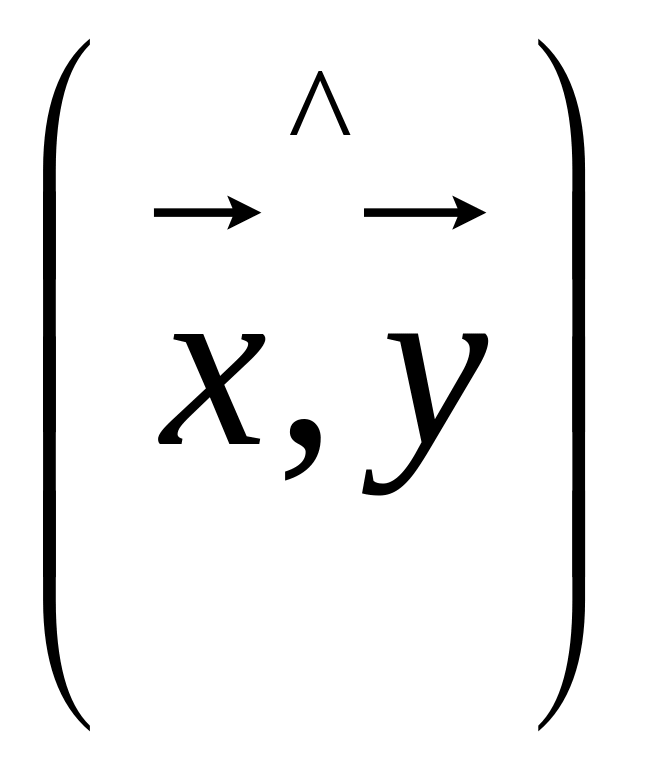(рис. 47, а, б).

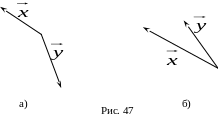
2. Может ли величина направленного угла между векторами быть равна 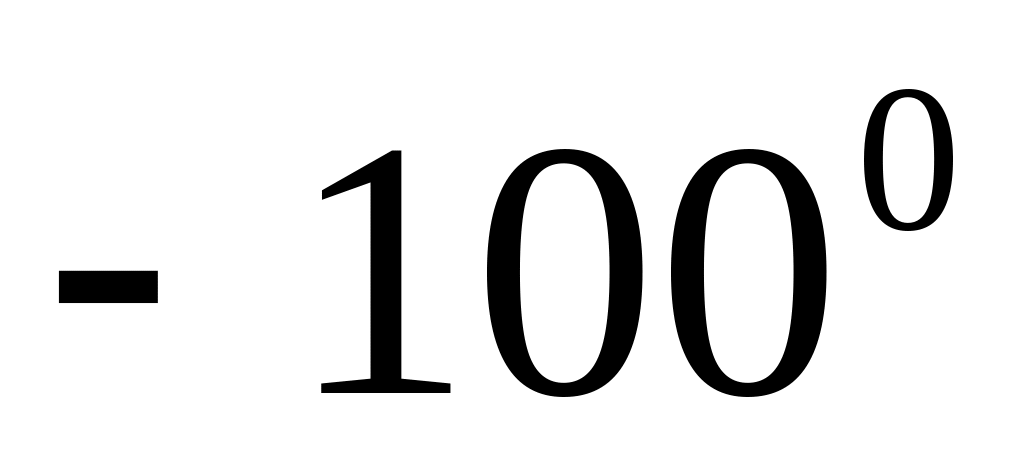? ? 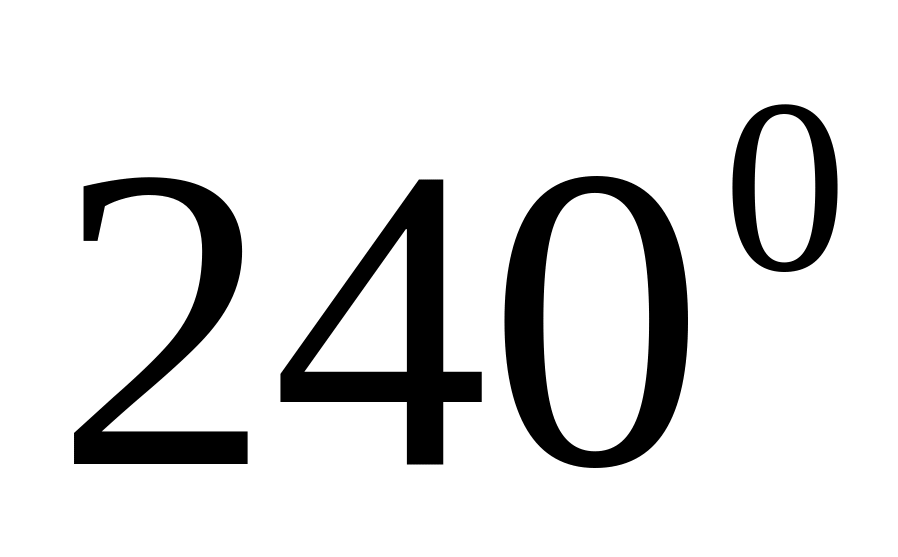? 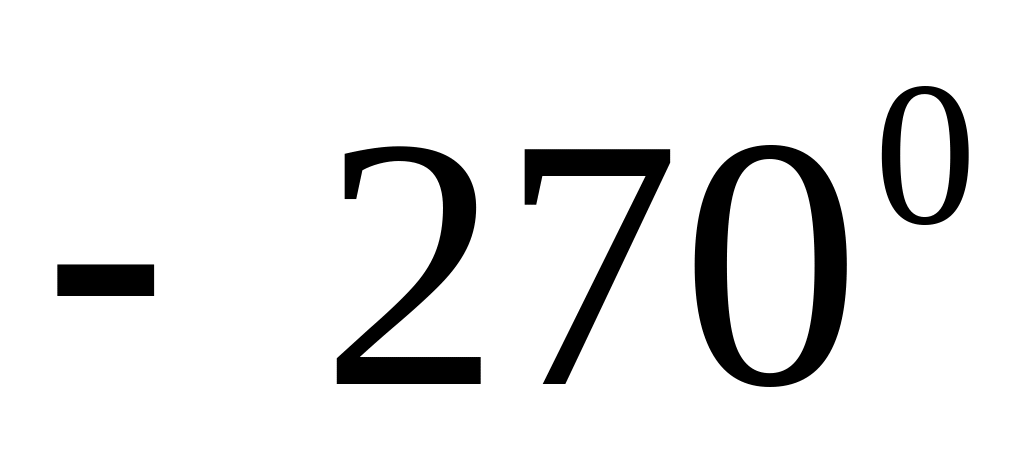Почему?

3. Найдите формулы преобразования прямоугольной системы координат, если координатные векторы повернуты на угол 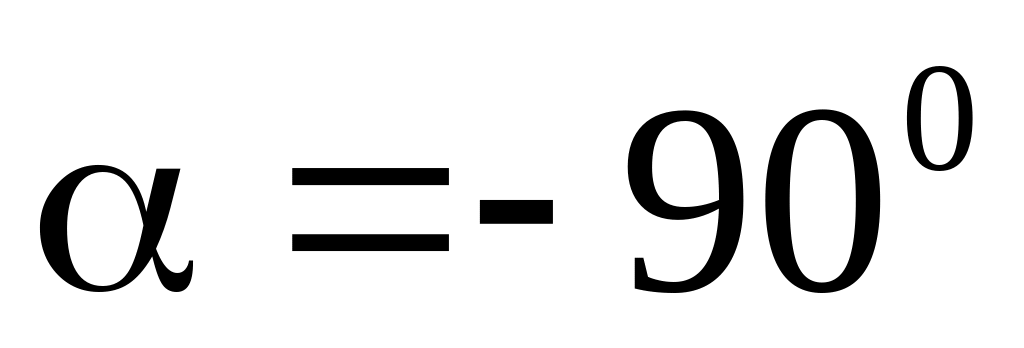, а начало координат перенесено в точку .

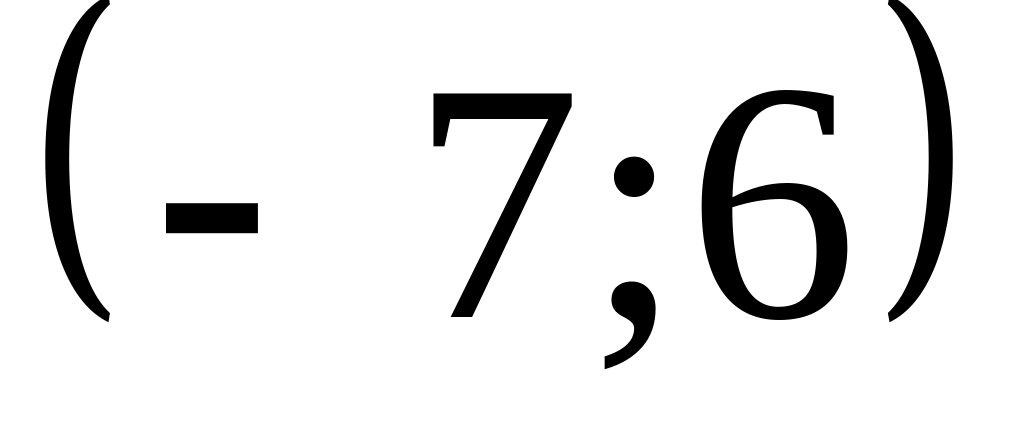4. Как по формулам преобразования координат узнать, какая система координат подвергается преобразованию: аффинная или прямоугольная?

5. Сделайте чертежи старой и новой систем координат для частных случаев преобразования прямоугольной декартовой системы координат.

§14. Полярные координаты

Если указано правило, по которому положение точек плоскости можно определить с помощью упорядоченных пар действительных чисел, то говорят, что на плоскости задана система координат. Кроме аффинной системы координат, которая была рассмотрена в §10, в математике часто применяют полярную систему координат на плоскости.

Система полярных координат вводится на ориентированной плоскости.

Пара, состоящая из точки О и единичного вектора , называется полярной системой координат и обозначается или . Направленная прямая называется полярной осью, точка О - полюсом (рис. 48).

П

О

усть М – произвольная точка плоскости. Расстояние от точки О до точки М называется полярным радиусом точки М.

.

Таким образом, . Если М совпадает с О, то . Для любой точки М ее полярный радиус

Н аправленный угол называется полярным углом точки М (рис. 49).

.

Если М совпадает с полюсом О, то  - неопределенный. Из определения направленного угла между векторами (см. §13) следует, что полярный угол

П олярный радиус  и полярный угол  называются полярными координатами точки М.

На рис. 50 построены точки , , по их полярным координатам.

Выведем формулы перехода от полярных координат к прямоугольным декартовым и обратно.

Пусть - полярная система координат на ориентированной плоскости, , в . Присоединим к полярной системе единичный вектор , ортогональный вектору так, чтобы базис , был правым (рис. 51).

, .

Пусть М(х;у) в . Тогда ; (рис. 51).

Получили формулы перехода от полярных координат к прямоугольным:

Возведем обе части этих равенств в квадрат и сложим:

, откуда (корень берется со знаком «+», т.к. ).   ; .

, , .

Получили формулы перехода от прямоугольных декартовых координат к полярным:

З амечание. При решении задач на переход от прямоугольных декартовых координат к полярным недостаточно найти только или только , т.к. по одной тригонометрической функции определить полярный угол однозначно невозможно: в промежутке существуют два угла с одинаковыми косинусами (два угла с одинаковыми синусами) (рис. 52). Поэтому правильно найти полярный угол  вы сможете, только если одновременно вычислите и .