Простейшие следствия из аксиом

1°.

► : . С другой стороны, [1*] = На основании второй аксиомы получаем требуемое.◄

2°.

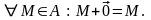
►Если содержит одну точку, то утверждение очевидно. Если же не одну, то ◄

3°.

 Но и . Поэтому на основании второй аксиомы получаем , что равносильно доказываемому утверждению. ◄

Если V – n-мерное линейное пространство, то связанное с ним аффинное пространство тоже называется n-мерным и обозначается .

Системой координат в аффинном пространстве называется совокупность точки – начала координат, и базиса линейного пространства .

Пусть в пространстве задана система координат

. (3.34)

Тогда каждой точке соответствует единственный вектор , который называется радиусом вектором точки М. Координатами точки М в системе координат (3.34) называются координаты ее радиуса вектора в базисе .

Выберем в две произвольные точки М и N. Имеем

. (3.35)

Так как координаты точки совпадают с координатами ее радиуса вектора, то из (3.35) получаем вывод, который звучит так же, как известное школьное утверждение: чтобы найти координаты вектора, следует от координат его конца отнять соответствующие координаты начала.

Вопрос 7

как пример аффинного, евклидова и метрического пространств

Важнейшим примером аффинного пространства является пространство . Положим

,

.

Для любых и определим операцию . Проверим выполнение аксиом:

;

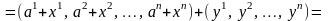
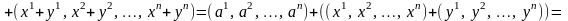
положим

.

Тогда

Предположим, что существует вектор такой, что . Пусть . Значит, . Так как , то и поэтому . Следовательно, – противоречие.

Таким образом, пространство с введенной в нем операцией откладывания вектора от точки становится n-мерным аффинным или точечным пространством. Упорядоченные наборы из чисел в зависимости от контекста рассматриваются либо как векторы, либо как точки, а операция складывания упорядоченных наборов, опять же в зависимости от контекста, рассматривается либо как сложение векторов, либо как откладывание вектора от точки.

В качестве системы координат в выбирают, как правило, следующую:

Эта система координат удобна тем, что в ней координаты точек и векторов совпадают с упорядоченными наборами, изображающими эти точки или векторы.

Введем в еще одну операцию. Скалярным произведением векторов и пространства назовем число

.

Свойства скалярного произведения

1.

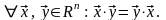
2.

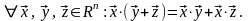
3.

4. причем

Свойства 1 – 4 вы легко докажете в качестве упражнения исходя из определения скалярного произведения в .

Пространство с введенной в нем операцией скалярного произведения называется евклидовым пространством (подробно категорию евклидовых пространств мы будем изучать в шестой главе).

Из свойства 4 скалярного произведения видно, что для любого вектора существует . Это позволяет ввести в понятие длины вектора.

Длиной вектора называется число .

Очевидно, если , то 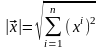, т. е., как и в школьной математике, длина вектора равна корню квадратному из суммы квадратов его координат.

Приведем без доказательства еще два свойства скалярного произведения (доказывать их будем в 6-й главе).

Неравенство Коши – Буняковского:

, или ;

неравенство треугольника:

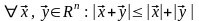, или .

Из неравенства Коши – Буняковского вытекает, что для всех ненулевых векторов пространства выполняется неравенство , что дает возможность ввести понятие угла между векторами.

Углом между ненулевыми векторами и пространства называется угол 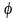такой, что

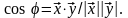
Введем еще в понятие расстояния между точками.

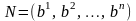Расстоянием между точками М и N в пространстве называется число . Если , а , то

.

Таким образом, как и в школьной математике, расстояние между двумя точками в пространстве равно корню квадратному из суммы квадратов разностей их соответствующих координат.