Вопрос 27

Определение и свойства собственных векторов

Собственные векторы линейного оператора

Определение. Ненулевой вектор линейного пространства V над полем P называется собственным вектором линейного оператора 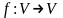, если существует такое числ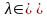о P, что

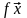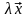= . (4.41)

Число 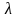из равенства (4.41) называется собственным значением оператора f, соответствующим собственному вектору .

Очевидно, все векторы линейного пространства являются собственными векторами нулевого оператора с собственным значением, равным 0, они же являются собственными векторами тождественного оператора с собственным значением, равным 1. Оператор проектирования трехмерного пространства на ось Оx имеет следующие собственные векторы: параллельные оси Оx – собственные с собственным значением, равным 1, а векторы, перпендикулярные оси Оx, – собственные с собственным значением, равным 0. При любом 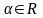функция является собственным вектором (или собственной функцией) оператора дифференцирования , причем собственное значение равно .

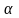Свойства собственных векторов

1º. Каждому собственному вектору соответствует единственное собственное значение.

► Предположим, что некоторому собственному вектору соответствуют два разных собственных значения и (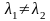 ). Тогда

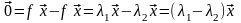. (4.42)

По шестому следствию § 1 гл. 3, из (4.42) следует, что , что противоречит определению собственного вектора.◄

2º. Собственные векторы с различными собственными значениями линейно независимы.

►Пусть , , …, – собственные векторы линейного оператора с собственными значениями соответственно, причем 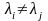при 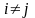. Доказательство проведем методом математической индукции по количеству векторов.

a) 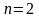. Предположим, что векторы линейно зависимы. Тогда один из них можно выразить через другой, например, . Имеем

,

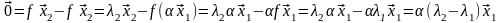откуда получаем, что (так как ,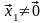 ), а значит, 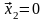, что противоречит определению собственного вектора.

б) Предположим, что утверждение справедливо для (n–1)-го вектора и докажем его справедливость для n векторов. Пусть собственные векторы 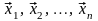с различными собственными значениями линейно зависимы. Значит, один из них можно представить в виде линейной комбинации остальных, например:

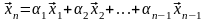. (4.43)

Так как 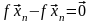, получаем

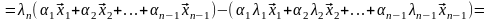
. (4.44)

По предположению индукции, векторы , , …, 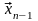линейно независимы. Поэтому из (4.44) вытекает, что , Так как , то при 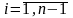. Но тогда из (4.43) видно, что 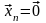, что противоречит определению собственного вектора.◄

3º. Множество всех собственных векторов линейного оператора с одним и тем же собственным значением вместе с нулевым вектором является подпространством линейного пространства V.

►Заметим, что состоит из всех векторов, удовлетворяющих условию (4.42), 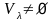т.к. при любом . Докажем замкнутость относительно операций, заданных в V. Действительно,

{ } { ; }

{ } { };

{ } { } { } { }.

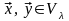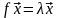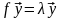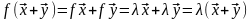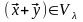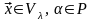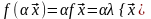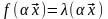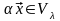На основании теоремы 3.4, – подпространство линейного пространства V.◄

4º. Пусть – линейный оператор, – его различные собственные значения. Обозначим

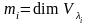и .

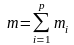Тогда в существует 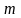линейно независимых собственных векторов оператора .

►В каждом из подпространств 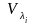выберем 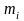линейно независимых векторов 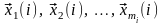и покажем, что система

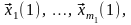
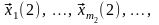
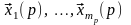– (4.45)

линейно независима. Для этого составим ее линейную комбинацию и приравняем :

. (4.46)

Обозначим 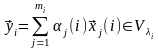. Тогда (4.46) примет вид

,

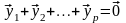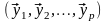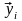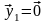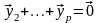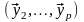откуда вытекает, что система линейно зависима. Поэтому на основании свойства 2º не все из векторов являются собственными, т. е. среди них есть нулевые. Пусть, например, . Это означает, что (объясните, почему), и что . Теперь видим, что система линейно зависима. Значит, и среди этих векторов есть нулевые. Пусть, например, 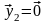со всеми вытекающими отсюда последствиями. 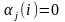После конечного числа шагов получаем, что в (4.46) все коэффициенты , откуда и следует линейная независимость системы (4.45).◄