
- •Коллоквиум по ла
- •Определение линейного пространства и простейшие следствия из аксиом
- •Примеры линейных пространств
- •Простейшие следствия из аксиом.
- •Вопрос 2 Линейная зависимость и независимость элементов линейного пространства
- •Примеры линейной зависимости и независимости
- •Простейшие свойства линейной зависимости
- •Вопрос 3 Базис и координаты в линейном пространстве
- •Примеры
- •Свойства координат векторов
- •Вопрос 4 Матричный критерий линейной зависимости и независимости
- •Вопрос 5 Размерность линейного пространства
- •Простейшие следствия из аксиом
- •Вопрос 7
- •Свойства скалярного произведения
- •Свойства расстояния
- •Вопрос 8 Подпространства линейного пространства
- •Вопрос 9 Линейные оболочки
- •Вопрос 10
- •Вопрос 11
- •Сумма и пересечение подпространств линейного пространства
- •Вопрос 12
- •Вопрос 13
- •Вопрос 14
- •Вопрос 15
- •Понятие отображения
- •Вопрос 16
- •Примеры линейных операторов
- •Простейшие свойства линейного оператора
- •Вопрос 17
- •Примеры
- •Связь координат вектора с координатами его образа
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Свойства изоморфизма
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Свойства собственных векторов
- •Вопрос 28
- •Правило нахождения собственных векторов
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32
- •Правило нахождения присоединенных векторов
- •Таким образом, имеем единственное собственное значение, кратность которого равна 3. Определим количество собственных и присоединенных векторов.
Вопрос 19
Операции над линейными операторами
Определения.
Пусть
 и
и
 – линейные пространства над одним и
тем же полем
.
– линейные пространства над одним и
тем же полем
.
Суммой линейных
операторов
и
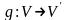 называется отображение
называется отображение
 такое, что
:
такое, что
:
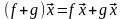 .
.
Произведением
линейного оператора
на число
называется отображение
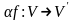 такое, что
:
такое, что
:
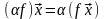 .
.
Произведением
линейных операторов
и
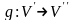 называется отображение
называется отображение
 такое, что
:
такое, что
:
 (т. е. произведение линейных операторов
– это просто произведение или композиция
отображений).
(т. е. произведение линейных операторов
– это просто произведение или композиция
отображений).
Теорема 4.3.
Сумма линейных операторов, произведение
линейного оператора на число и произведение
линейных операторов также являются
линейными операторами. При этом, если
 ,
А
и В
– матрицы линейных операторов f
и g
соответственно в некотором базисе
пространства
,
то матрицы операторов
,
А
и В
– матрицы линейных операторов f
и g
соответственно в некотором базисе
пространства
,
то матрицы операторов
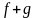 ,
,
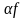 и gf
в том же базисе совпадают соответственно
с матрицами А
+ В, αА
и ВА.
и gf
в том же базисе совпадают соответственно
с матрицами А
+ В, αА
и ВА.
►Доказательство проведем для произведения линейных операторов.
Пусть и – линейные операторы. Тогда
 = [линейность f
] =
= [линейность f
] =
 =
=
=[
линейность g
] =
 =
=
 ;
;
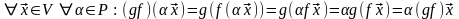 .
.
Таким образом, gf – линейный оператор.
Пусть
 – матрицы линейных операторов
и
– матрицы линейных операторов
и
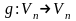 соответственно в базисе
соответственно в базисе
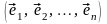 пространства
,
и пусть
пространства
,
и пусть
 – матрица оператора gf
в том же
базисе. Тогда по определению матрицы
линейного оператора
– матрица оператора gf
в том же
базисе. Тогда по определению матрицы
линейного оператора
 .
(4.25)
.
(4.25)
С другой стороны,
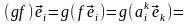 [линейность g]
=
[линейность g]
=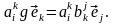 (4.26)
(4.26)
Сравнивая (4.25) и
(4.26), на основании единственности
координат вектора в данном базисе делаем
вывод:
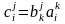 ,
откуда и получаем матричную запись: С
= ВА.◄
,
откуда и получаем матричную запись: С
= ВА.◄
Вопрос 20
Невырожденные линейные операторы. Теорема о матрице
Определение. Линейный оператор называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
Теорема 4.4. Для того чтобы линейный оператор был невырожденным необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом базисе пространства была невырожденной
►Пусть А – матрица линейного оператора в некотором базисе, Х, как обычно, координатный столбец вектора в том же базисе. Тогда
{f
– невырожденный}
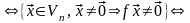
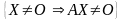 {однородная
система линейных уравнений AX
= O
имеет единственное тривиальное решение}
{
{однородная
система линейных уравнений AX
= O
имеет единственное тривиальное решение}
{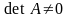 }.
}.
Так как определители подобных матриц совпадают, то утверждение справедливо и для любого базиса. ◄
Теорема 4.6. Произведение невырожденных линейных операторов – невырожденный линейный оператор.
►Пусть и – невырожденные линейные операторы. Тогда
{ }
{
}
{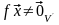 }
{
}
{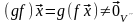 }.
}.
Tаким образом, gf – невырожденный линейный оператор.◄
Вопрос 21
Невырожденные линейные операторы. Теорема о взаимной однозначности
Определение. Линейный оператор называется невырожденным, если он любой ненулевой вектор переводит в ненулевой.
Теорема 4.4. Для того чтобы линейный оператор был невырожденным, необходимо и достаточно, чтобы он был взаимно однозначным.
►Пусть – линейный оператор, А – его матрица в некотором базисе, X и Y – координатные столбцы в том же базисе векторов и соответственно. Тогда
{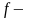 невырожденный}
невырожденный}
 {
{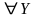 система
система
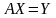 имеет единственное решение}
{
имеет единственное решение}
{
 единственный
,
что
}
единственный
,
что
}
{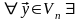 единственный
единственный
 ,
что
,
что
 }
{f
– взаимно однозначный}.◄
}
{f
– взаимно однозначный}.◄
Теорема 4.6. Произведение невырожденных линейных операторов – невырожденный линейный оператор.
►Пусть и – невырожденные линейные операторы. Тогда
{ } { } { }.
Tаким образом, gf – невырожденный линейный оператор.◄
