Вопрос 31

Определение приводимости квадратной матрицы к диагональному виду и вторая теорема о приводимости

Определение. Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица – диагональная.

Теорема 4.14. Для того чтобы квадратная матрица А n-го порядка приводилась к диагональному виду над полем Р, необходимо и достаточно, чтобы все ее характеристические числа принадлежали этому полю и для каждого из них выполнялось условие

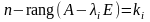, (4.58)

где 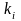– кратность корня характеристического уравнения матрицы А.

►Пусть – линейный оператор, построенный в теореме 4.13. На основании свойства 4º § 5 количество всех линейно независимых собственных векторов линейного оператора совпадает с суммой размерностей подпространств 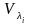по всем собственным значениям . Если это количество линейно независимых собственных векторов обозначить через m, то

.

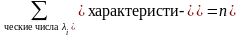Тогда

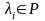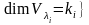
{А приводится к диагональному виду} {в существует базис из собственных векторов оператора f} {любое характеристическое число является собственным значением и 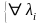} : и : и .◄

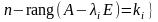Вопрос 32

Присоединенные векторы и правило их нахождения

Определение. Если – собственное значение линейного оператора , а система векторов 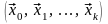пространства удовлетворяет условиям:

то вектор , называется i-м присоединенным вектором к собственному вектору линейного оператора .

Теорема 4.15. Пусть – линейное пространство над полем Р. Если все характеристические числа линейного оператора принадлежат полю Р, то в существует базис, состоящий из собственных и присоединенных векторов оператора f, причем каждому собственному значению в этом базисе соответствует столько собственных векторов и присоединенных к ним, какова кратность этого собственного значения (без доказательства).

Правило нахождения присоединенных векторов

Обозначим А матрицу линейного оператора в некотором базисе, – координатный столбец вектора 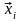в том же базисе. Тогда в матричном виде уравнение для нахождения будет выглядеть так:

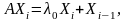
что равносильно уравнению

.

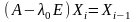Таким образом, видим, что для отыскания i-го присоединенного вектора к собственному вектору с собственным значением 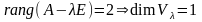следует решить систему линейных уравнений с той же матрицей, что и для отыскания собственного вектора , но неоднородную, причем в качестве столбца свободных членов берется координатный столбец предыдущего присоединенного вектора.

Пример. Найдем базис из собственных и присоединенных векторов линейного оператора , матрица которого в некотором базисе совпадает с матрицей

▼ Находим собственные значения.

.

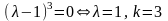Таким образом, имеем единственное собственное значение, кратность которого равна 3. Определим количество собственных и присоединенных векторов.

,

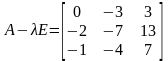, значит, в искомом базисе – один собственный вектор и два присоединенных. Находим собственный вектор, решая однородную систему с матрицей .

4

7

. (4.59)

Получаем систему:

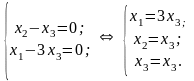
В качестве собственного вектора можно взять, например, частное решение 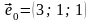. Теперь находим первый присоединенный вектор, дописывая в цепочке (4.59) к матрице в качестве столбца свободных членов координатный столбец найденного собственного вектора и пересчитывая столбец свободных членов по намеченным стрелкам:

.

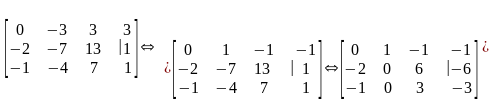
Получаем систему

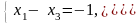(4.60)

Первый присоединенный вектор находим как частное решение системы (4.60): , а второй – как решение системы с той же матрицей, но в качестве столбца свободных членов уже дописываем координатный столбец вектора 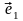, и опять пересчитываем его по намеченным стрелкам:

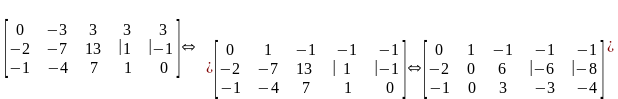
(4.61)

Частное решение системы (4.61) и будет вторым присоединенным вектором: .

Итак, искомый базис: 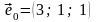– собственный; – 1-й присоединенный; – 2-й присоединенный векторы. ▲

Замечание. На практике все три цепочки объединяются в одну, новый столбец свободных членов дописывается к матрице предыдущей системы и пересчитывается по намеченным стрелкам.