
- •Коллоквиум по ла
- •Определение линейного пространства и простейшие следствия из аксиом
- •Примеры линейных пространств
- •Простейшие следствия из аксиом.
- •Вопрос 2 Линейная зависимость и независимость элементов линейного пространства
- •Примеры линейной зависимости и независимости
- •Простейшие свойства линейной зависимости
- •Вопрос 3 Базис и координаты в линейном пространстве
- •Примеры
- •Свойства координат векторов
- •Вопрос 4 Матричный критерий линейной зависимости и независимости
- •Вопрос 5 Размерность линейного пространства
- •Простейшие следствия из аксиом
- •Вопрос 7
- •Свойства скалярного произведения
- •Свойства расстояния
- •Вопрос 8 Подпространства линейного пространства
- •Вопрос 9 Линейные оболочки
- •Вопрос 10
- •Вопрос 11
- •Сумма и пересечение подпространств линейного пространства
- •Вопрос 12
- •Вопрос 13
- •Вопрос 14
- •Вопрос 15
- •Понятие отображения
- •Вопрос 16
- •Примеры линейных операторов
- •Простейшие свойства линейного оператора
- •Вопрос 17
- •Примеры
- •Связь координат вектора с координатами его образа
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Свойства изоморфизма
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Свойства собственных векторов
- •Вопрос 28
- •Правило нахождения собственных векторов
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32
- •Правило нахождения присоединенных векторов
- •Таким образом, имеем единственное собственное значение, кратность которого равна 3. Определим количество собственных и присоединенных векторов.
Связь координат вектора с координатами его образа
Пусть в линейном
пространстве
задан базис (4.8) и пусть
– матрица линейного оператора
в этом базисе. Выберем произвольный
вектор
и положим
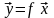 .
Обозначим
и
.
Обозначим
и
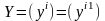 – координатные столбцы векторов
и
соответственно в базисе (4.8). Тогда
– координатные столбцы векторов
и
соответственно в базисе (4.8). Тогда
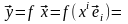 [(4.3)]
[(4.3)]
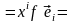 [(4.11)]
=
[(4.11)]
=
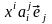 ,
,
и
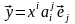 .
(4.13)
.
(4.13)
Равенство (4.13) есть не что иное, как разложение вектора по базису (4.8), а коэффициенты разложения –координаты вектора в этом базисе. В силу единственности координат вектора в данном базисе получаем
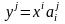 .
(4.14)
.
(4.14)
Записав
(4.14) по правилу цепочки (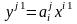 ),
получаем
),
получаем
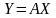 .
(4.15)
.
(4.15)
Формула (4.14) и задает связь координат вектора и координат его образа при линейном операторе, а (4.15) –ее матричная запись.
Вопрос 18
Изменение матрицы линейного оператора при изменении базиса. Подобные матрицы.
Теорема 4.2. Пусть в линейном пространстве заданы два базиса:
(4.16)
и
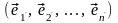 ,
(4.17)
,
(4.17)
и
пусть A =
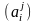 и
и
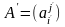 – матрицы линейного оператора
в базисах (4.16) и (4.17) соответственно.
Тогда
– матрицы линейного оператора
в базисах (4.16) и (4.17) соответственно.
Тогда
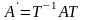 ,
(4.18)
,
(4.18)
где Т – матрица перехода от (4.16) к (4.17).
►Чтобы найти
матрицу
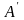 ,
следует образы векторов базиса (4.17)
разложить опять же по этому базису.
Имеем
,
следует образы векторов базиса (4.17)
разложить опять же по этому базису.
Имеем
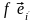 =
[определение матрицы перехода] =
=
[определение матрицы перехода] =
 = [(4.3)] =
= [(4.3)] =
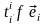 =
=
=
[(4.11)] =
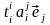 = [свойство 6º § 9 гл. 3] =
= [свойство 6º § 9 гл. 3] =
 .
.
Итак,
= . (4.19)
Равенство (4.19) задает разложение вектора по базису (4.17). С другой стороны, по определению матрицы линейного оператора,
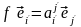 .
(4.20)
.
(4.20)
В силу единственности координат вектора в данном базисе из (4.19) и (4.20) получаем равенство
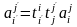 ,
(4.21)
,
(4.21)
которое и дает нам связь элементов матриц линейного оператора в различных базисах. Запишем (4.21) по правилу цепочки:
 .
(4.22)
.
(4.22)
Так
как
 (см. замечание в § 9 гл. 3), то из (4.22) получаем
(4.18).◄
(см. замечание в § 9 гл. 3), то из (4.22) получаем
(4.18).◄
Определение.
Квадратные матрицы А
и В
называются подобными,
если существует невырожденная матрица
Т
такая, что
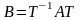 .
.
Таким образом, мы видим, что матрицы линейного оператора в различных базисах подобны.
Лемма 4.1.
Подобные матрицы имеют одинаковые
определители. ► .◄
.◄
Определение. Определителем линейного оператора называется определитель его матрицы в некотором, а значит, и в любом базисе пространства .
