Простейшие следствия из аксиом.
Линейное пространство впредь будем обозначать буквой V.
1º. В линейном пространстве существует единственный нейтральный элемент.
►
Предположим, что
в некотором линейном пространстве
есть два нейтральных элемента:
и
.
Тогда
Итак, мы пришли к противоречию.◄
2º. В линейном пространстве, каждый элемент имеет единственный противоположный.
►Предположим,
что некоторый элемент
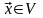имеет два различных противоположных:
и
,
т. е.
.
Получаем
–
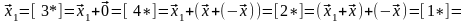
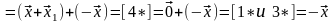опять пришли к противоречию.◄
3º.
►
◄
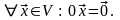
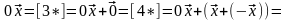
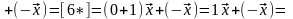
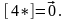Замечание. При доказательстве следствий можно использовать либо аксиомы, либо уже доказанные следствия.
4º.
►
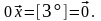
Таким
образом,
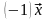– противоположный к
.
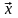Поэтому на основании 2-го следствия
◄
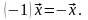5º.
►
◄
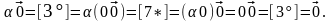6º.
В линейном пространстве из равенства
вытекает: либо
,
либо
.
►а) – утверждение верно.
б)
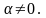Тогда имеем:
◄
Вопрос 2 Линейная зависимость и независимость элементов линейного пространства
Определение. Система элементов
(3.1)
линейного
пространства
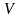над полем Р называется линейно
зависимой, если существуют числа
из поля Р, не все равные 0, такие
что
.
(3.2)
Система (3.1) называется линейно независимой, если равенство (3.2) выполняется только в том случае, когда
,
(3.3)
т. е. когда из равенства (3.2) вытекает (3.3).
Примеры линейной зависимости и независимости
1.
V = C,
P = C;
.
Положим
.
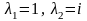Очевидно,
,
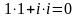значит, 1 и i линейно
зависимы над полем С.
2.
V = C,
P = R;
.
В этом случае в качестве
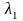и
комплексные числа использовать нельзя.
Составим равенство (3.2):
,
.
(3.4)
В
равенстве (3.4) числа
и
–
соответственно действительная и мнимая
части комплексного числа, которое равно
0, поэтому равны 0 и его действительная
и мнимая части, т. е.
.
Таким образом, числа 1 и i
над полем действительных чисел линейно
независимы.
3.
Так как
то
существуют числа
,
среди которых есть отличные от нуля,
такие что равенство (3.2) выполняется, и
рассматриваемые функции линейно
зависимы.
4. В следующих двух примерах приводятся два основных метода доказательства линейной независимости функций.
а) Метод частных
значений.
.
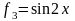Составляем равенство
(3.2):
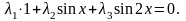(3.5)
Заметим, что в
правой части равенства (3.2) – нейтральный
элемент линейного пространства, значит,
в правой части (3.5) – нейтральный элемент
пространства функций, т. е. функция,
тождественно равная 0. Равенство (3.5)
следует понимать как равенство функций,
оно справедливо для всех
.
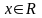Например, получаем:
Таким образом, рассматриваемая система функций линейно независима.
б) Используем
производные.
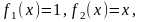
Составляем равенство (3.2):
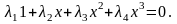(3.6)
Равенство (3.6) справедливо опять же для любого , т. е. функция
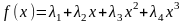
тождественно
равна 0, значит, тождественно равна 0 и
любая ее производная. Имеем:
При
получаем:
=
0, следовательно, рассматриваемая система
функций линейно независима.
5.
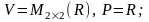
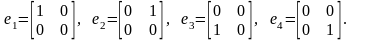(3.7)
Составляем линейную комбинацию и приравниваем ее нейтральному элементу:
следовательно, система (3.7) линейно независима.
6.
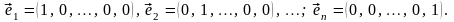(3.8)
Как обычно, составляем линейную комбинацию и приравниваем ее нейтральному элементу:
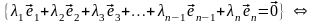
и поэтому, система (3.7) линейно независима.
Упражнение.
Докажите, что для любого натурального
система функций
линейно независима.