Вопрос 10

Теорема о размерности линейной оболочки строк (столбцов) матрицы

Теорема 3.6. Размерность линейной оболочки строк (столбцов) матрицы А равна ее рангу.

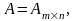
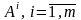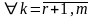
Доказательство проведем для строк матрицы. Пусть , и пусть базисный минор матрицы А расположен в первых r ее строках. Обозначим, как и раньше, – строки матрицы А. Тогда по теореме о базисном миноре система линейно независима, и 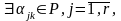такие, что 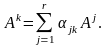Дальше точно так же, как и при доказательстве теоремы 3.5, показываем, что - система образующих в , а значит, и базис, и поэтому . Для столбцов доказательство проводится аналогично. 

Следствие. Ранг матрицы совпадает с максимальным числом линейно независимых ее строк (столбцов).

Пусть 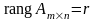, а максимальное число линейно независимых строк матрицы равно k. Тогда

k = [теорема 3.5] = 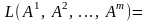[теорема 3.6] = r. 

Вопрос 11

Сумма и пересечение подпространств линейного пространства. Теорема о сумме и пересечении подпространств.

Сумма и пересечение подпространств линейного пространства

Определения. Пересечением подпространств и линейного пространства V над P называется его подмножество

Суммой подпространств и называется подмножество

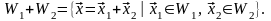
Сумма подпространств называется прямой и обозначается если .

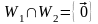Теорема 3.7. Сумма и пересечение подпространств линейного пространства также являются его подпространствами.

►Пусть и – подпространства линейного пространства V над P. Тогда

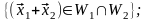
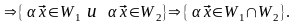
Таким образом, выполняются условия теоремы 3.4, значит, – подпространство пространства V.

Докажем теперь, что сумма подпространств – подпространство. Действительно,

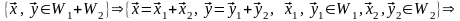
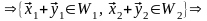
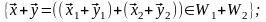
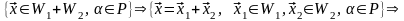
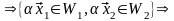
Итак, в этом случае условия теоремы 3.4 также выполняются, и поэтому, 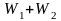– также подпространство пространства V. 

Вопрос 12

Теорема о размерности прямой суммы

Теорема 3.8. Размерность прямой суммы подпространств равна сумме их размерностей.

►Пусть и – подпространства линейного пространства V над P, , 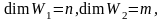и пусть

– (3.38)

базис , а

– (3.39)

базис . Покажем, что

– (3.40)

базис .

Действительно, 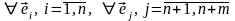: 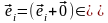, 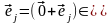.Кроме того,

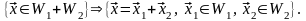
Тогда 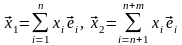, значит, ,

и, таким образом, (3.40) – система образующих в .

Линейную независимость (3.40) докажем на основании определения.

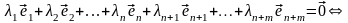
. (3.41)

Вектор в левой части (3.41) принадлежит пространству , а в правой – пространству . Так как сумма прямая, то , поэтому

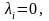
На основании линейной независимости (3.38) и (3.39), получаем , откуда и вытекает линейная независимость (3.40). Таким образом, (3.40) – линейно независимая система образующих пространства , а значит, и его базис, и поэтому

.
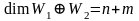