Вопрос 22

Обратный линейный оператор

Теорема 4.7. Для любого невырожденного линейного оператора существует единственный обратный оператор 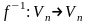, который также является линейным. При этом, если А – матрица оператора в некотором базисе, то матрица оператора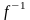 в том же базисе совпадает с матрицей .

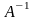►Единственность. Пусть некоторый оператор имеет два разных обратных: и 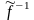. Тогда

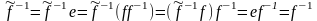
– противоречие.

Существование. Пусть А – матрица оператора в некотором базисе. Тогда, по теореме 4.4 , значит, существует . Обозначим – тот линейный оператор, матрица которого в выбранном базисе совпадает с .

Так как , и так как произведению матриц соответствует произведение операторов, то 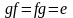, и, таким образом, .◄

Замечание. Можно доказать, что любой взаимно однозначный линейный оператор имеет единственный обратный, который тоже является линейным.

Вопрос 23

Определение и свойства изоморфизма линейных пространств

Определение. Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм , то линейные пространства и называются изоморфными. Изоморфизм обозначается так: .

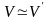Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства . Поэтому в математике изоморфные объекты не различаются.

Свойства изоморфизма

1. – рефлективность (изоморфизм осуществляет тождественное отображение).

2. – симметричность (если первый изоморфизм осуществляет с помощью отображения f, то второй – с помощью ).

3. { , 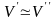} 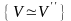– транзитивность (если первый изоморфизм осуществляется с помощью отображения , второй – , то третий изоморфизм осуществляется с помощью отображения ).

Строгого доказательства этих свойств мы не приводим.

Вопрос 24

Определение изоморфизма линейных пространств. Теорема о размерности изоморфных пространств

Определение. Изоморфизмом линейных пространств называется взаимно однозначный линейный оператор. Если существует изоморфизм , то линейные пространства и называются изоморфными. Изоморфизм обозначается так: .

Так как изоморфизм – взаимно однозначное отображение, то изоморфные объекты содержат одинаковое количество элементов. Кроме того, в силу линейности, действия, производимые над элементами пространства , одновременно производятся и над элементами пространства . Поэтому в математике изоморфные объекты не различаются.

Теорема 4.8. Изоморфные линейные пространства имеют одинаковые размерности.

►Пусть 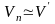и пусть – изоморфизм. Выберем в какой-либо базис

(4.27)

и покажем, что система

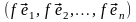– (4.28)

базис пространства . Действительно, в силу взаимной однозначности f, 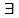единственный такой, что . Тогда, если , то 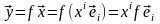. Значит, (4.28) – система образующих в .

Докажем теперь линейную независимость (4.28).

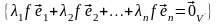[линейность f]

[взаимная однозначность f ] [линейная независимость (4.27)] 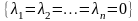{(4.28) – линейно независима}.

Таким образом, (4.28) – базис в , а значит, . ◄