Вопрос 4 Матричный критерий линейной зависимости и независимости

Пусть в линейном пространстве V задан некоторый базис, тогда каждый вектор можно разложить по этому базису.

Координатным столбцом вектора 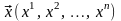в заданном базисе будем называть столбец 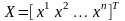, составленный из координат вектора в этом базисе.

Лемма 3.1. Для того чтобы векторы были линейно зависимыми, необходимо и достаточно, чтобы их координатные столбцы в некотором базисе были линейно зависимыми.

► Пусть заданы векторы

, (3.26)

– их координатные столбцы в некотором базисе. Одновременно проводим доказательство и необходимости, и достаточности. Согласно следствию из свойств координат векторов, координатный столбец линейной комбинации векторов равен такой же линейной комбинации координатных столбцов векторов-слагаемых. Имеем:

{(3.26) линейно зависима}

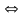
, не все равные нулю, что

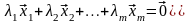
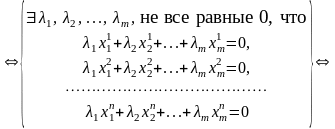
, не все равные нулю, что {столбцы линейно зависимы}.◄

Теорема 3.1 (матричный критерий). Для того чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы ранг матрицы, составленной из координатных столбцов этих векторов в некотором базисе, был меньше количества векторов.

Для того чтобы система векторов была линейно независимой, необходимо и достаточно, чтобы ранг матрицы, составленной из координатных столбцов этих векторов, был равен их количеству.

Доказательство вытекает из леммы 3.1 и теоремы 2.4.

Вопрос 5 Размерность линейного пространства

Определение. Число n называется размерностью линейного пространства V, а само пространство V называется n-мерным, если в V существует линейно независимая система из n векторов, а любая система из (n + 1)-го вектора линейно зависима. Размерность пространства 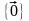по определению считается равной нулю.

Следствие. В n-мерном пространстве любая система из m векторов при m > n линейно зависима.

Размерность линейного пространства V сокращенно обозначается 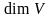. Если , то пространство будем обозначать 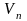. Линейные n-мерные пространства называются конечномерными.

Определение. Линейное пространство V называется бесконечномерным, если 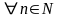в V найдется линейно независимая система из n векторов.

Теорема 3.2. Для того чтобы линейное пространство было n-мерным, необходимо и достаточно, чтобы в нем существовал базис, состоящий из n векторов.

► Достаточность. Дано: в пространстве V существует базис из n векторов

( ). (3.27)

Тогда в V есть линейно независимая система из n векторов (это система (3.27)). Покажем, что любая система из (n + 1)-го вектора в этом пространстве линейно зависима. Выберем одну из них:

( ). (3.28)

Каждый вектор системы (3.28) можно разложить по базису (3.27). Обозначим 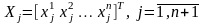– координатные столбцы векторов системы (2) в базисе (1). Тогда

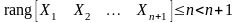
(так как эта матрица имеет только n строк). По матричному критерию система (3.28) линейно зависима и, таким образом, .

Необходимость. Дано: . Согласно определению, в пространстве 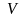существует линейно независимая система из элементов. Пусть

( ) – (3.29)

одна из таких систем. Но 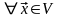система

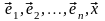( ) (3.30)

линейно зависима. По 4-му свойству линейной зависимости (§ 2) вектор

можно представить в виде линейной комбинации векторов системы (3.29), т. е.

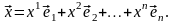
Таким образом, (3.29) – система образующих пространства V, а значит, и его базис. ◄

Замечание. При доказательстве необходимости мы одновременно показали, что в n-мерном пространстве любая линейно независимая система из n векторов является базисом.

Следствие. Любой базис конечномерного линейного пространства V содержит одинаковое количество векторов.

►Пусть в пространстве наряду с базисом (3.29) есть еще и некоторый базис

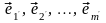( ), (3.31)

состоящий из m векторов (m ≠ n). Рассмотрим два случая:

а) m > n. Тогда (3.31) линейно зависима согласно следствию к определению размерности, что противоречит определению базиса.

б) m < n. Так как (3.31) – базис пространства , то по теореме 3.2 , поэтому система (3.29) линейно зависима, что противоречит определению базиса. Таким образом, m = n. ◄

Вывод: размерность линейного пространства совпадает с количеством векторов в любом из его базисов.

Используя примеры базисов, приведенные в § 3, можно утверждать, что: 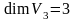, , 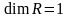, , 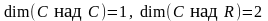, 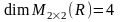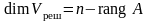. Примером бесконечномерного пространства может служить пространство всех функций.

Упражнение. Докажите, что .

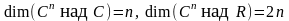Теорема 3.3. В n-мерном линейном пространстве любую линейно независимую систему из m векторов при m < n можно дополнить до базиса.

►Пусть

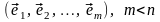– (3.32)

линейно независимая система пространства . Предположим, что при всех 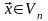система линейно зависима. Тогда на основании свойства 4º § 2, вектор можно выразить через векторы системы (3.32), поэтому (3.32) – система образующих, а значит, и базис пространства , следовательно, 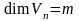, что противоречит условию. Таким образом, найдется вектор 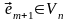такой, что система

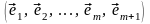– (3.33)

линейно независима. Если m + 1 = n, то (3.33) – базис пространства . В противном случае с системой (3.33) поступаем так же, как и с системой (3.32). После конечного числа шагов получаем базис пространства .◄

В

опрос 6

Определение аффинного пространства и следствия из аксиом

Определение. Пусть А – множество элементов произвольной природы, V – действительное линейное пространство. А называется аффинным пространством, связанным с линейным пространством V, если задан закон, по которому каждой паре элементов 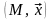, где 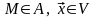, ставится в соответствие элемент 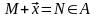, причем выполняются две аксиомы.

1*.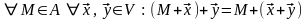 (рис. 3.1).

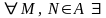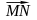2*. единственный такой, что . Этот вектор обозначается . Таким образом, 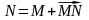(рис. 3.2).

Элементы аффинного пространства называются точками, а операция в аффинном пространстве называется откладыванием вектора от точки.

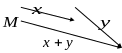
Рис. 3.1 Рис. 3.2

Как видим, аксиомы аффинного пространства просто «списаны» со школьного точечного трехмерного пространства.