- •Коллоквиум по ла
- •Определение линейного пространства и простейшие следствия из аксиом
- •Примеры линейных пространств
- •Простейшие следствия из аксиом.
- •Вопрос 2 Линейная зависимость и независимость элементов линейного пространства
- •Примеры линейной зависимости и независимости
- •Простейшие свойства линейной зависимости
- •Вопрос 3 Базис и координаты в линейном пространстве
- •Примеры
- •Свойства координат векторов
- •Вопрос 4 Матричный критерий линейной зависимости и независимости
- •Вопрос 5 Размерность линейного пространства
- •Простейшие следствия из аксиом
- •Вопрос 7
- •Свойства скалярного произведения
- •Свойства расстояния
- •Вопрос 8 Подпространства линейного пространства
- •Вопрос 9 Линейные оболочки
- •Вопрос 10
- •Вопрос 11
- •Сумма и пересечение подпространств линейного пространства
- •Вопрос 12
- •Вопрос 13
- •Вопрос 14
- •Вопрос 15
- •Понятие отображения
- •Вопрос 16
- •Примеры линейных операторов
- •Простейшие свойства линейного оператора
- •Вопрос 17
- •Примеры
- •Связь координат вектора с координатами его образа
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Свойства изоморфизма
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Свойства собственных векторов
- •Вопрос 28
- •Правило нахождения собственных векторов
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •Вопрос 32
- •Правило нахождения присоединенных векторов
- •Таким образом, имеем единственное собственное значение, кратность которого равна 3. Определим количество собственных и присоединенных векторов.
Вопрос 3 Базис и координаты в линейном пространстве
Определение. Базисом линейного пространства V над полем Р называется упорядоченная система
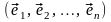 (3.18)
(3.18)
элементов этого пространства, удовлетворяющая следующим условиям:
1)
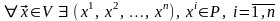 ,
такие, что
,
такие, что
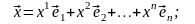 (3.19)
(3.19)
2) система (3.18) линейно независима.
Если система (3.18) удовлетворяет только одному первому условию, то она называется системой образующих линейного пространства V. Таким образом, базис линейного пространства – это его линейно независимая система образующих.
Числа
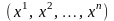 в равенстве (3.19) называются координатами
вектора
в базисе (3.18), а само равенство (3.19) –
разложением вектора
по базису (3.18). Таким образом, координаты
вектора в данном базисе – это коэффициенты
в разложении этого вектора по базису.
в равенстве (3.19) называются координатами
вектора
в базисе (3.18), а само равенство (3.19) –
разложением вектора
по базису (3.18). Таким образом, координаты
вектора в данном базисе – это коэффициенты
в разложении этого вектора по базису.
Примеры
1. Вспомним, что в пространстве свободных векторов мы назвали базисом любую упорядоченную тройку некомпланарных (т. е. линейно независимых) векторов и показали, что всякий вектор можно по этому базису разложить. Таким образом, мы видим, что понятие базиса в произвольном линейном пространстве – это обобщение понятия базиса в пространстве свободных векторов.
2.
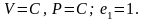 Так как
Так как
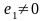 ,
то (
,
то (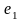 )
– линейно
независима. Кроме того,
)
– линейно
независима. Кроме того,
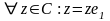 ,
а значит, система (
)
является и системой образующих и поэтому
базисом.
,
а значит, система (
)
является и системой образующих и поэтому
базисом.
3.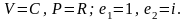
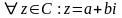
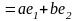 .
Таким образом, (1, i)
– система образующих в C
над R,
линейная независимость которой доказана
в § 2. Следовательно – это и базис.
.
Таким образом, (1, i)
– система образующих в C
над R,
линейная независимость которой доказана
в § 2. Следовательно – это и базис.
4.
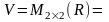
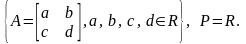
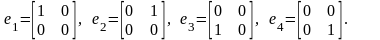 (3.20)
(3.20)
Тогда
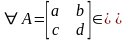
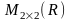
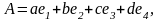
следовательно, (3.20) – система образующих пространства . В § 2 доказано, что эта система линейно независима, значит, она является и базисом линейного пространства .
5. Базисом в
пространстве
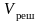 является фундаментальная система
решений.
является фундаментальная система
решений.
6.
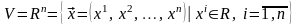 ,
,
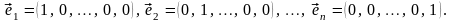 (3.21)
(3.21)
Очевидно,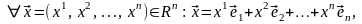 поэтому (3.21) – система образующих
пространства
поэтому (3.21) – система образующих
пространства
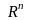 .
Так как эта система ещё и линейно
независима (см.
§ 2), то она является базисом пространства
.
Этот базис впредь будем называть
каноническим.
.
Так как эта система ещё и линейно
независима (см.
§ 2), то она является базисом пространства
.
Этот базис впредь будем называть
каноническим.
Свойства координат векторов
1º. Если все координаты вектора в некотором базисе равны нулю, то этот вектор – нулевой.
►Доказательство
очевидным образом вытекает из аксиом
линейного пространства и следствий
к ним:
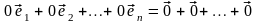 .
◄
.
◄
2º. Все координаты нулевого вектора в любом из базисов равны нулю.
►Пусть
(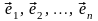 )
–
(3.22) базис линейного пространства
;
)
–
(3.22) базис линейного пространства
;
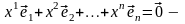 (3.23)
(3.23)
разложение нулевого
вектора по базису (3.22). В
силу линейной независимости (3.22)
из (3.23) вытекает, что
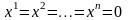 .
◄
.
◄
3º. Координаты вектора в данном базисе определяются однозначно.
►Пусть
некоторый вектор
в базисе (3.22) имеет два разных набора
координат:
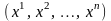 и
и
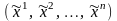 .
Тогда
.
Тогда
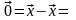
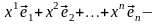 (
(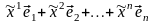 )
=
)
=
= [аксиомы 1*, 2* и 6* из определения линейного пространства] =
=
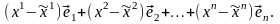 (3.24)
(3.24)
Равенство (3.24) – это
разложение по базису (3.22) нулевого
вектора, и поэтому все коэффициенты
разложения равны нулю, следовательно,
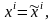
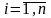 ,
что противоречит условию. ◄
,
что противоречит условию. ◄
4º. При сложении векторов их соответствующие координаты складываются.
►
Пусть заданы векторы
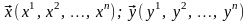 своими координатами в базисе (3.22) и пусть
своими координатами в базисе (3.22) и пусть
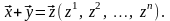 Тогда
Тогда
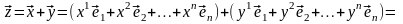
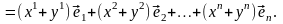 (3.25)
(3.25)
Равенство
(3.25) – это разложение вектора
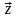 по базису (3.22), следовательно, коэффициенты
разложения – координаты вектора
в базисе (3.22). В силу единственности
координат вектора в данном базисе
получаем:
по базису (3.22), следовательно, коэффициенты
разложения – координаты вектора
в базисе (3.22). В силу единственности
координат вектора в данном базисе
получаем:
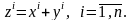 ◄
◄
5º. При умножении вектора на число все его координаты умножаются на это число.
Свойство доказывается точно так же, как и предыдущее, это вы можете сделать самостоятельно.
Следствие.
Координаты линейной комбинации векторов
равны таким же (с такими же коэффициентами)
линейным комбинациям соответствующих
координат слагаемых, т. е. если
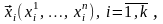 и
и
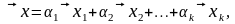
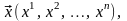 то
то