Простейшие свойства линейной зависимости
1º. Система, содержащая нейтральный элемент, линейно зависима.
►Пусть система
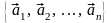(3.9)
содержит
нейтральный элемент и пусть,
например,
.
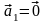Положим
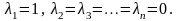(3.10)
Среди чисел (3.10) есть отличные от нуля и
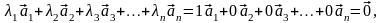
значит, система (3.9) линейно зависима. ◄
2º. Система, содержащая линейно зависимую подсистему, линейно зависима.
►Пусть система
(3.9) содержит линейно зависимую подсистему
и пусть, например, подсистема
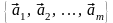при
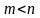линейно
зависима. Это означает, что существуют
числа
,
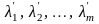(3.11) не все равные
0, такие что
.
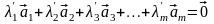Положим
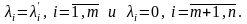(3.12)
Среди чисел (3.12) есть отличные от 0, так как таковые есть среди чисел (3.11), и
.
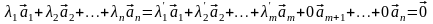Таким образом, исходная система линейно зависима. ◄
Следствие. Любая подсистема линейно независимой системы линейно независима.
3º. Критерий линейной зависимости. Для того чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы один из векторов можно было представить в виде линейной комбинации остальных.
►Необходимость.
Дано: система
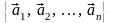линейно
зависима. Значит, существуют числа
,
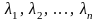не все равные 0, такие, что справедливо
равенство
. (3.13)
Пусть,
например,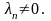
Тогда из (3.13) можно выразить
:
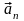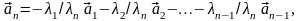
что и требовалось доказать.
Достаточность.
Дано: один из векторов можно представить
в виде линейной комбинации остальных,
например,
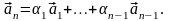Положим
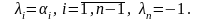(3.14)
Cреди
чисел (3.14) есть отличные от 0 и
,
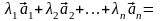
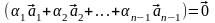значит, исходная
система линейно зависима. ◄
4º. Пусть система
(3.15)
линейно независима, а система
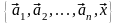– (3.16)
линейно зависима. Тогда можно представить в виде линейной комбинации элементов системы (3.15).
►В силу линейной
зависимости системы (3.16) существуют
числа
не все равные 0, такие, что
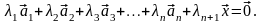(3.17)
Предположим,
что
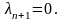Значит, среди чисел
есть отличные от нуля, и из (3.17) вытекает,
что
что противоречит линейной независимости
(3.15). Таким образом,
,
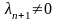и из (3.17) получаем требуемое утверждение.◄
5º. Для того чтобы система из одного элемента была линейно зависимой, необходимо и достаточно, чтобы он был нулевым.
►Достаточность вытекает из первого свойства.
Необходимость.
Пусть система
линейно зависима, тогда существует
число
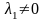такое, что
.
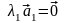Значит, на основании 6-го следствия из
аксиом (§1)
.◄
Следующие свойства формулируем для пространства свободных векторов.
6º. Для того чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными.
7º. Для того чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были компланарными.
►Доказательство последних двух свойств вытекает из третьего свойства и критериев коллинеарности и компланарности из аналитической геометрии. ◄