Вопрос 28

Характеристический многочлен и характеристические числа линейного оператора и его матрицы. Правило нахождения собственных векторов. Лемма о решении вырожденной однородной системы линейных уравнений.

Правило нахождения собственных векторов

Пусть – линейный оператор. Выберем в какой-либо базис и обозначим А матрицу оператора в этом базисе. Если Х – координатный столбец собственного вектора в заданном базисе, а – соответствующее ему собственное значение, то (4.41) равносильно равенству 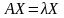, которое, в свою очередь, равносильно следующему:

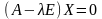. (4.47)

Равенство (4.47) можно рассматривать как матричную запись однородной системы линейных уравнений, причем нас интересуют только ее нетривиальные решения. Как следует из § 5 главы 2, для существования таковых необходимо и достаточно, чтобы выполнялось условие

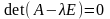. (4.48)

Определение. Характеристическим многочленом матрицы А называется многочлен 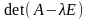, уравнение (4.48) называется характеристическим уравнением матрицы А, а корни этого уравнения – ее характеристическими числами.

Лемма 4.2. Подобные матрицы имеют одинаковые характеристические многочлены.

►Пусть матрицы А и подобны, значит, существует невырожденная матрица такая, что . Тогда

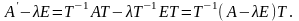
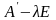Таким образом, матрицы и ( ) тоже подобны, а значит, имеют одинаковые определители.◄

Эта лемма позволяет сформулировать следующее

Определение. Характеристическим многочленом (характеристическим уравнением, характеристическими числами) линейного оператора называется характеристический многочлен (характеристическое уравнение, характеристические числа) его матрицы в некотором, а значит, и в любом базисе.

Из изложенного выше мы видим, что каждое собственное значение линейного оператора является корнем его характеристического уравнения, т. е. характеристическим числом. Обратно, если – корень уравнения (4.48) и 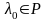, то система (4.47) имеет нетривиальное решение Х₀, значит, АХ₀ = Х₀ и тогда, если 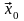– вектор, координатный столбец которого в выбранном базисе совпадает с 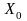, то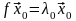 , т. е. – собственное значение оператора . Если же , то оно не может быть собственным значением согласно определению.

Итак, собственные значения линейного оператора – те его характеристические числа, которые принадлежат полю P.

Теперь можно сформулировать следующее правило. Пусть А – матрица линейного оператора в некотором базисе. Чтобы найти собственные векторы оператора поступаем следующим образом:

1) составляем характеристическое уравнение (4.48) матрицы А и находим его корни 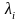. Те из них, которые принадлежат основному полю, являются собственными значениями (т. е., если Р = С, то все, если Р = R – только действительные);

2) для каждого из полученных собственных значений находим соответствующие ему собственные векторы, решая однородную систему (4.47) при .

Лемма 4.3. Если определитель однородной квадратной системы линейных уравнений

AX = О, (4.49)

равен нулю, то при любом набор

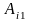( , , …, ), (4.50)

где – алгебраическое дополнение к элементу матрицы А, – решение системы (4.49).

►Действительно, подставив (4.50) в каждое из уравнений (4.49), получаем

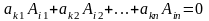. (4.51)

Равенство (4.51) верно, так как при 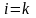его левая часть представляет собой разложение 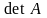по 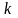-й строке, а при оно верно на основании теоремы аннулирования. ◄

Пример. Найдем собственные векторы линейного оператора 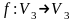, который в некотором базисе пространства V₃ имеет матрицу

.

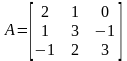▼ 1. Составляем характеристический многочлен:

.

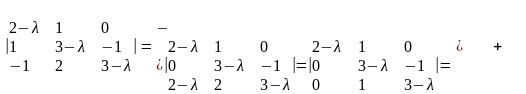
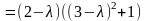Характеристическое уравнение оператора выглядит так:

,

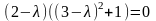а характеристическими числами будут λ₁ = 2; λ₂ = 3 – i; λ₃ = 3 + i. Если P = R, то собственное значение только одно – λ₁ = 2; если же P = C, то все значения будут собственными. Рассмотрим последний случай.

2. λ₁ = 2:

. (4.52)

Однородная система с матрицей (4.52) решается устно: . Значит, собственные векторы с этим собственным значением выглядят так: = α(1; 0; 1), .

λ₂=3 – i:

. (4.53)

Так как , то . Поэтому достаточно найти один собственный вектор, а все остальные будут ему коллинеарными. Для нахождения же этого вектора воспользуемся леммой 4.3 и найдем упорядоченный набор из алгебраических дополнений к элементам, например, первой строки матрицы (4.53): 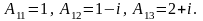Тогда все собственные векторы с собственным значением – это

.

λ₃=3 + i:

(4.54)

Заметим, что матрицы (4.53) и (4.54) – комплексно-сопряженные. Значит, и решения систем с этими матрицами – тоже комплексно-сопряженные, и поэтому ▲