Вопрос 16
Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора
Определение.
Пусть
и
–
линейные пространства над одним и тем
же полем
.
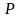Отображение
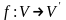называется линейным
оператором,
если оно удовлетворяет следующим
условиям:
1*.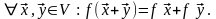
2*.
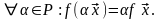
Следствие.
При линейном операторе образ линейной
комбинации векторов равен такой же
линейной комбинации их образов, т. е.
если
–
линейный оператор, то
:
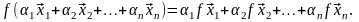(4.3)
Доказательство проведем методом математической индукции по количеству векторов.
а) n
= 1:
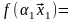[2*]
–
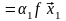истинно.
б) Предполагая, что утверждение верно для (n-1)-го вектора, доказываем его для n векторов.
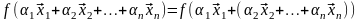= [1*] =
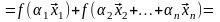[2*
и предположение индукции] =
=
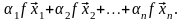
Примеры линейных операторов
1. Нулевой оператор
:
.
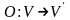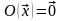Очевидно, этот оператор удовлетворяет
условиям 1* и 2*, значит, является линейным.
2. Тождественный
оператор
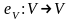также, очевидно, является линейным.
3. Оператор
дифференцирования
,
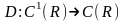который каждой дифференцируемой функции
ставит в соответствие ее производную,
является линейным, так как производная
суммы функций равна сумме их производных,
а при умножении функции на число ее
производная умножается на это число.
4. Пусть
– пространство свободных векторов,
Покажем,
что оператор проектирования на ось
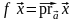является линейным.
►В аналитической
геометрии доказывалось, что
.
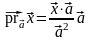Тогда
:
=
=
=
=
;
:
=
=
=
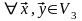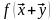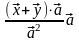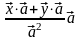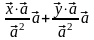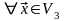
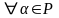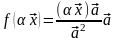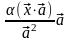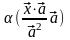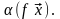
Таким образом, условия 1* и 2* выполняются, а значит, оператор проектирования вектора на ось является линейным.◄
5
.
В пространстве
векторов
плоскости, закрепленных в начале
координат О,
рассмотрим оператор
поворота вектора на угол
против часовой стрелки и докажем его
линейность.
►
Пусть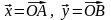
– произвольные векторы,
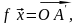
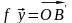(рис. 4.4),
.
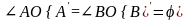Построим
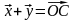и
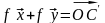по правилу параллелограмма. Так как
плоскость поворачивается
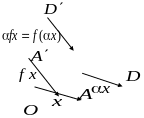Рис.4.4
как жесткое целое,
методами элементарной геометрии нетрудно
показать, что при этом повороте диагональ
переходит в диагональ
.
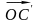Значит,
.
П
Рис. 4.5
усть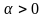
,
,
,
,
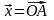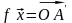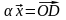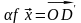(рис.4.5). Очевидно, вектор
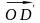получен из
поворотом на угол
,
следовательно,
,
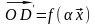а значит,
.
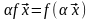Аналогично это свойство проверяется и
при
,
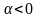а при
оно очевидно.◄
Теорема 4.1. Пусть и – линейные пространства над одним и тем же полем P и пусть в пространстве задан базис
,
(4.4)
а в пространстве – произвольная система векторов
.
(4.5)
Тогда
существует единственный линейный
оператор
,
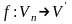переводящий базис (4.4) в систему (4.5), то
есть такой, что
:
.
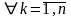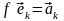(4.6)
►Построение. Выберем произвольный вектор и разложим его по базису (4.4): . Положим по определению
.
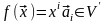Линейность.
Если
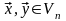– произвольные векторы,
,
то
,
,
,
.
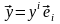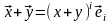
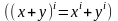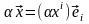Тогда
=
[определение f]
=
;
.
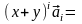
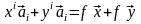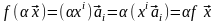Выполнение (4.6).
Заметим, что все координаты вектора
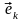в
базисе (4.3) равны нулю, за исключением
k-й,
которая равна 1. Таким образом, i-я
координата вектора
равна
,
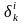то есть
.
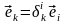Тогда
,
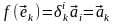значит, условие (4.6) выполнено.
Единственность.
Предположим, что существует еще один
линейный оператор
,
,
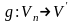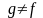переводящий (4.4) в (4.5), то есть такой, что
.
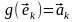Тогда
:
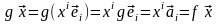– противоречие.◄