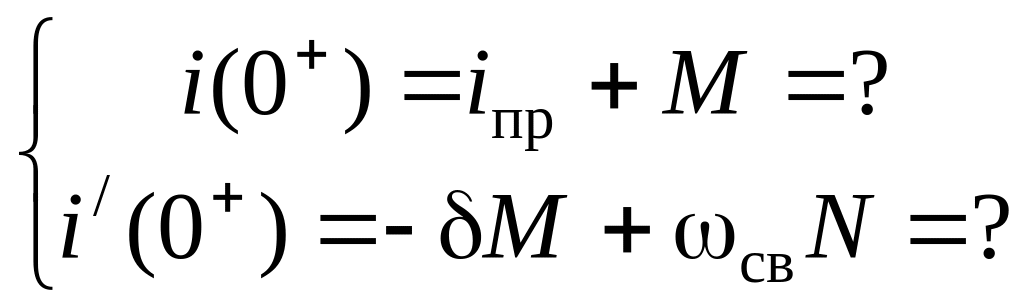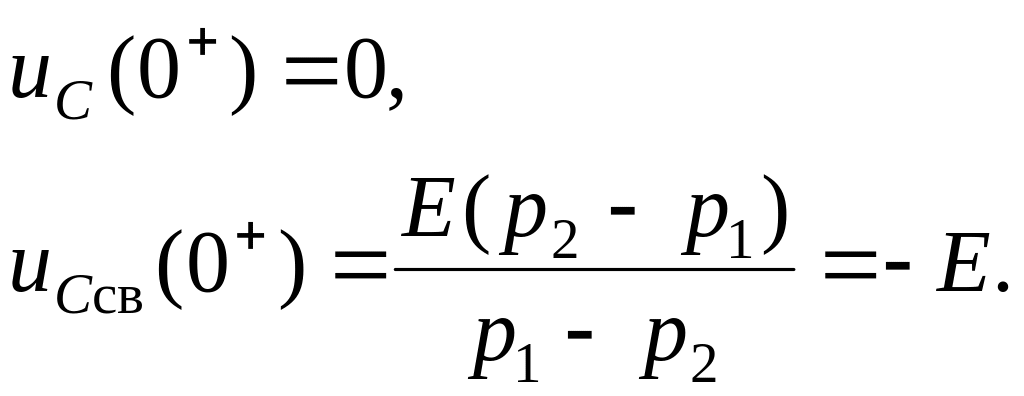- •Лекции по дисциплине «электротехника и электроника»
- •Глава 1 основные понятия и определения электрических цепей
- •Электрическая цепь и её элементы
- •Активные элементы
- •1.4 Пассивные элементы
- •1.5 Основные законы и уравнения электрических цепей
- •Глава 2. Основные свойства и методы расчета электрических цепей постоянного тока
- •2.1 Метод контурных токов
- •2.2 Принцип наложения и метод наложения
- •2.6 Метод узловых потенциалов
- •2.7 Метод эквивалентного генератора
- •2.8 Передача энергии от активного двухполюсника нагрузке
- •2.9 Преобразования в линейных электрических цепях
- •Глава 3 линейные цепи синусоидального тока
- •3.1 Синусоидальный ток и его основные характеристики
- •3.2 Получение синусоидальной эдс
- •3.3 Способы изображения синусоидальных величин
- •3.4 Законы Ома и Кирхгофа в комплексной форме
- •3.5 Пассивные элементы r, l, c в цепи синусоидального тока
- •3.6 Последовательное соединение элементов r, l, c в цепи синусоидального напряжения
- •3.7 Мгновенная и средняя мощности. Активная, реактивная и полная мощности. Измерение мощности ваттметром
- •3.8 Треугольники сопротивлений, напряжений и мощностей
- •3.9 Топографическая и векторная диаграммы
- •3.10 Резонанс напряжений
- •3.11 Резонанс токов
- •3.12 Частотные характеристики пассивных двухполюсников
- •3.13 Условие передачи максимальной мощности от активного двухполюсника нагрузке
- •3.14 Падение и потеря напряжения в линии передачи электроэнергии
- •Глава 4 цепи со взаимной индуктивностью
- •4.1 Индуктивно связанные элементы. Эдс взаимной индукции
- •Последовательное соединение индуктивно связанных элементов цепи
- •Параллельное соединение индуктивно связанных элементов цепи
- •4.4 Эквивалентная замена индуктивно связанных цепей
- •4 .5 Трансформатор. Вносимое сопротивление. Векторная диаграмма
- •Глава 5 расчёт трёхфазных электрических цепей
- •5.1. Основные понятия и определения
- •5.2 Основные схемы соединения трёхфазных цепей
- •5.3 Методы расчета трёхфазных цепей
- •5.3.1 Соединение звездой
- •5.3.2 Соединение треугольником
- •5.4 Измерение мощности в трёхфазных цепях
- •5.4 Аварийные режимы
- •5.5 Вращающееся магнитное поле
- •Глава 6 линейные цепи с несинусодальными источниками
- •6.1 Основные понятия и определения
- •6.2 Особенности расчета линейной электрической цепи с несинусоидальными источниками
- •6.3 Мощность при несинусоидальных источниках
- •6.4 Высшие гармоники в трёхфазных цепях
- •Глава 7 четырёхполюсники
- •7.1 Определение четырёхполюсника. Основные формы записи уравнений четырёхполюсника
- •7.2 Определение коэффициентов четырёхполюсника
- •7.2 Определение коэффициентов y, z, h, g и в форм уравнений через коэффициенты формы а
- •Эквивалентные схемы четырёхполюсника
- •7.4 Соединение четырехполюсников
- •8 Переходные процессы в линейных электрических цепях
- •8.1 Общие вопросы теории переходных процессов
- •4.2. Классический метод расчёта переходных процессов
- •4.2.1. Определение принужденной составляющей
- •4.2.2. Определение порядка цепи n
- •4.2.3. Определение корней характеристического уравнения
- •8.2.4. Определение постоянных интегрирования
- •8.2.5 Переходные процессы в цепях первого порядка
- •8.2.5.1 Разряд заряженной ёмкости через сопротивление r
- •8.2.5.2 Подключение r -цепи к источнику постоянного напряжения
- •4.2.5.3 Подключение rl-цепи к источнику постоянного напряжения
- •8.2.5.4 Подключение rc-цепи к источнику гармонического напряжения
- •8.2.6 Переходные процессы в цепях второго порядка
- •8.2.6.1 Разряд емкости на цепь rl
- •8.2.6.2 Апериодический разряд емкости на цепь rl
- •8.2.5.3 Колебательный заряд конденсатора
- •8.2.5.4 Общий случай расчета цепи второго порядка
- •8.3 Операторный метод расчета переходных процессов в линейных электрических цепях
- •8.3.1 Преобразование Лапласа. Основные теоремы операторного метода
- •Теоремы операторного метода
- •Ключевые теоремы
- •Некоторые типовые преобразования Лапласа
- •8.3.2 Законы Ома и Кирхгофа в операторной форме
- •8.3.3 Эквивалентные операторные схемы
- •8.3.4 Порядок расчета переходных процессов операторным методом
- •8.3.6 Расчет свободных составляющих операторным методом
8.2.6 Переходные процессы в цепях второго порядка
Одна из классических задач в теории переходных процессов – анализ разряда конденсатора на цепь RL.
8.2.6.1 Разряд емкости на цепь rl
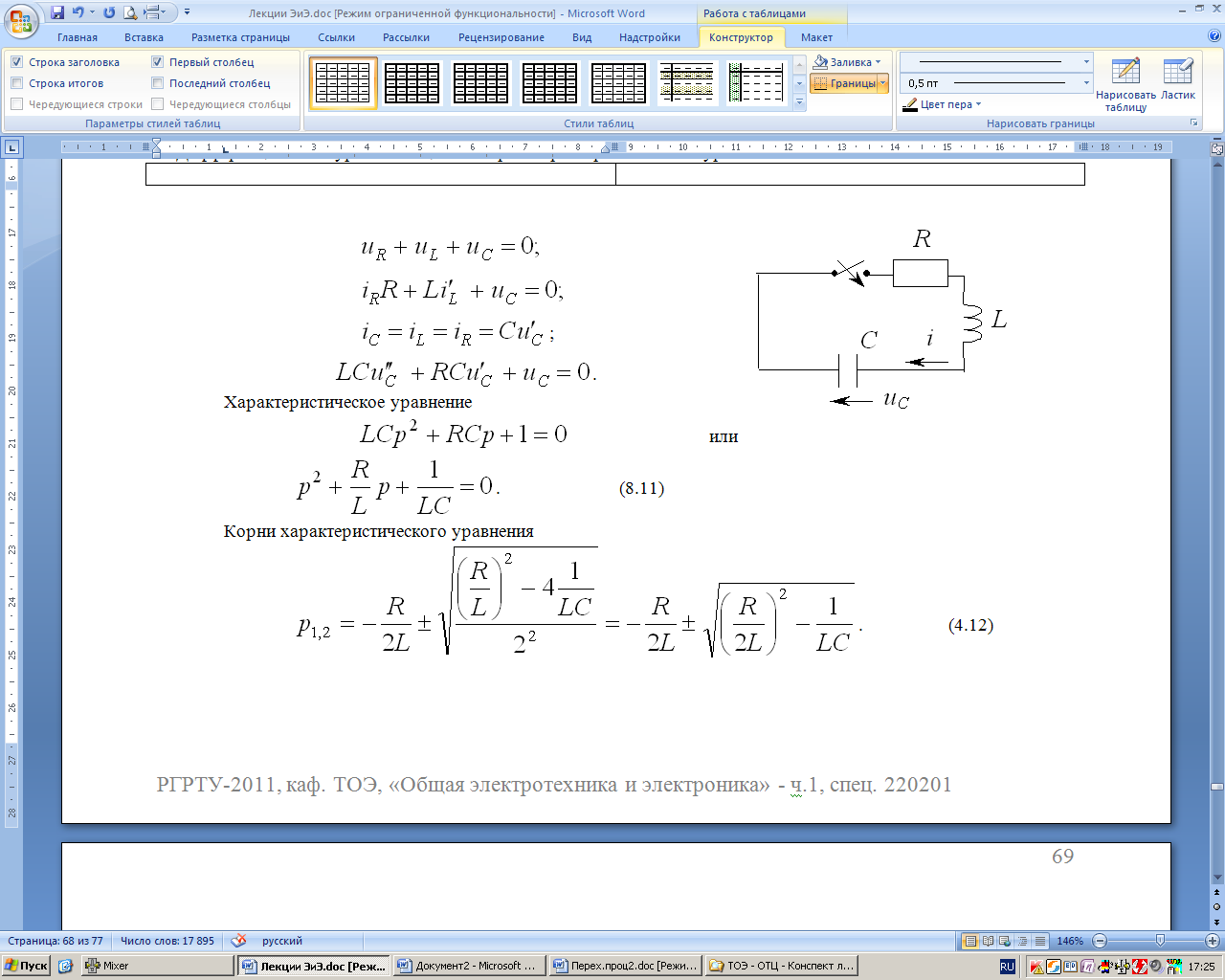
1. Независимые начальные условия для рассматриваемой цепи (рис. 8.15):
![]()
2. Дифференциальное уравнение цепи и корни характеристического уравнения:
Рис. 8.15 |
|
Характеристическое уравнение
![]() или
или
![]() . (8.11)
. (8.11)
Корни характеристического уравнения
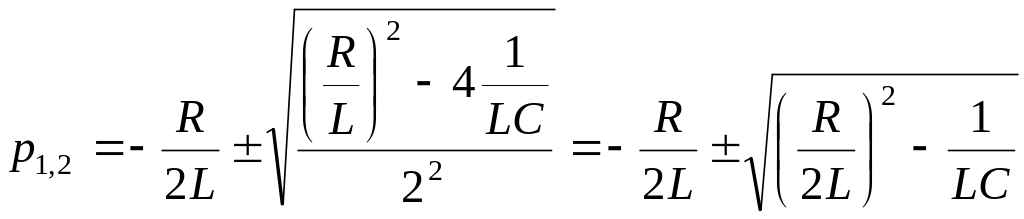 . (8.12)
. (8.12)
3. Полное
решение
![]() .
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (8.12). Здесь возможны
три варианта:
.
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (8.12). Здесь возможны
три варианта:
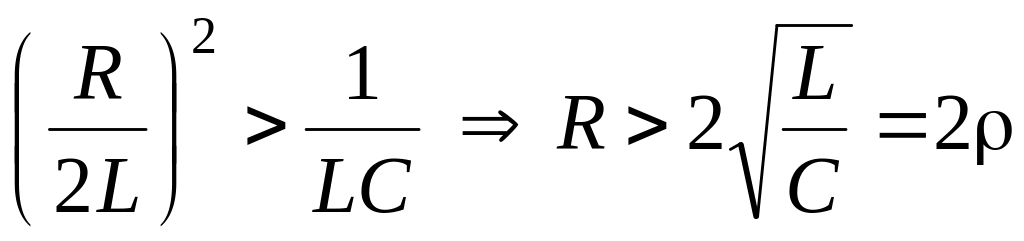 ,
где
– волновое сопротивление контура, т.е.
для низкодобротных контуров Q
< 0,5. При этом корни p1
и
p2
– вещественные
отрицательные разные.
,
где
– волновое сопротивление контура, т.е.
для низкодобротных контуров Q
< 0,5. При этом корни p1
и
p2
– вещественные
отрицательные разные.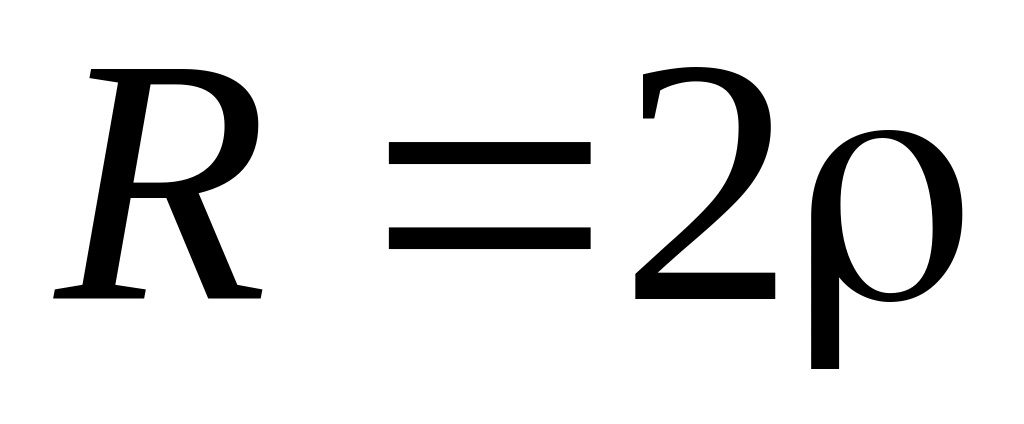 или
Q
= 0,5: корни p1
= p2
– вещественные отрицательные равные
или
Q
= 0,5: корни p1
= p2
– вещественные отрицательные равные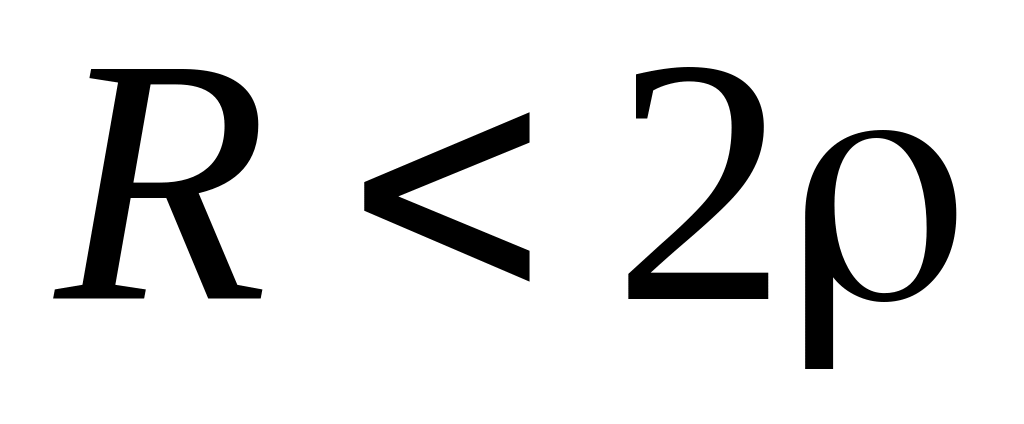 или
Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
или
Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
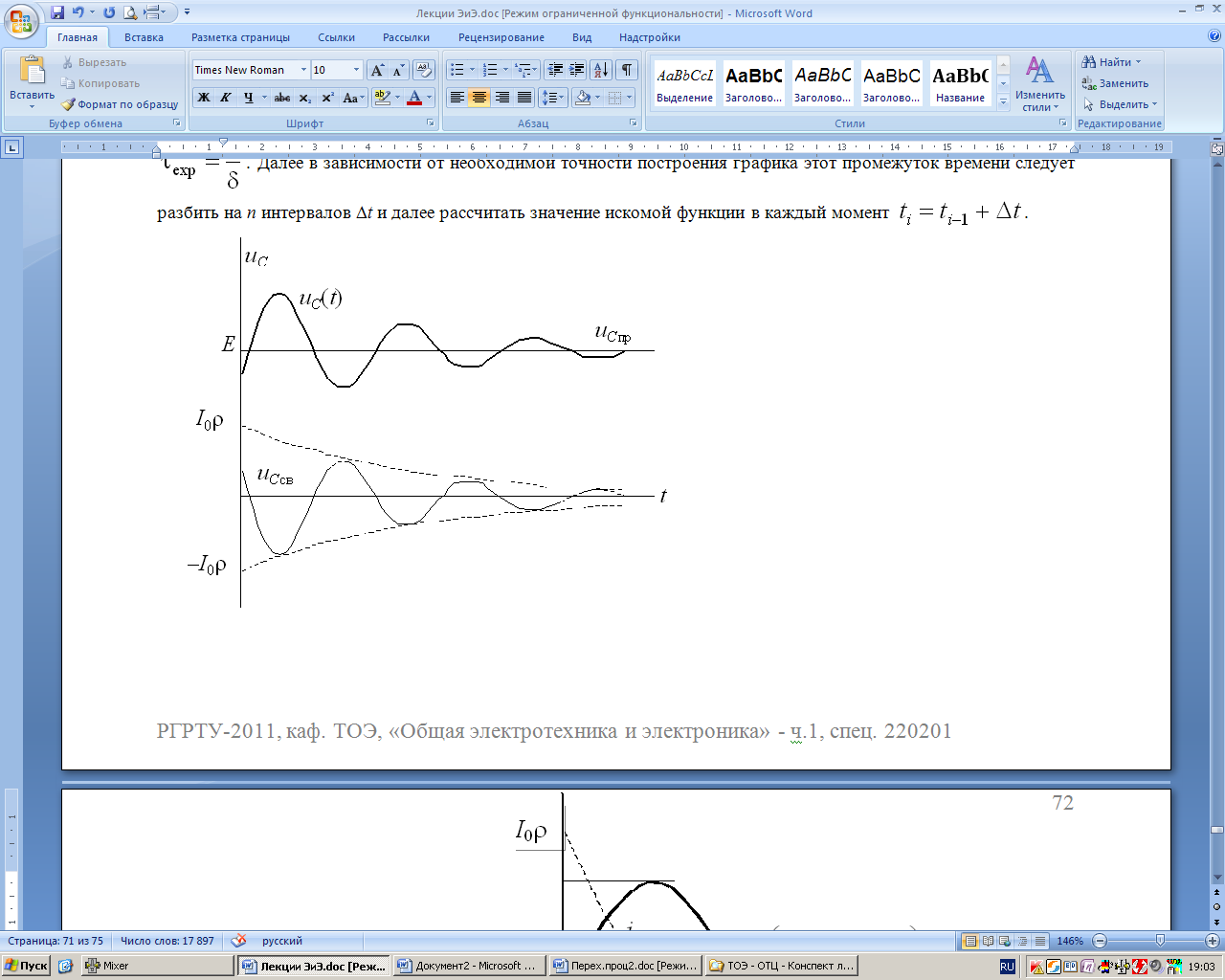
В первых двух случаях переходный процесс носит апериодический характер (напряжение на емкости uC монотонно затухает до нуля, не меняя своей полярности); в третьем случае процесс разряда – колебательный.
8.2.6.2 Апериодический разряд емкости на цепь rl
Рассмотрим
случай, когда p1,2
– действительные
и отрицательные,
т.е.
![]() .
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
.
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
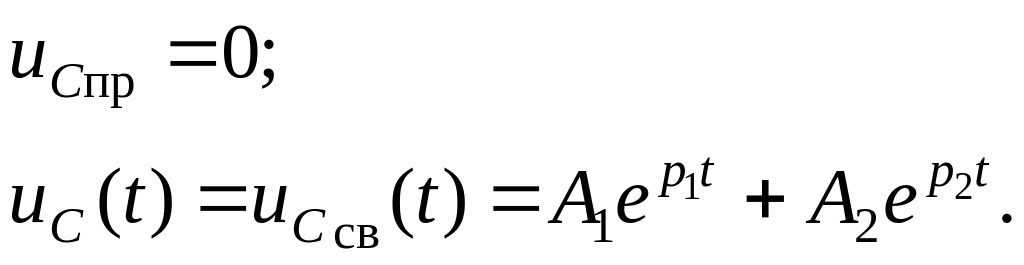
Найдем постоянные интегрирования А1 и А2:
![]() ;
;
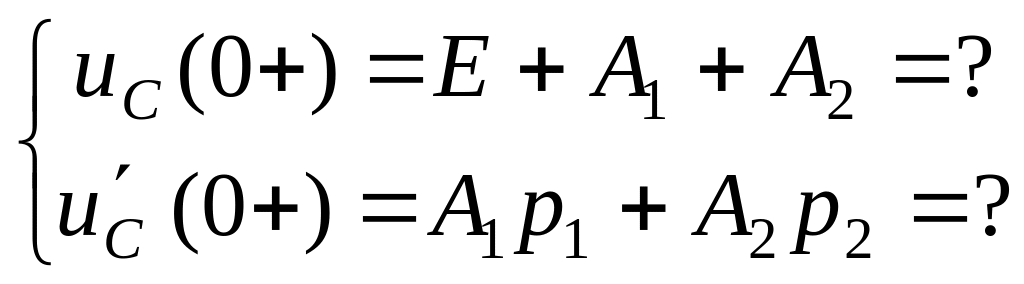
![]()
![]()
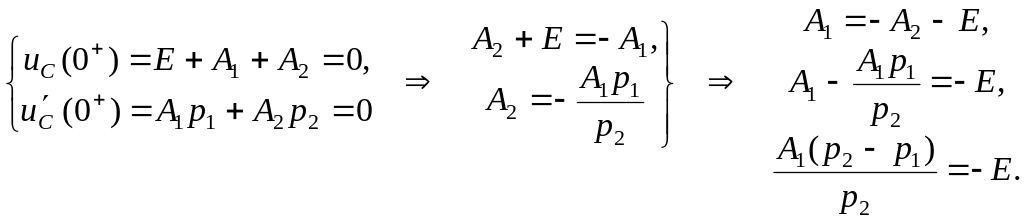
![]() ;
аналогично:
;
аналогично:
![]() .
.
Таким
образом, искомое
![]() имеет
вид:
имеет
вид:
![]() .
.
![]() ;
;
![]() .
.
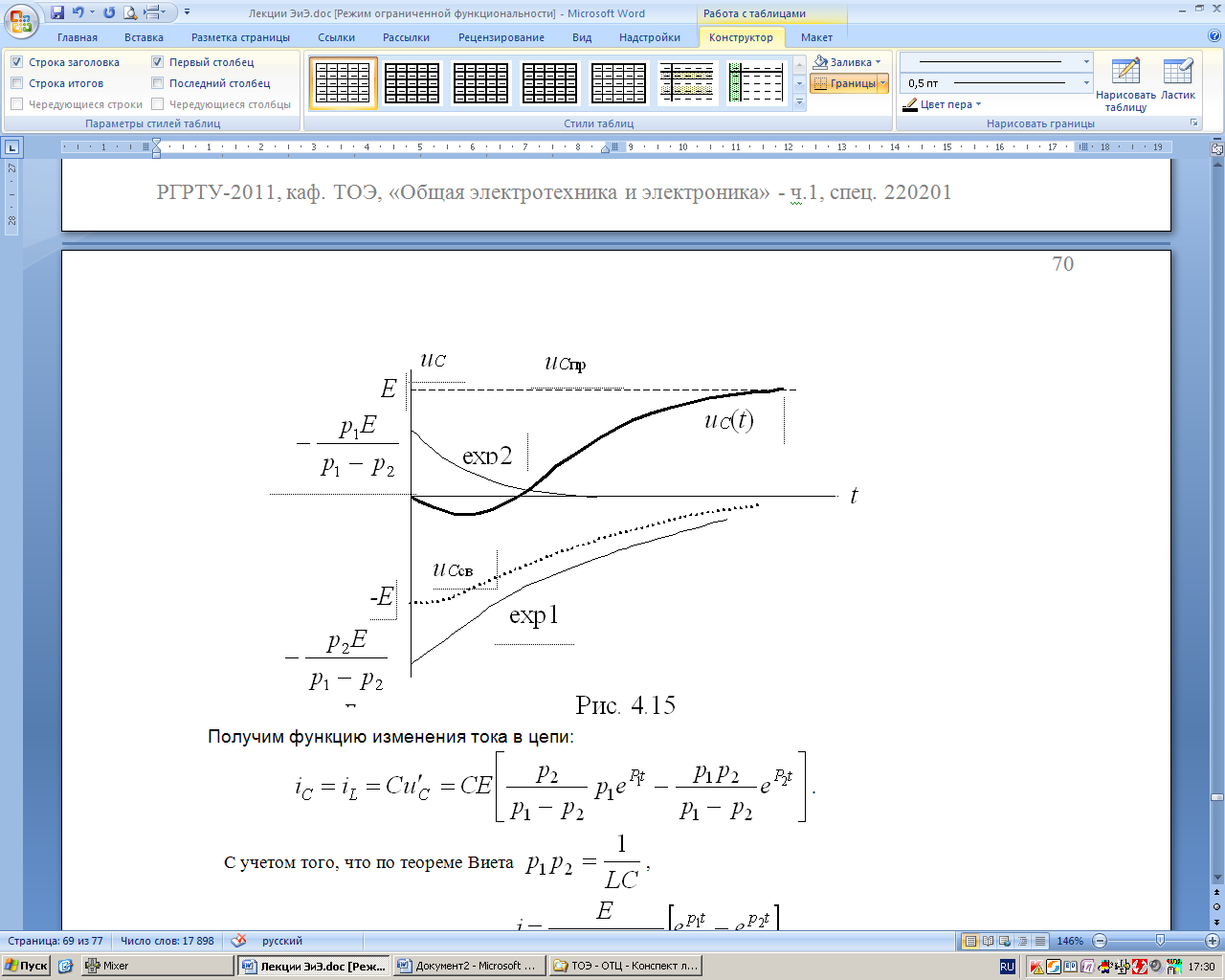
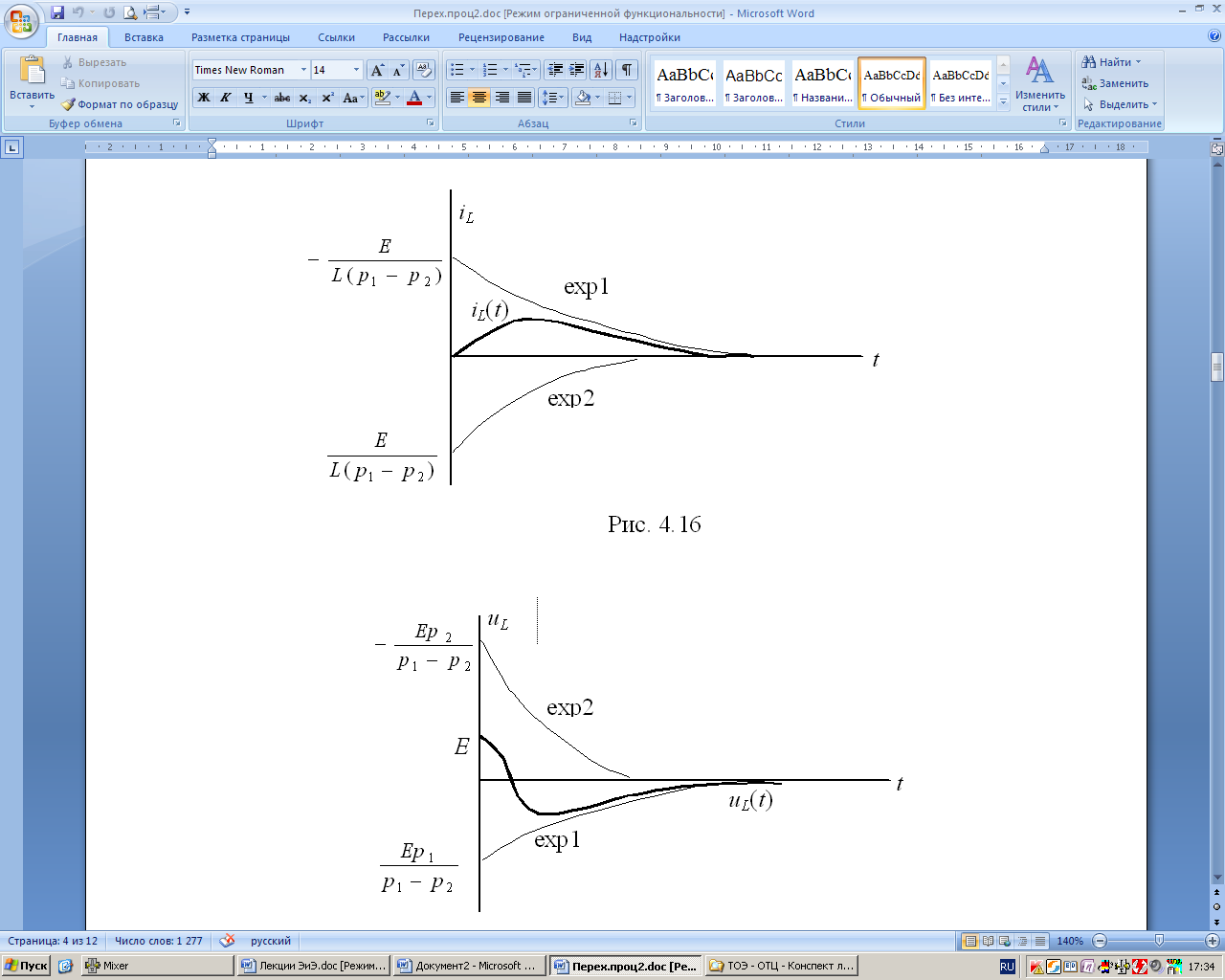
Качественно изобразим график (рис. 8.15).
Рис. 8.15 |
Рассмотрим начальные значения:
|
Получим функцию изменения тока в цепи:
![]() .
.
С
учетом того, что по теореме Виета
![]() ,
,
![]() .
.
Для
построения графика (рис. 8.16) проведем
аналогичные изложенным выше исследования.
Поскольку
![]() ,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
![]() ,
,
![]() ,
,
![]() ,
тогда
,
тогда
![]()
Получим функцию изменения напряжения на индуктивности
![]() .
.
С учетом сказанного выше, exp1 находится в нижней полуплоскости и имеет большую постоянную времени, а exp2 находится в верхней полуплоскости и устремляется к нулю за меньший промежуток времени (рис. 8.17).
Начальные
условия определяются следующим образом
![]() .
Поскольку
,
модули exp 1, 2
отличаются на E, причем exp1(0+) < exp2(0+).
.
Поскольку
,
модули exp 1, 2
отличаются на E, причем exp1(0+) < exp2(0+).
Рис. 8.16 |
Рис. 8 .17 |
8.2.5.3 Колебательный заряд конденсатора
В
случае, если корни характеристического
уравнения p1,2
комплексные сопряженные, переходный
процесс имеет колебательный
характер. В
данном случае
![]() и подкоренное выражение отрицательное.
Корни характеристического уравнения
в общем случае записываются в виде
и подкоренное выражение отрицательное.
Корни характеристического уравнения
в общем случае записываются в виде
![]() ,
,
где
![]() –
коэффициент затухания;
–
коэффициент затухания;
![]() – частота
свободных (собственных) колебаний
контура.
– частота
свободных (собственных) колебаний
контура.
Между
![]() и
и
![]() существует следующая связь
существует следующая связь
![]() .
.
Поскольку все изложенные выше выкладки применимы и для данного случая, запишем полное решение
![]() .
.
Подставив
в данную формулу выражения для
![]() и
и
![]() ,
получим:
,
получим:
![]() .
.
Определим ток в контуре
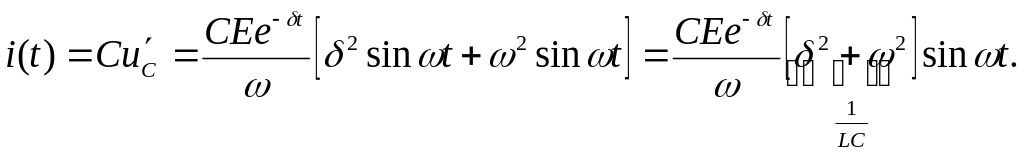
Таким
образом,
![]() .
.
Введем
![]() и упростим выражение, полученное для
:
и упростим выражение, полученное для
:
![]() .
.
При
построении
графиков
следует принимать во внимание соотношение
между постоянной времени экспоненты
![]() и периодом синусоиды
и периодом синусоиды
![]() в свободной составляющей. Рассмотрим
два варианта.
в свободной составляющей. Рассмотрим
два варианта.
1. ![]() .
В данном случае возможно графическое
перемножение экспоненты
.
В данном случае возможно графическое
перемножение экспоненты
![]() и синусоиды
и синусоиды
![]() (рис. 8.18).
(рис. 8.18).
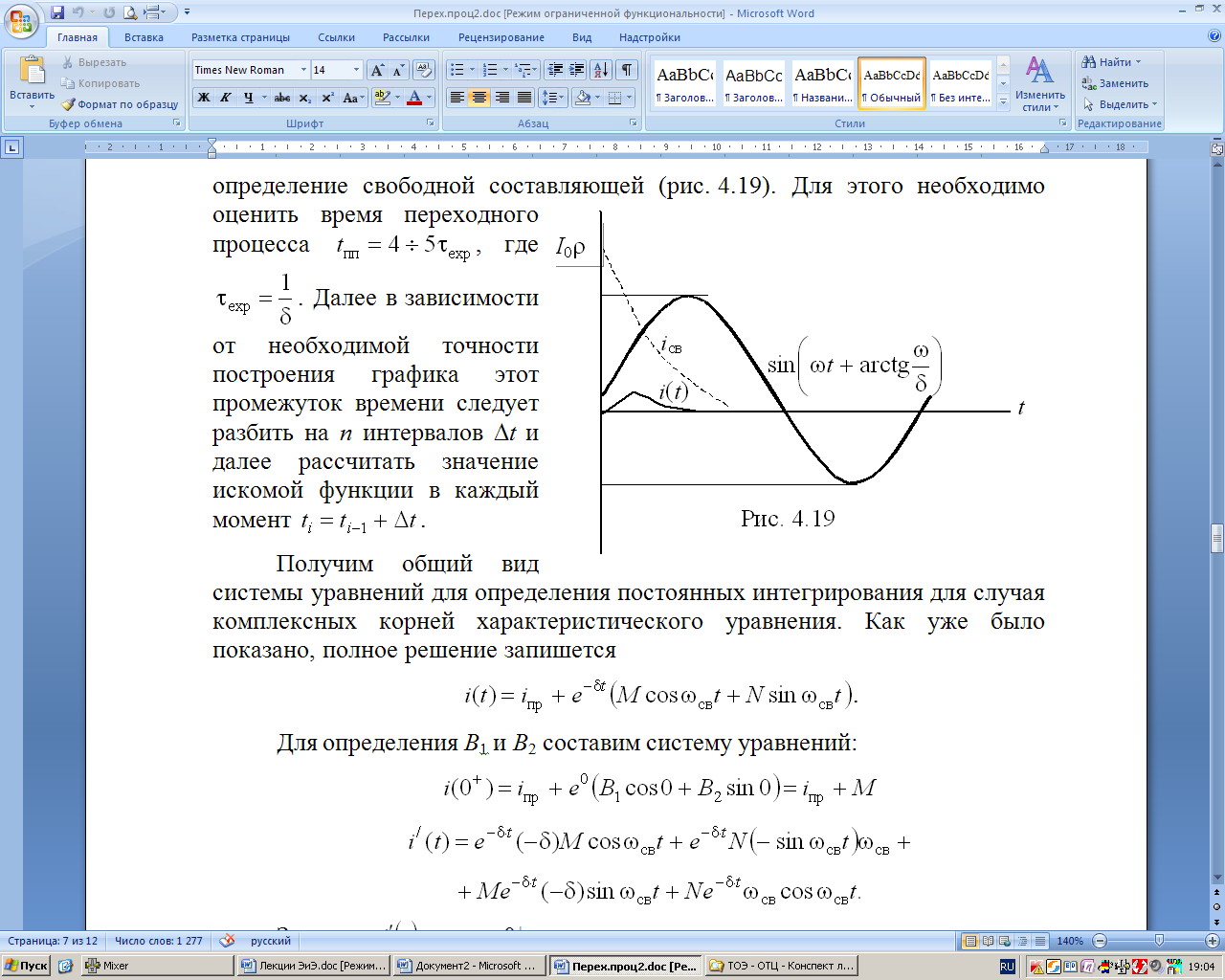
2. ![]() .
В данном случае возможно только
аналитическое определение свободной
составляющей (рис. 8.19). Для этого
необходимо оценить время переходного
процесса
.
В данном случае возможно только
аналитическое определение свободной
составляющей (рис. 8.19). Для этого
необходимо оценить время переходного
процесса
![]() ,
где
,
где
![]() .
Далее в зависимости от необходимой
точности построения графика этот
промежуток времени следует разбить на
n интервалов t
и далее рассчитать значение искомой
функции в каждый момент
.
Далее в зависимости от необходимой
точности построения графика этот
промежуток времени следует разбить на
n интервалов t
и далее рассчитать значение искомой
функции в каждый момент
![]() .
.
Рис. 8.18 |
Рис. 8.19
|
Получим общий вид системы уравнений для определения постоянных интегрирования для случая комплексных корней характеристического уравнения. Как уже было показано, полное решение запишется
![]() .
.
Для определения В1 и В2 составим систему уравнений:
![]()
![]()
![]()
Запишем
![]() для t
= 0+
для t
= 0+
![]()
Таким образом, искомая система уравнений имеет вид: