Определение величины ошибки при прямых измерениях

Пусть, измеряя некоторую величину х, мы получим серию результатов х₁, х₂, х₃,..... х_n. Которое из этих значений является наиболее близким к истинному?

Теория ошибок указывает, что наиболее близким к истинному значению измеряемой величины будет среднее арифметическое значение ряда отдельных измерений, т. е.

.

Причем, при n, x_срх_ист.

При вычислении среднего арифметического измеряемого значения ошибки в сторону увеличения и уменьшения величины наилучшим образом компенсируют друг друга. Величина

называется отклонением данного i-того измерения от среднего.

Абсолютная величина наибольшего из этих отклонений определяет границы интервала значений искомой величины.

Предположим, при измерении величины x мы получим ряд значений 1,790; 1,795; 1,800; 1,805; 1,810; а пользуясь другим прибором, получим 1,76; 1,78; 1,80; 1,82; 1,84. В обоих случаях среднее значение x = 1,80, но интервалы допустимых значений в первом и во втором случаях не одинаковы и равны соответственно (1,79 1,81) и (1,76 1,84), таким образом, во втором случае он шире.

Если повторять измерение большое число раз, то внутри интервала, ограниченного наибольшими отклонениями, будет располагаться все большее число полученных значений. Если весь интервал разброса разбить на равные участки dх, то большее количество результатов в них будет помещаться на центральных участках, а по мере удаления от центра число результатов, приходящихся на участок dх, будет убывать. Обозначим относительное число всех измерений, приходящихся на участок dх, через , где n - общее число всех измерений. Тогда на единичный отрезок интервала придется относительное число значений .

Если мы вычертим график зависимости от х, то получим кривую, показанную на рис. 1.

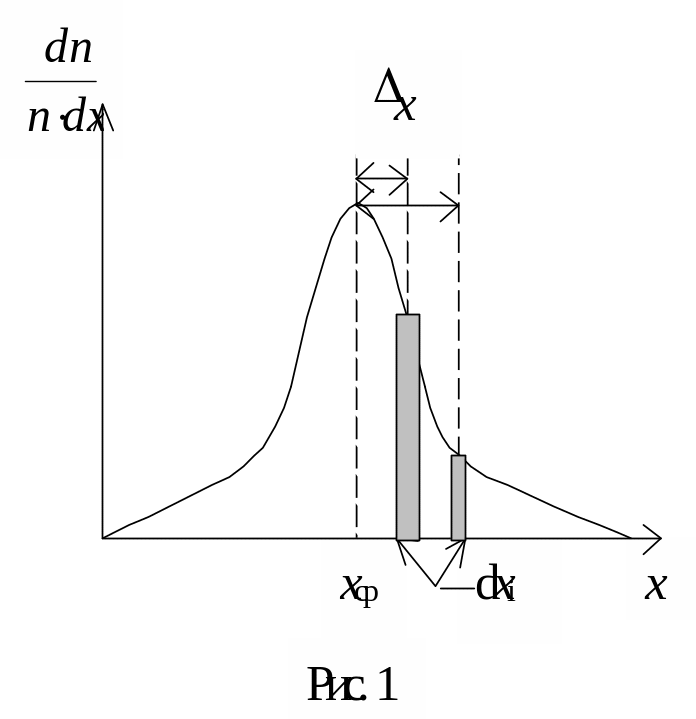
Из рисунка 1 видно, что чем больше участок dх удален от х_ср, тем меньше результатов измерения на него приходится. Не вникая в детали статистической теории погрешности, скажем лишь, что при вид кривой, приведенной на рис. I, хорошо описывается функцией Гаусса

,

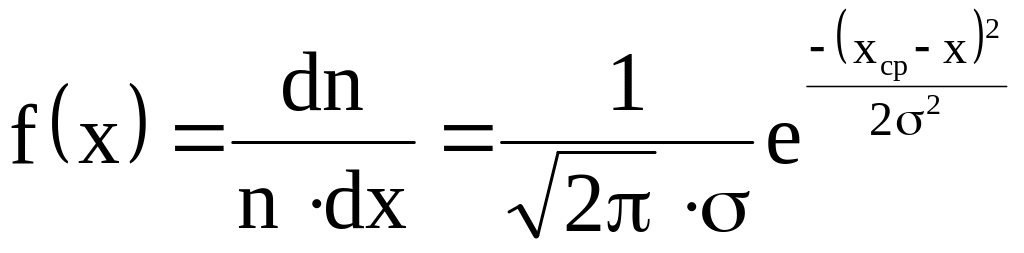где - так называемое среднеквадратичное отклонение, определяющее ширину интервала разброса результатов измерения. Величина определяет вид кривой Гаусса: чем меньше величина , тем быстрее функция стремится к нулю по обе стороны от х_ср. Приближенно можно считать, что полуширина кривой Гаусса на ее полувысоте равняется . Наилучшим приближением к является величина S, которую называют среднеквадратичной ошибкой отдельного измерения:

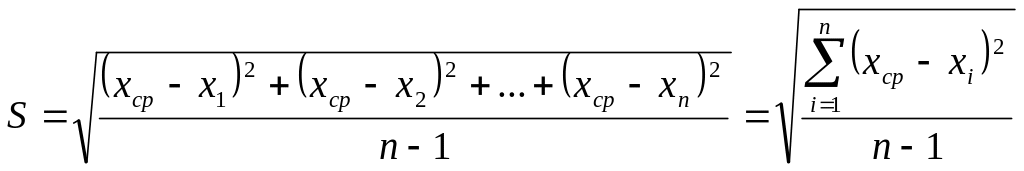
при .

Если мы провели не одну, а несколько серий (m – серий) измерений и в каждой получили среднеарифметическое значение х_ср.к (где к – номер серии ), то эти значения также распределились вокруг искомого х_ист, но уже с меньшим разбросом, который характеризовался бы среднеквадратичной ошибкой среднего . связано с простым соотношением

.

Отсюда, считая S хорошим приближением для , получим

или .

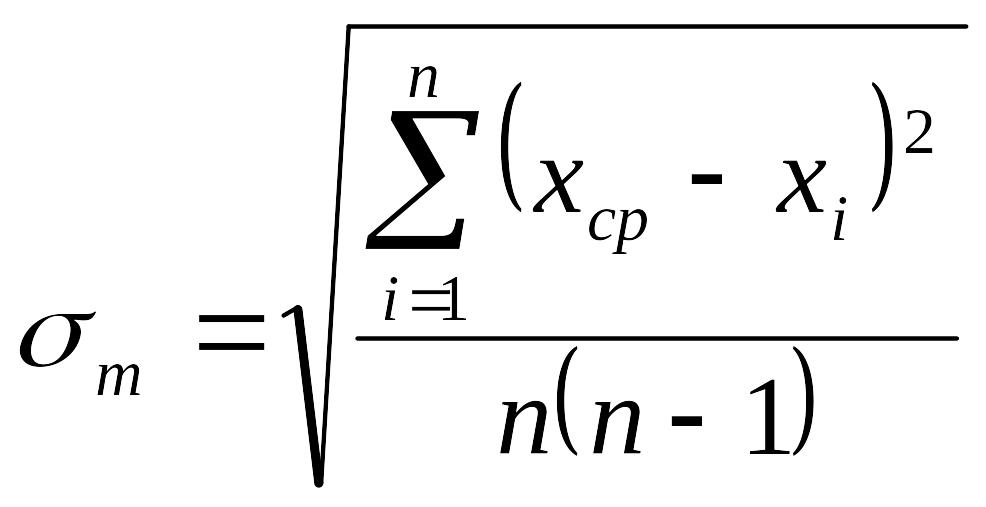Истинное значение измеряемой величины принципиально недостижимо, за исключением редких случаев Величина определяет максимальные границы разброса полученных значений; внутри интервала х_ср  _m лежит лишь около 68% всех измеренных значений, т. е. вероятность попадания искомой величины в данный интервал составляет 68% или 0,68. Эта величина носит название доверительной вероятности (коэффициента надежности), а сам интервал х_ср  _m – называется доверительным интервалом. Величина  возрастает от 95 % или 0,95 внутри интервала х_ср  2_m и до 99,7 % или 0,997 внутри интервала х_ср  3_m.

х_ср-σ_m х_ср х_ср+σ_m

2σ_m

Однако все эти рассуждения справедливы лишь в случае точно заданной величины . Так как мы используем вместо лишь его приближенное значение S и ограничиваемся сравнительно небольшим числом измерений, то определение ширины доверительного интервала, внутри которого с определенной вероятностью находится искомое значение:

х = t_n _m,

будет определяться коэффициентом t_n, зависящим как от числа проведенных измерений (n), так и заданной доверительной вероятностью ( ). Эти коэффициенты – коэффициенты Стьюдента (такой псевдоним принял английский химик Госсет) рассчитаны для различных n и и приводятся в таблицах.

Так, для n = 5 и = 0,95 = 2,8, а ширина доверительного интервала . Эта величина и должна приводиться в качестве ошибки.

Значение коэффициентов Стьюдента приводится в Таблице 1.

Таблица №1