Лабораторная работа № 7 изучение динамики поступательного и вращательного движения на установке

“МАШИНА АТВУДА”

Цель: Определение ускорения поступательного движения грузов на машине Атвуда, момента сил трения в подшипнике, работы сил трения при движении грузов, времени запаздывания при срабатывании фрикциона.

Теоретические основы работы

Л абораторная установка, называемая машиной Атвуда, предназначена для изучения динамики поступательного и вращательного движения, закона сохранения механической энергии.

Машина Атвуда (рис.7.1) состоит из двух грузов одинаковой массы m, связанных нерастяжимой нитью. Нить перекинута через блок, укрепленный на кронштейне. Массой нити можно пренебречь. Если поместить на один из грузов перегрузок массой m₀, то система придет в движение. Сменный блок может быть легким (m_бm) или иметь массу m_б, сопоставимую по порядку величины с массой m. Груз с перегрузком поднимают на высоту h (см. рис. 7.1) и затем отпускают. Измеряется время движения груза с высоты h.

Поступательное движение грузов и перегрузка можно описать с помощью второго закона Ньютона. Для левого груза закон в проекции на ось 0у дает

(7.1)

для правого груза с перегрузком получаем соответственно

(7.2)

Для случая m_бm имеет место равенство Т₁= Т₂= Т. В этом случае решение системы уравнений (7.1), (7.2) дает значение ускорения а_т, с которым движутся грузы m и m+m₀:

(7.3)

Если ускорение свободного падения неизвестно, то значение можно определить из кинематических соображений.

Уравнение движения груза в проекции на ось 0у имеет вид

.

С учетом начального условия (0=0) получим

. (7.4)

Если блок имеет массу m_б, соизмеримую с массой грузов (массивный блок), то его движение можно описать, используя основное уравнение динамики вращательного движения относительно неподвижной оси. Для установки, изображенной на рис.7.1, уравнение динамики вращательного движения относительно оси 0z, перпендикулярной плоскости листа и направленной "от нас", принимает вид

-М_тр - Т₂R_б + Т₁R_б =  I (7.5)

Здесь М_тр- момент сил трения; R_б- радиус блока; I- момент инерции блока относительно оси вращения 0z.

Определение ускорения поступательного движения груза на машине Атвуда

Постановка задачи. Определить ускорение движения грузов в машине Атвуда, если известно, что правый груз с перегрузком опускается с высоты h₁ за время ₁, а с высоты h₂ за время ₂. Учесть, что запуск машины Атвуда происходит с запаздыванием, поэтому отсчет времени в установке начинается раньше, чем движение грузов.

Указания к решению. Запишем кинематические уравнения движения левого груза для двух пройденных расстояний h₁ и h₂:

(7.6)

Здесь ₀-время запаздывания при срабатывании фрикциона; а_э- ускорение грузов, определяемое из эксперимента. Для исключения времени запаздывания ₀ измерение времени движения производят для двух значений h₁ и h₂. Решая систему уравнений (7.6), получим

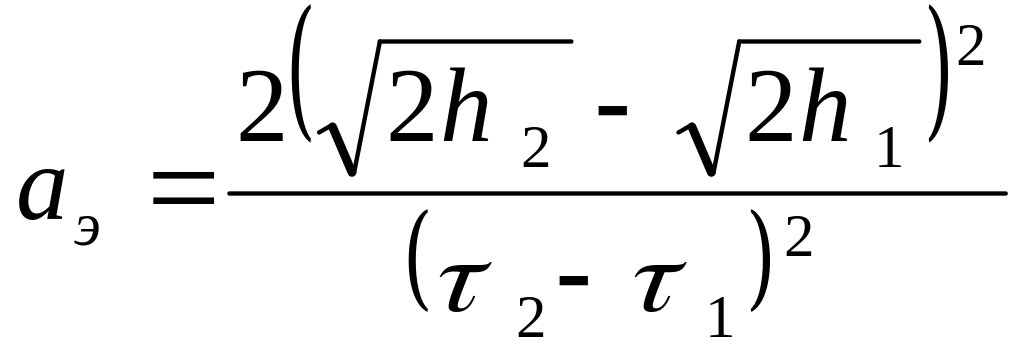(7.7)

Установка «Машина Атвуда» в имеющейся модификации позволяет определить время движения груза после снятия перегрузка (между фотодатчиками). Это участок равномерного движения.

1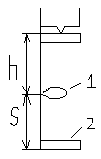 – кольцо с верхним фотодатчаком

2 – нижний фотодатчик

Тогда средняя скорость на нижнем участке:

равна конечной скорости на верхнем участке , т.е.

.

Учитывая это, можно записать: .

Отсюда - эта формула связывает время  прохождения верхнего участка (движение с ускорением) и время t, фиксируемое миллисекундомером. В формулу (7.7) входит время .