2.3. Связность

Def. Говорят, что вершина u достижима из v, если существует маршрут, соединяющий u и v.

Def. Граф называется связным, если любые его две вершины можно соединить маршрутом.

Замечание. Учитывая свойство 1 маршрутов, в этих определениях слово “маршрут” можно заменить на “простая цепь”.

Теорема 2.3. (1-я теорема о связности) Для связности графа необходимо и достаточно, чтобы в нем какая-нибудь фиксированная вершина u была достижима из любой другой вершины.

Доказательство. Пусть вершина u достижима из любой другой вершины. Выберем две любые вершины v и w. Соединим v и u, а также w и u маршрутами. Объединив их, получим маршрут v, u, w, соединяющий вершины v и w. В силу произвольности v и w, теорема доказана.

Компоненты связности

Задание. Доказать, что отношение достижимости между двумя вершинами обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является эквивалентностью.

Так как отношение достижимости между двумя вершинами является эквивалентностью, то, по теореме о разбиении, вершины графа можно разбить на непересекающиеся классы V₁, …, V_k, и такие, что вершины, принадлежащие одному классу достижимы друг для друга, но не достижимы для вершин из любого другого класса.

Образуем подграфы G_i = (V_i, E_i), соединив вершины множества V_i ребрами из множества E_i  E. Очевидно – граф распался на связные подграфы, не имеющие общих вершин и ребер. Такие подграфы называются компонентами связности графа G. Геометрически они выглядят, как отдельные изолированные куски.

Теорема 2.4. (2-я терема о связности) Если в произвольном неориентированном графе ровно две вершины имеют нечетную степень, то они достижимы друг для друга.

Доказательство. Пусть в графе G только две вершины u и v имеют нечетную степень. По теореме 2.2. о нечетных степенях, в конечном графе число вершин с нечетными степенями четно. Пусть G_u – компонента связности, которой принадлежит вершина u. Так как теорема 2.2 применима и к G_u , то в ней кроме u должна быть еще хотя бы одна вершина с нечетной степенью. Но во всем графе всего одна такая вершина – это v. Следовательно, v  G_u. Значит, u и v достижимы друг для друга, т.к. принадлежат одной компоненте связности. ЧТД.

Теорема 2.5. (3-я терема о связности) Для n-вершинного графа с m ребрами и k компонентами связности справедливо неравенство m  n – k.

Доказательство. Докажем индукцией по m. При m = 0 будет n = k, значит, неравенство выполняется.

Пусть m > 0 и для графов с меньшим числом ребер неравенство верно. Удалим из графа любое ребро. Тогда число его ребер станет m₁ = m – 1, а число компонент связности либо станет k + 1, либо останется равным k. Рассмотрим два случая.

1) Стало k + 1 компонент. Тогда по предположению индукции m₁ = m – 1  n – (k + 1). Значит m  n – k.

2) Осталось k компонент. Тогда m₁ = m – 1  n – k. Тем более m  n – k.

Теорема доказана.

Лекция № 14 Алгоритмы обхода вершин в графах общего вида

При реализации многих алгоритмов на графах возникает необходимость организовать систематический перебор вершин графа, при котором каждая вершина просматривается точно один раз. Такой перебор можно организовать двумя способами: поиском в глубину или поиском в ширину. При этом программы, реализующие оба поиска, имеют одинаковую структуру и отличаются лишь процедурой, выполняющей перебор вершин.

Основная идея алгоритма поиска в глубину состоит в последовательном движении из заданной вершины вдоль одного из ребер вглубь графа до тех пор, пока не дойдем до вершины, из которой нельзя попасть ни в какую непросмотренную вершину. После этого возвращаемся в предыдущую вершину и повторяем поиск. Если после возврата в начальную вершину останутся непросмотренные вершины, то повторим поиск, начиная из любой оставшейся вершины.

Рис. 3.1

Пусть в каждом списке инцидентности все смежные вершины упорядочены по возрастанию их номеров. Тогда, например, для графа, изображенного на рис. 3.1 последовательность обхода вершин из начальной вершины 1 имеет вид: 1, 2, 4, 5, 3, 5, 6, 5, 4, 7, 4, 2, 1.

Повтор вершин в списке обхода объясняется тем, что во время обратного шага приходится возвращаться в уже просмотренную вершину. Но обработка каждой вершины (т.е. какая-то длительная операция) производится ровно один раз при первом переходе к данной вершине. Поэтому, последовательность обработки вершин для графа рис. 3.1 имеет вид: 1, 2, 4, 5, 3, 6, 7. Если граф является связным, то будут просмотрены все вершины графа.

В алгоритме каждой вершине ставится в соответствие логическая переменная Nowy[v], которая равна True, если данная вершина еще не просмотрена, и False, если вершина просмотрена. Вначале поиска считаем все вершины непросмотренными. Операцию обработки вершины будем символизировать печатью ее номера.

Описанный в алгоритме порядок работы с вершинами, при котором вершина, просмотренная последней, обрабатывается первой, реализуется с помощью механизма стека. Он автоматически реализуется в Паскале рекурсивной процедурой, поэтому рекурсивный вариант алгоритма обычно проще, чем нерекурсивный.

При построении алгоритмов мы будем пользоваться неформальным языком описания алгоритмов. Такой язык по синтаксису похож на язык программирования Паскаль, но он разрешает использование математических обозначений, не предусмотренных в Паскале. Это позволяет сосредоточиться на сути алгоритма и уйти от технических вопросов его реализации. Для реализации алгоритма на одном из языков программирования необходимо формализовать его в соответствии с правилами языка.

Будем использовать обозначения

1) СПИСОК [ v ] – список инцидентности вершины v;

2) for uА – для всех элементов массива А.

Опишем рекурсивную процедуру.

procedure DEPTH_R(v) ;

begin NOWY[v]:= False; write(v) ;

for u  СПИСОК[v] do

if NOWY[u] then DEPTH_R(u) ;

end ;

Основная программа поиска имеет вид.

var NOWY : array [1..n] of boolean;

begin for vV do NOWY[v]:= True ;

for vV do

if NOWY[v] then DEPTH_R(v)

end.

В первом цикле программы производится инициализация массива Nowy. Далее для первой непросмотренной вершины вызывается процедура поиска. Если граф – связный, то после возврата в основную программу поиск будет закончен. В противном случае при первом вызове процедуры DEPTH_R будут просмотрены все вершины одной компоненты связности графа, затем поиск повторится, начиная с первой непросмотренной вершины. Таким образом, обращение к процедуре DEPTH_R(v) из основной программы происходит всякий раз при переходе к очередной компоненте связности графа.

Например, рассмотрим несвязный граф.

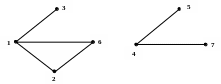
Рис. 3.2

Начнем поиск с начальной вершины 1. При вызове процедуры DEPTH_R(1) получаем следующую последовательность вершин: 1, 2, 6, 3, после чего происходит выход из процедуры в основную программу, т.к. список смежности исходной вершины исчерпан. При следующем вызове процедуры просмотр начнется с первой непросмотренной вершины 4, принадлежащей следующей компоненте связности графа.

Таким образом, для произвольного графа алгоритм работает корректно, то есть будут просмотрены все вершины графа, причем каждая не более одного раза.

Оценим вычислительную сложность рекурсивного варианта алгоритма. В качестве основной операции, по числу выполнений которой определяется трудоемкость алгоритма, выберем вызов процедуры DEPTH_R.

В основной программе она вызывается не более n раз. Внутри самой процедуры ее вызов в каждой вершине осуществляется столько раз, сколько эта вершина имеет смежных, или сколько ребер ей инцидентны. Так как каждое ребро инцидентно двум вершинам, то число вызовов не более 2m. Следовательно, вычислительная сложность алгоритма можно оценить как

.

Нерекурсивный поиск. Приведем нерекурсивный вариант процедуры поиска в глубину, использующий механизм стека, который организуется программистом (“вручную”). Обычно такой вариант требует меньше памяти и работает быстрее, чем рекурсивный, хотя и сложнее по реализации.

Всюду в дальнейшем мы будем использовать следующие обозначения:

1. СТЕК  v, ОЧЕРЕДЬ  v – поместить вершину v в СТЕК или ОЧЕРЕДЬ;

2. v  СТЕК; v  ОЧЕРЕДЬ – извлечь вершину v из СТЕКА или ОЧЕРЕДИ.

3. top(Массив) – первый элемент массива (стека, списка или иного).

4. down(Массив) – последний элемент массива.

5. x:= top(СТЕК) – переписать в переменную х первый элемент стека, не извлекая его.

6. Next(Массив) – следующий по порядку элемент массива.

procedure DEPTH( v );

begin СТЕК:= ; СТЕК  v;

NOWY[v]:= False; write(v); {вершина просмотрена}

while СТЕК<> do

begin t:=top(СТЕК);

P:= top(СПИСОК[t]);

while(P<>down(СПИСОК[t]))and(not Nowy[P])

do P:= Next(СПИСОК[t]);

if P<>down(СПИСОК[t])then

{найдена новая вершина}

begin t:=P; СТЕКt; NOWY[t]:= False;

Write (t)

end

else {вершина t использована}

t  СТЕК,

end

end;

Головная программа имеет такую же структуру, что и для рекусивного варианта.

Алгоритм поиска в ширину(очередь – queue)

Основная идея такого поиска – последовательный просмотр списков инцидентности вершин, смежных с данной. При поиске в ширину, попав в новую вершину, просматривают все смежные с ней непросмотренные вершины и заносит их в список, после чего эта вершина считается обработанной. Далее переходят в новую вершину, стоящую первой в списке необработанных вершин. Иными словами, просмотр осуществляется по принципу очереди: чем раньше вершина просмотрена, тем раньше она будет обработана.

Например, для графа, изображенного на рис. 3.1, последовательность просмотра вершин с помощью поиска в ширину имеет вид: 1, 2, 4, 7, 5, 6, 3.

Сложность реализации алгоритма в том, что рекурсивные процедуры действуют по принципу стека, а не очереди. Поэтому в этом случае возможен только нерекурсивный вариант алгоритма.

procedure BREADTH( v ) ;

begin ОЧЕРЕДЬ:=; {ОЧЕРЕДЬ – локальная структура }

ОЧЕРЕДЬ  v; NOWY[v]:= False;

while ОЧЕРЕДЬ <>  do

begin p  ОЧЕРЕДЬ; write(p);

for u  СПИСОК[p] do

if NOWY[u] then

begin ОЧЕРЕДЬ  u;

NOWY[u]:= False

end

end

end;

Как мы уже говорили, основная программа отличается от соответствующей программы поиска в глубину только именем вызываемой во втором цикле процедуры. Аналогично можно показать, что алгоритм корректен, а его вычислительная сложность также равна .