5.4 Метод Ньютона

Итерации по методу Ньютона осуществляются по формуле

. (5.9)

Итерации прекращаются, если выполняется условие (5.6).

Сравнивая формулу (5.9) с формулой итераций (5.5) для метода простой итерации, приходим к выводу, что метод Ньютона – это метод простой итерации с функцией

.

Получаем то же условие сходимости (5.8), что и для метода простой итерации, но с функцией вида

. (5.10)

Условие (5.8) с учетом (5.10) можно записать в виде

. (5.11)

Последнее неравенство должно выполняться для значений на всех возможных итерациях. Детальный анализ условия сходимости (5.11) позволяет сделать вывод, что метод Ньютона сходится, если первоначальное приближение выбрано достаточно близко к корню.

На рисунке 5.4 приведена графическая иллюстрация метода Ньютона. В точке к кривой проводится касательная, точка пересечения которой с осью абсцисс дает нам новое приближение . Затем в точке опять проводится касательная, и т.д.

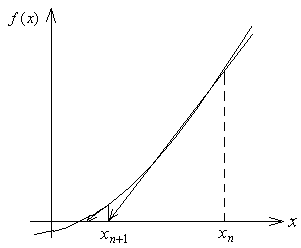
Рисунок 5.4 – Иллюстрация метода Ньютона

Пример. Найдем, как и в примере раздела 5.3, квадратный корень положительного числа , т.е. найдем . Для этого решим уравнение методом Ньютона. В данном случае , , и формула итераций имеет вид

.

5.5 Метод секущих

В методе Ньютона, рассмотренном в разделе 5.4, необходимо знать не только функцию , нуль которой мы ищем, но и производную этой функции , что является недостатком данного метода. Если в методе Ньютона заменить производную на отношение приращений функции и аргумента,

,

то мы получим следующую формулу итераций:

. . (5.12)

Итерации прекращаются, если выполняется условие (5.6). Формула (5.12) называется методом секущих для нахождения корня уравнения (5.1). Графическая иллюстрация метода секущих приведена на рисунке 5.5. Через две точки, определяемые приближениями и , проводится секущая и по ней определяется новое приближение . Затем проводится следующая секущая через точки, определяемые приближениями и , и т.д. В отличие от предыдущих методов этот метод является двухшаговым. Это значит, что для определения нового приближения необходимо иметь два предыдущих приближения.

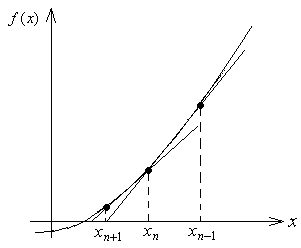
Рисунок 5.5 – Иллюстрация метода секущих

6 Решение обыкновенных дифференциальных уравнений

6.1 Постановка задачи

Соотношение вида

, (6.1)

где – некоторая функция независимой переменной , функции и ее производных , , …, , называется обыкновенным дифференциальным уравнением -го порядка. Решить уравнение – значит найти функцию , превращающую равенство (6.1) в тождество. Существует понятие общего и частного решения этого дифференциального уравнения. Общее решение (общий интеграл) – это формула, дающая все решения данного уравнения. Обычно общее решение обыкновенного дифференциального уравнения -го порядка (6.1) зависит от постоянных , которые могут выбираться произвольно. Решение, которое не зависит от произвольных постоянных, называется частным решением дифференциального уравнения (частным интегралом). График каждого частного решения называется интегральной кривой. Чаще всего для обыкновенного дифференциального уравнения (6.1) формулируется так называемая задача Коши, когда дополнительно к уравнению (6.1) задают значения функции и ее производных до -го порядка в некоторой точке . Эти дополнительные данные называются начальными условиями. Наличие начальных условий позволяет получить частное решение дифференциального уравнения.

Процесс решения дифференциального уравнения называется его интегрированием. Интегрирование дифференциального уравнения вовсе не означает, что этот процесс сводится к вычислению интеграла. Если же решение дифференциального уравнения действительно свелось к вычислению интеграла, то говорят, что уравнение решено в квадратурах.

Методы решения дифференциальных уравнений бывают точные, приближенные и численные. Точные методы дают решение, которое можно выразить в элементарных функциях. Получить точное решение дифференциального уравнения можно не всегда. Например, решение уравнения не выражается в элементарных функциях. Приближенные методы дают решение в виде некоторой последовательности функций , сходящейся к решению при . Численные методы дают решение в виде таблицы значений функции . Мы будем заниматься численными методами решения дифференциальных уравнений. В данной работе рассмотрим методы решения дифференциального уравнения первого порядка

(6.2)

с начальным условием .