2 Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений (СЛАУ) является достаточно важной вычислительной задачей. По сведениям некоторых литературных источников, 75% всех расчетных математических задач приходится на решение СЛАУ. Это понятно, поскольку чаще всего сразу строят наиболее простые математические модели реальных процессов, т.е. линейные модели. С решением СЛАУ связаны такие задачи, как вычисление определителей, обращение матриц, вычисление собственных значений и собственных векторов матриц, интерполирование, аппроксимация по методу наименьших квадратов и многие другие. Современная вычислительная математика располагает большим арсеналом методов решения СЛАУ, а математическое обеспечение ЭВМ – многими пакетами программ и программными системами, позволяющими решать СЛАУ. Поэтому очень важно уметь ориентироваться в этом море методов и программ с тем, чтобы выбрать для себя наиболее подходящие или даже предложить собственные их модификации.
2.1 Постановка задачи. Методы решения
Определение. Системой линейных алгебраических уравнений (СЛАУ) называется совокупность равенств вида
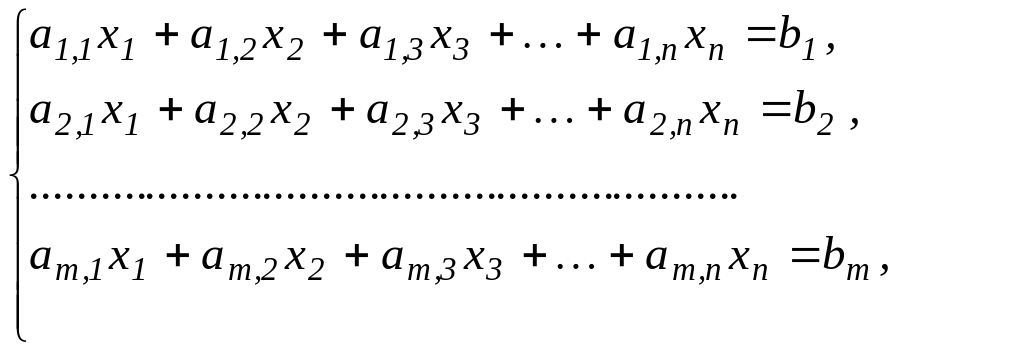(2.1)
которые
при некоторых значениях переменных
могут обращаться в тождества.
Переменные
этой совокупности равенств называются
неизвестными, переменные
,
– коэффициентами, а переменные
,
– свободными членами СЛАУ. Значения
переменных
,
которые обращают равенства (2.1) в
тождества, называются решением СЛАУ.
Таким образом, задача решения СЛАУ
состоит в том, чтобы по известным
коэффициентам системы
,
и свободным членам
,
найти значения переменных
,
обращающие равенства (2.1) в тождества.
СЛАУ
вида (2.1) – это система
уравнений с
неизвестными. Не останавливаясь на
общей теории таких систем уравнений, в
дальнейшем ограничимся рассмотрением
системы
уравнений с
неизвестными
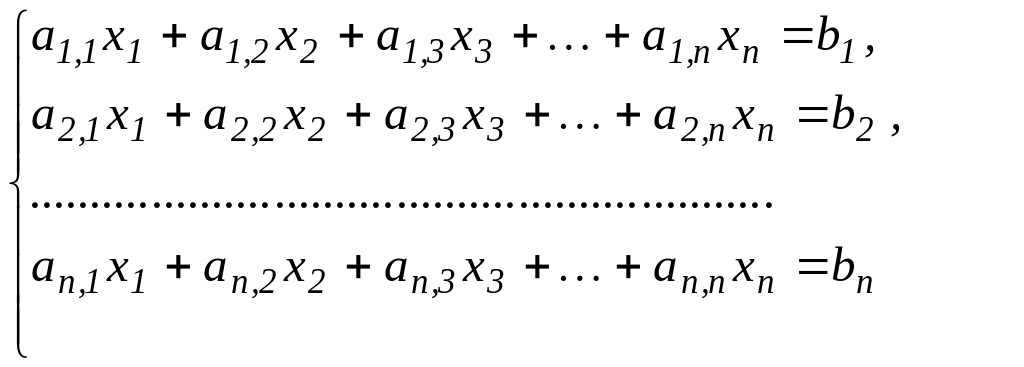(2.2)
Эту систему уравнений можно записать в краткой форме:
,
,
.
(2.3)
Часто
систему (2.2) записывают в векторно-матричной
форме. Для этого вводят в рассмотрение
(
)-матрицу
коэффициентов
и векторы-столбцы неизвестных
и свободных членов
,
,
:
,
,
.
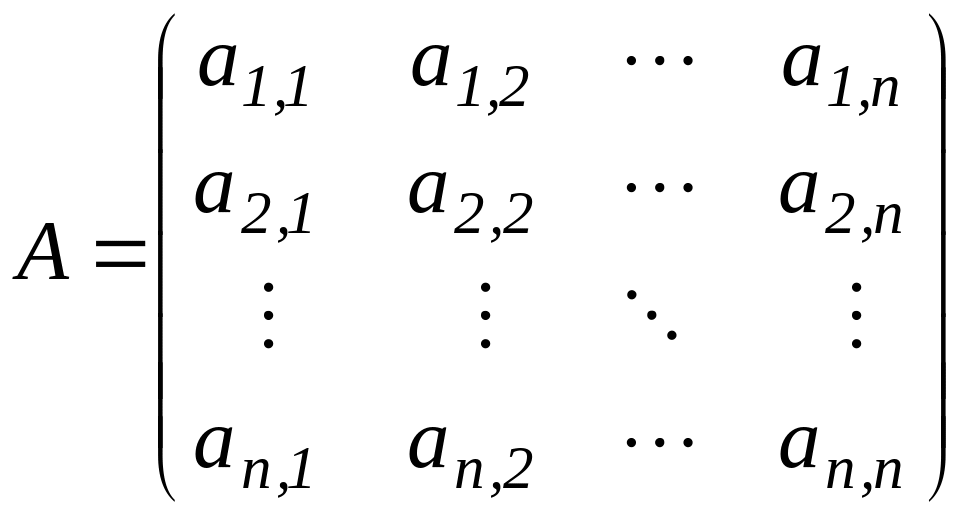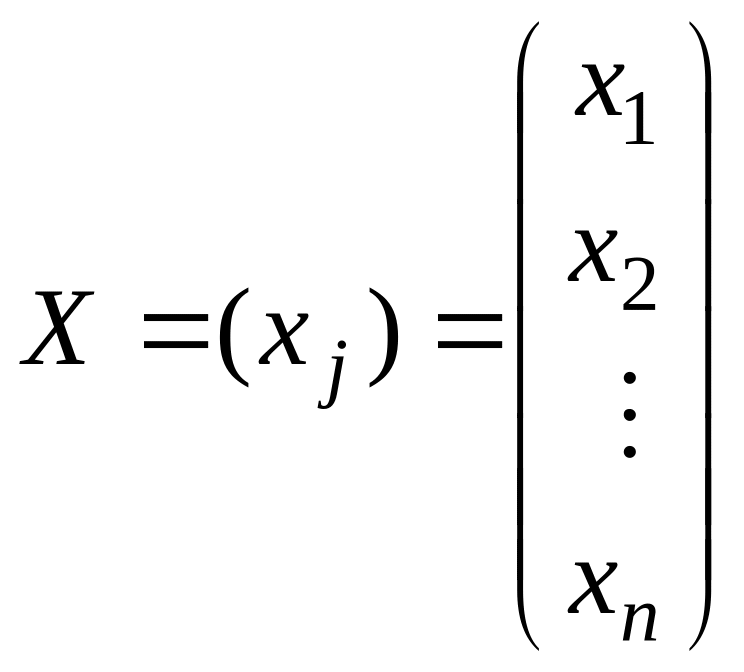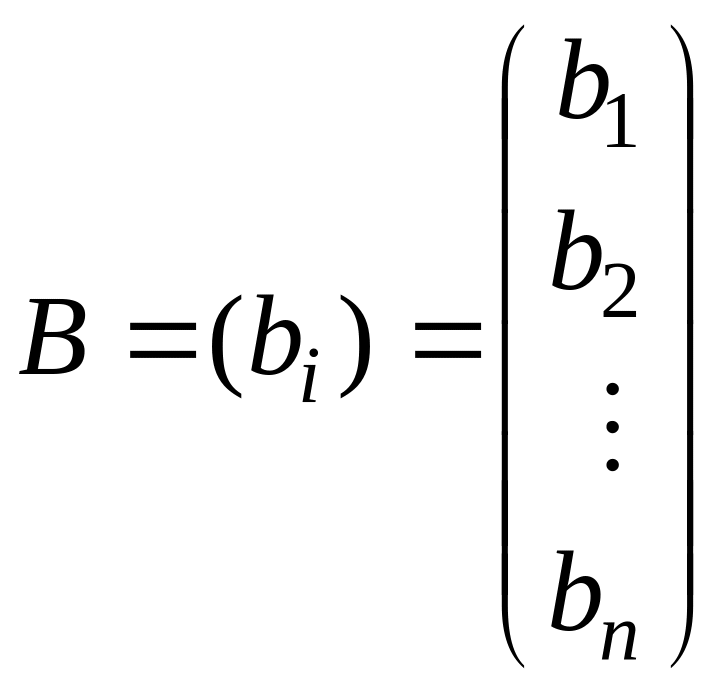Тогда СЛАУ (2.2) записывается в виде
,
(2.4)
поскольку
сумма в левой части выражения (2.3) есть
формула для расчета элементов матрицы
.
Если
определитель матрицы
не равен нулю (
),
то система (2.2) (или (2.4)) имеет единственное
решение, которое определяется формулой
,
(2.5)
где
– матрица, обратная матрице
.
Известно также правило Крамера для
решения СЛАУ (2.4), в соответствии с которым
неизвестные определяются по формуле:
,
(2.6)
где
– определитель матрицы
,
а
– определитель матрицы
,
в которой столбец коэффициентов при
заменен столбцом свободных членов.
Однако методы решение СЛАУ с помощью обратной матрицы (2.5) или с помощью правила Крамера (2.6) встречают возражения с различных сторон. Прежде всего отмечается их большая трудоемкость (вычислительная сложность).
Если
при реализации формул Крамера определители
вычислять путем понижения порядка, т.е.
путем разложения по элементам какой-нибудь
строки или какого-нибудь столбца, то на
вычисление определителя потребуется
операций умножения, а на решение СЛАУ
–
таких операций. Факториальный рост
количества арифметических операций с
увеличением размерности задачи (и вообще
очень быстрый рост) называется «проклятьем
размерности». По оценке работы [3] число
операций
недоступно для современных ЭВМ. Если
оценить величину
и прикинуть потенциальные возможности
развития вычислительной техники, то
можно сделать вывод о том, что в обозримом
будущем системы сотого порядка в принципе
не могут быть решены по формулам Крамера
[4]. Вместе с тем размерность
или
для современных задач считается
небольшой. Довольно часто приходится
решать системы с тысячами и более
переменных.
Если решение находить с помощью обратной матрицы по формуле (2.5) и обратную матрицу находить через алгебраические дополнения, то такое решение СЛАУ будет равнозначным применению формул Крамера с теми же недостатками.
Другой причиной, по которой классические методы считаются неприемлемыми, является сильное влияние на окончательный результат округлений: погрешности за счет округлений катастрофически нарастают с увеличением числа переменных .
В связи с указанными недостатками классических методов разработаны и применяются другие методы решения СЛАУ. Вообще все методы решения СЛАУ можно разделить на конечные и итерационные. Конечные методы называются также точными. Точные методы – это методы, которые в условиях отсутствия округлений приводят к точному решению за конечное число арифметических и логических операций. Итерационные методы – это методы, которые в условиях отсутствия округлений могут привести к точному решению путем бесконечного повторения единообразных действий (итераций). Понятно, что при наличии округлений и точные, и итерационные методы приведут к приближенному решению.
Точными следует считать метод решения путем обращения матрицы СЛАУ, правило Крамера, а также рассматриваемый в разделе 2.2 метод исключения Гаусса. Рассматриваемый в разделе 2.5 метод Гаусса-Зейделя является итерационным.