
Винтовые поверхости
.docx|
ВИНТОВЫЕ ПОВЕРХНОСТИ. |
Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.
|
|
При этом поступательное и угловое перемещение находятся в определенной зависимости ∆h=k∆v, где ∆h – линейное перемещение за время ∆t, ∆v – угловое перемещение за то же время, k – коэффициент пропорциональности. Если k=Const, то шаг поверхности постоянный. Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит из двух линий: образующей m, и оси i (рис.8.12). Алгоритмическая часть: 1. На образующей m выделяют ряд точек А, В, С, … 2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки. |
|
|
|
|
|
Винтовые поверхности
Поверхность называется винтовой, если она получается винтовым перемещением образующей.
* Поверхность однополостного гиперболоида вращения относится также к классу линейчатых поверхлостей. Она может быть получена путем вращении прямой вокруг оси, скрещивающейся с ней
** Винтовое перемещение характеризуется вращением вокруг оси и одновременным поступательным движением, параллельным этой оси.
Н зависимости от формы образующей отдельные виды винтовых поверхностей могут быть отнесены как к классу линейчатых, так и не линейчатых поверхностей. Выделение этих поверхностей в самостоятельный подкласс связано со стремлением подчеркнуть значение винтовых поверхностей в технике, архитектурно-строительной практике и, особенно, в машиностроении.
Характерной особенностью для винтовых поверхностей с постоянным шагом является постоянство угла tp° наклона прямолинейной образующей к направляющей плоскости, за которую принята плоскость, перпендикулярная оси винтовой поверхности.
Как уже неоднократно отмечалось, для получения наглядного изображения поверхности (в частности, винтовой) ее задание проекциями геометрической части определителя следует расширить до задания каркасом, состоящим из двух семейств линий: семейства направляющих (винтовых параллелей) * и семейства, составленного из последовательных положений прямолинейных образующих.
Винтовая линия постоянного шага, построенная на поверхности прямого кругового цилиндра, называется гелисой. Поэтому линейчатые винтовые поверхности, направляющая которых — гелиса, называются геликоидами. В зависимости от величины угла наклона образующей к оси геликоиды бывают прямыми, если этот угол равен 90°, и косыми (наклонными), если угол — произвольный, отличный от 0 и 90° .
В свою очередь, прямые и косые геликоиды подразделяются на закрытые и открытые. Признаком для такого деления служит взаимное расположение оси геликоида и его образующей. Если образующая и ось пересекаются, геликоид называют закрытым, если скрещиваются - открытым.
Следует отметить одно важное свойство винтовых поверхностей, состоящее в том, что эти поверхности, так же как и поверхности вращения, могут сдвигаться, т. е., совершая винтовое перемещение, поверхность скользит вдоль самой себя. Это свойство обеспечивает винтовым поверхностям широкое применение в технике. Винты, шнеки, сверла, пружины, поверхности лопаток турбин и вентиляторов, рабочие органы судовых движителей, конструкции винтовых аппарелей и лестниц — вот далеко не полный перечень технического использования винтовых поверхностей.
|
Винтовые поверхности - Цилиндроид и Коноид |
|
|
В разделе начертательной геометрии были рассмотрены наиболее распространенные в технике поверхности кругового цилиндра, кругового конуса, шара, прямой призмы, пирамиды. Эти поверхности являются не только наиболее распространенными, но и наиболее простыми по своему образованию. Наряду с такими поверхностями в технике применяются поверхности более сложного образования: цилиндроид, коноид, наклонный геликоид и винтовой цилиндр круглого нормального сечения. Для образования этих поверхностей в качестве направляющих часто используются винтовые линии. Поверхности, образованные с помощью винтовых линий, называют винтовыми поверхностями. Цилиндроид. Поверхность цилиндроида образуется при перемещении прямой образующей линии 1 по двум кривым направляющим тип (рис. 298) при условии, что эта образующая все время остается параллельной некоторой заданной плоскости параллелизма σ (плоскость направления). Из комплексного чертежа видно, что образующие l, l1, l2, l3 параллельны плоскости параллелизма σ, так как их горизонтальные проекции l1, l2 и др. параллельны горизонтальной проекции χ горизонтально-проецирующей плоскости о. Цилиндроид подобного образования используется при конструировании и изготовлении отвалов плугов, в кузовостроении и при устройстве сводов. Несколько иначе, с использованием винтовой линии, образуется поверхность винтового цилиндроида, применяющаяся при конструировании и изготовлении режущих инструментов (рис. 299).
Рис. 298. Цилиндроид
Рис. 299. Пример винтового цилиндроида — сверло по дереву Коноид. Поверхность коноида образуется при перемещении образующей по двум направляющим, из которых одна — кривая, другая — прямая линия; образующая перемещается, оставаясь все время параллельной заданной плоскости параллелизма. Для образования поверхности винтового коноида строят цилиндрическую винтовую линию 09 (рис. 300, а) и заставляют образующую перемещаться по этой винтовой и по ее оси так, чтобы она все время была параллельна горизонтальной плоскости (плоскости параллелизма). Если винтовой коноид рассечь цилиндром, имеющим с коноидом общую ось и меньший диаметр, то при пересечении получится винтовая линия того же шага. Часть поверхности, заключенной между винтовыми линиями, называется кольцевым коноидом (горизонтальная проекция имеет вид кольца). Любое сечение коноида плоскостью А—А, параллельной плоскости параллелизма, является прямой линией (прямая 10—11). Винтовой коноид применяют в прямоугольных резьбах (рис. 300, б). Для изображения винта строят ряд винтовых, линий различных диаметров (1 и 2 для большого диаметра d; 3 и 4 для малого — d1). На чертеже построен разрез винта горизонтальной плоскостью А—А. Изображенный винт — однозаходный. Винтовой коноид применяют также в транспортирующих устройствах (шнеки), при устройстве винтовых лестниц, въездов в многоэтажные гаражи (пандусы) и т. д.
Рис. 300. Винтовой коноид и его применение Винтовые поверхности Поверхность, образованная винтовым движением прямой линии, называется линейчатой винтовой поверхностью - геликоидом (винтовое движение характеризуется вращением вокруг некоторой оси i и поступательным перемещением, параллельным этой оси). а. Прямой геликоид Рис.
2.3.40 Если
в качестве кривой направляющей коноида
взять цилиндрическую винтовую линию,
в качестве прямой направляющей - ось
винтовой линии, а за плоскость
параллелизма - плоскость, перпендикулярную
оси винтовой линии, то поверхность,
образованная при этих условиях,
называется винтовым коноидом или
прямым геликоидом (рис. 2.3.40). Очевидно,
что образующая прямая прямого геликоида
пересекает ось под прямым углом.
На
рис. 2.3.41 показана кинематика построения
прямого открытого геликоида. Видно,
как образующая прямая перемещается
параллельно плоскости основания
(плоскость параллелизма) и в каждый
момент пересекает две направляющие:
винтовую линию и прямую - ось этой
винтовой линии.
На рис. 2.3.42 приведен пример прямого открытого геликоида, имеющего конечную толщину поверхности.
б. Наклонный геликоид Наклонным
геликоидом называется поверхность,
образованная движением прямой линии,
cкользящей по двум направляющим (одна
из них цилиндрическая винтовая линия,
а вторая - ось винтовой линии) и
сохраняющей во всех положениях
постоянный угол
Направляющий
конус соосен с винтовой поверхностью,
его образующие наклонены под углом Рассмотренные винтовые поверхности, так же как и поверхности вращения, обладают свойством сдвигаемости, т. е. поверхность может перемешаться вдоль самой себя без каких-либо деформаций. Это свойство поверхности широко используется в технике при создании винтовых пар (винт-гайка). На рис. 2.3.44 показан наклонный закрытый геликоид
|
|


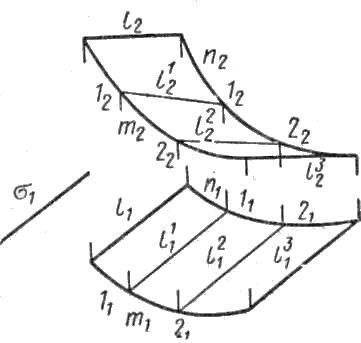



 Рис.
2.3.41
Рис.
2.3.41
