2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента

Основные вычисления в методе исключений Гаусса выполняются по формулам (2.7) – (2.9). Граф процесса вычисления коэффициентов по формуле (2.8) представлен на рисунке 2.1. Этот граф позволяет проследить накопление погрешностей в процессе вычислений по методу Гаусса.

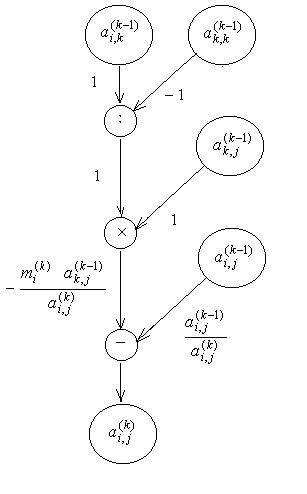
Рисунок 2.1 – Граф процесса вычисления коэффициента

Обозначим относительную погрешность, содержащуюся в коэффициенте , – относительные погрешности округления соответственно при делении, умножении и вычитании. Тогда для относительной погрешности коэффициента можно получить выражение

.

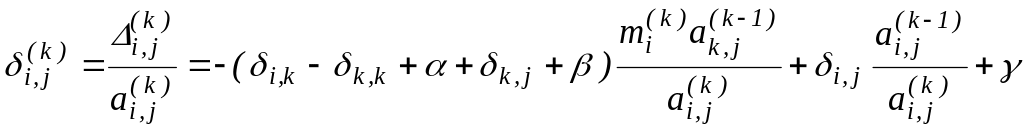Отсюда получаем формулу для оценки абсолютной погрешности :

.

Если предположить, что погрешности , не превышают некоторой величины , то получим следующую формулу для оценки погрешности:

.

Из последнего выражения видно, что погрешность вычисления коэффициента в основном определяется первым слагаемым правой части и уменьшается с уменьшением . Чтобы было по возможности меньшим, необходимо чтобы было по возможности большим (см. формулу (2.7)). Поэтому перед выполнением шага исключения каждой переменной желательно переставить уравнения системы так, чтобы

, ,

потому что тогда

.

Если в методе Гаусса выполняется такая перестановка, то метод называется методом Гаусса с выбором главного элемента. Этот метод имеет меньшую погрешность при определении решения СЛАУ.

2.4 Обращение матрицы

Как известно, матрица называется обратной матрице , если выполняется соотношение

, (2.10)

где – единичная матрица. Обозначим , , , где – символ Кронекера,

Тогда соотношение (2.10) можно записать так:

, . (2.11)

Из этого выражения видно, что если рассматривать -й столбец обратной матрицы как вектор, то он является решением системы линейных алгебраических уравнений (2.11) с матрицей и вектором правой части, все элементы которого равны нулю, кроме -го, который равен 1. Таким образом, элементы обратной матрицы могут быть получены решением системы линейных алгебраических уравнений. Для обращения матрицы необходимо решить систем линейных уравнений с одинаковой матрицей и разными правыми частями. Приведение матрицы к треугольному виду по формулам (2.8), (2.9) делается при этом только один раз. В дальнейшем необходимо формировать новую правую часть, преобразовывать ее при помощи чисел (2.7) по формуле (2.9) и для каждой правой части выполнять обратный ход. Понятно, что преобразующие числа , , необходимо сохранять по мере их получения на этапе прямого хода. Видно, что эти числа образуют нижнюю треугольную матрицу, совпадающую по размерам с матрицей исключаемых коэффициентов системы. Поэтому число можно поместить на место элемента .

Для обращения матрицы этим методом требуется примерно ячеек оперативной памяти и примерно арифметических операций.

Описанный прием вычислений можно применить при решении систем уравнений с одной и той же матрицей и различными правыми частями. В этом случае выгодно привести матрицу к треугольному виду только однажды, используя сохраненные числа во всех последующих вычислениях.