6.4.Постановка граничных условий и стабилизация макросостояния молекулярно-динамической системы

В настоящем пособии мы рассматриваем только моделирование кристал­лов с нулевыми граничными условиями, т.е. – кристаллитов с конечным числом частиц в вакууме. Применение таких граничных условий в идеале не требует для расчёта сил, скоростей и перемещений ионов никаких других уравнений, кроме соотношений -. Однако, накопление вычислитель­ных погрешностей приводит к нарушениям законов сохранения импульса, момента импульса и энергии, что может приводить к появлению движения и вращения кристалла как целого, а также к росту его температуры. Для исключения этих эффектов можно использовать следующие методы.

6.4.1.Компенсация импульса и момента импульса

Импульс модельного кристалла из N частиц даётся формулой

,

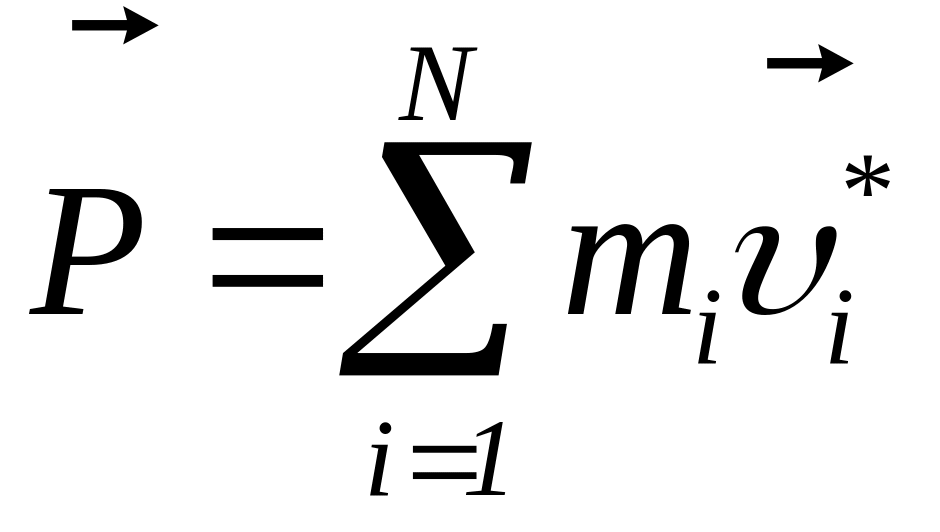где m_i – массы частиц,  - их скорости до компенсации импульса. Скорость центра инерции кристалла связана с импульсом соотношением

.

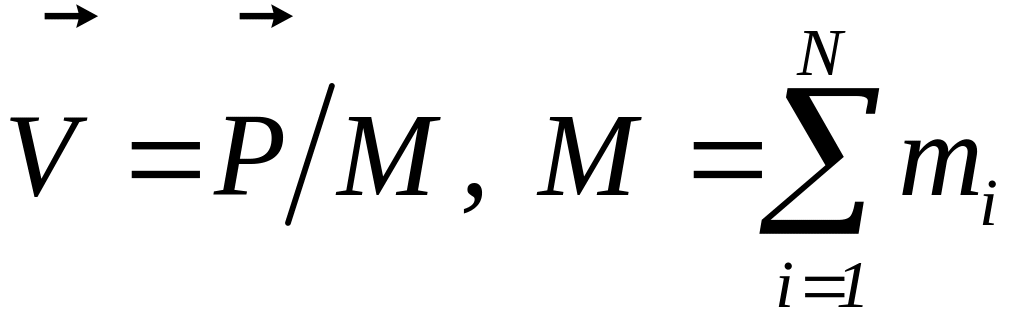Вычитание этой скорости из скоростей всех частиц останавливает собственное движение кристалла:

.

Предположим, что кристалл только вращается как твердое тело вокруг какой-нибудь оси, и больше частицы никуда не движутся (для упрощения выражений). Это вращение харак­теризуется постоянной угловой скоростью , связанной со скоростями частиц соотноше­нием

.

Здесь  - скорости и координаты i-ой частицы. Момент импульса этого кристалла рас­считывается по формуле

,

где N – количество частиц. Двойное векторное произведение можно преобразовать по формуле

,

тогда получится, что

.

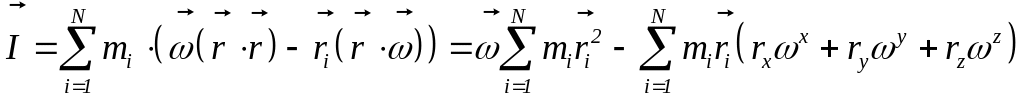Это векторное уравнение эквивалентно системе из трех уравнений для компонент векто­ров и :

.

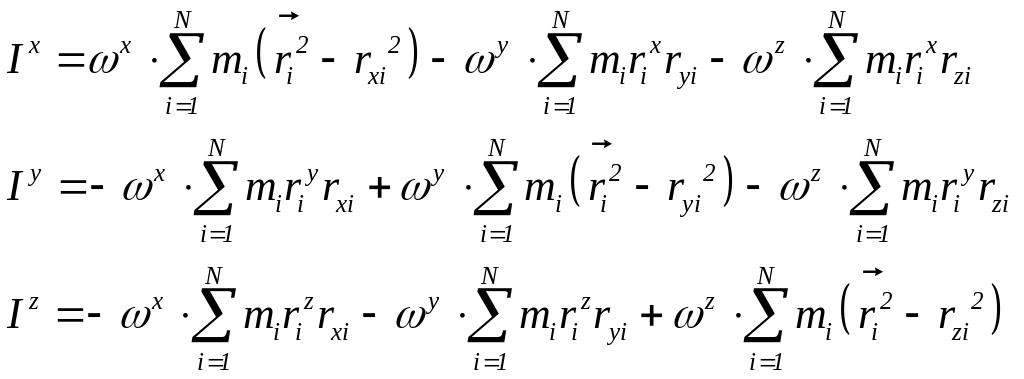Значения компонент векторов с верхними и нижними индексами одинаковы – положение индексов указывает на ко- и контравариантность векторов. Отметим также, что слагаемые вида

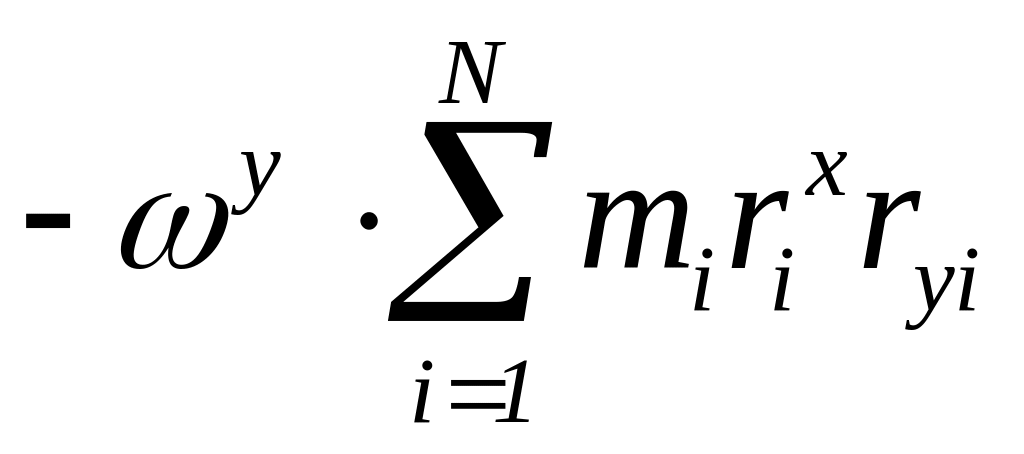
для симметричного относительно оси вращения кристалла равны нулю, так что и для реальных кристаллов должны быть близки к нулю.

Таким образом, если для кристалла с произвольными скоростями частиц рассчитан мо­мент импульса , то может быть, решением записанной системы уравнений, получена соответствующая угловая скорость . Если теперь получить новые скорости частиц по формуле

,

то момент импульса кристалла станет равным нулю. При этом изменение самого импуль­са будет иметь вид

,

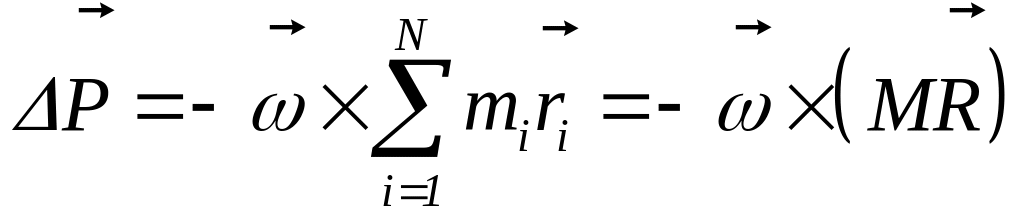где M – масса кристалла,  - радиус-вектор центра инерции. Очевидно, что если отсчи­тывать координаты от центра инерции, то , и импульс не изменится. Кроме того, перед остановкой вращения кристалла нужно обнулить суммарный импульс, тогда ось вращения обязательно будет проходить через центр инерции, что подразумевается в формуле .

6.4.2.Стабилизация температуры

Стабилизация температуры моделируемой системы в принципе может быть необходима по двум причинам:

 образование дефектов кристаллической решётки, суперионный переход и плавление требуют энергии, так что в изолированной системе происходит повышение потенциальной энергии за счёт понижения температуры; поэтому, для моделирования кристаллов с постоянной температурой необходим алгоритм стабилизации температуры, моделирующий взаимодействие с термостатом;

 опыт показывает, что накопление вычислительной погрешности приводит к медленному, но существенному при больших временах моделирования разогреву кристаллитов; для предотвращения разогрева тоже необходима стабилизация температуры.

Идея стабилизации состоит в том, что в уравнения движения изолированной системы добавляется дополнительное слагаемое, понижающее скорости частиц в случае, если температура системы превосходит заданную и увеличивающее скорости в противоположном случае.

Модификация скоростей производится умножением импульсов на коэффициент p_/Q, одинаковый для всех частиц , так что она не приводит к возникновению движения или вращения системы как целого.

Применение стабилизирующей температуру поправки в форме - было предложено Рябовым. Из его работ следует, что в форме - уравнения движения системы соответствуют гамильтониану, совпадающему с выражением для энтальпии H, так что они физически корректно описывают кристаллиты при нулевом (пренебрежимо малом) внешнем давлении и постоянной температуре.

Таким образом, для термостатирования системы с нулевыми граничными условиями можно использовать следующие уравнения движения молекул:

;

;

.

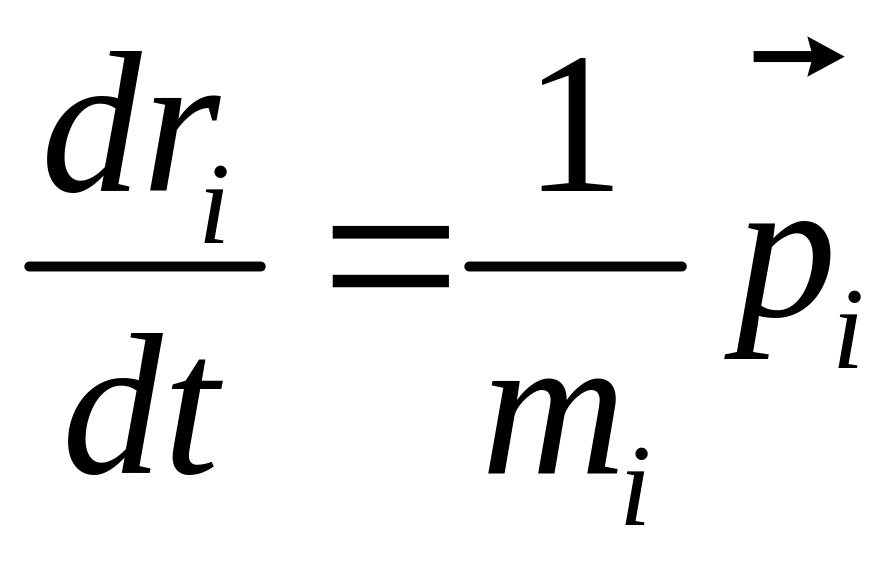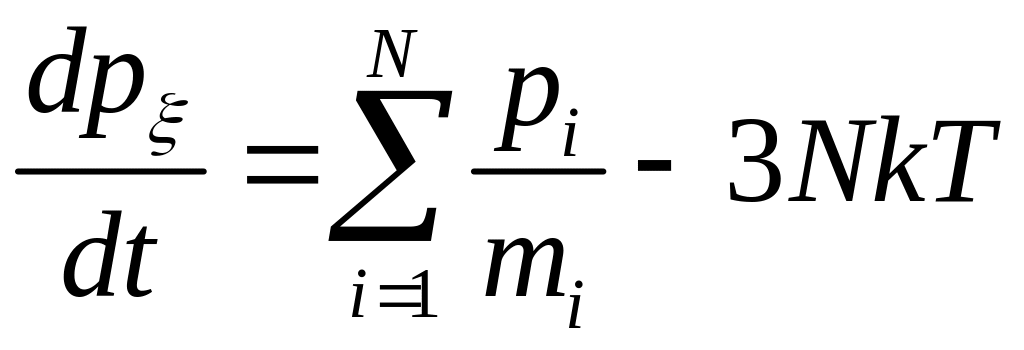Здесь N – количество частиц в системе; T – требуемая температура; p_ - дополнительная переменная размерности Джс, связанная с термостатом, Q – величина размерности Джс², задающая частоту колебаний температуры; индекс  не имеет самостоятельного значения, он только показывает, что p_ - переменная, относящаяся к стабилизации температуры.

В начале моделирования можно принять, что p_ = 0. На последующих шагах моделирования эта величина изменяется по формуле

.

Значение константы Q в принципе произвольно, однако этим значением определяются период и амплитуда колебаний задаваемой температуры. Оценить необходимое значение Q можно из следующих соображений.

Из-за слагаемого, соответствующего термостату, к скоростям частиц добав­ляется поправка

.

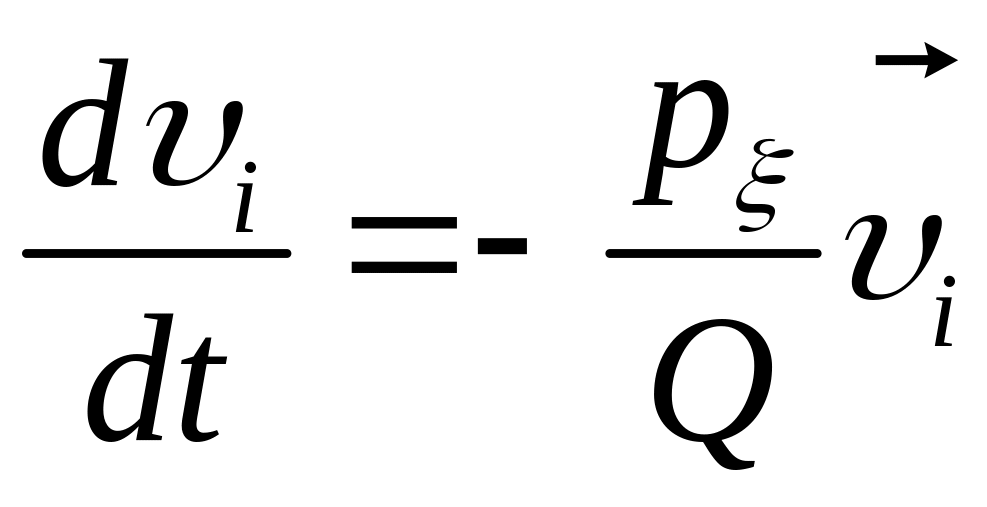Если домножить обе части уравнения на и просуммировать по всем i, то получится, что

,

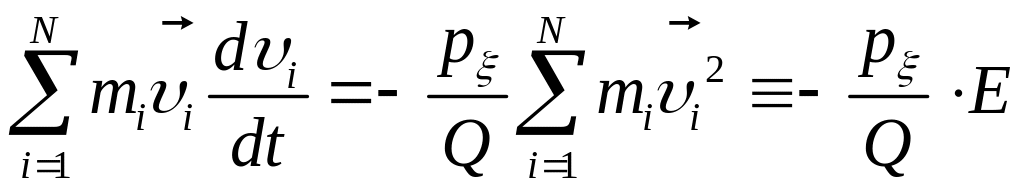где E – удвоенная кинетическая энергия системы. Её требуемое значение как раз и равно 3NkT. Учтём то, что

и то, что, в соответствии с формулами и ,

.

Таким образом, временная зависимость отклонения величины E от 3NkT даётся уравнением

.

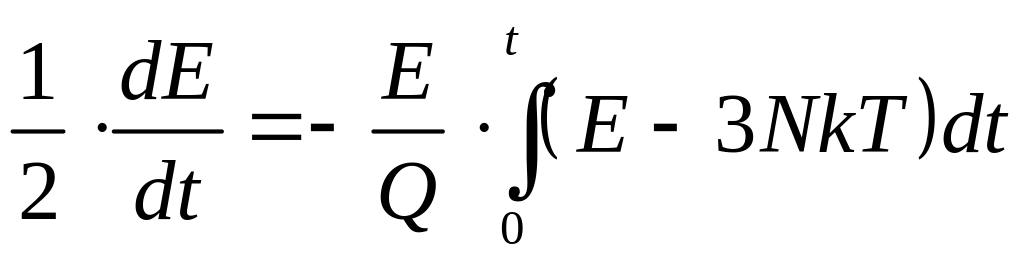Можно переписать уравнение в приближённой форме, считая, что E  3NkT; это верно, если температура колеблется не сильно. Кроме того, вводим новую переменную

,

причём

.

Теперь, дифференцируя обе части уравнения по времени, в приближении E  3NkT получаем

.

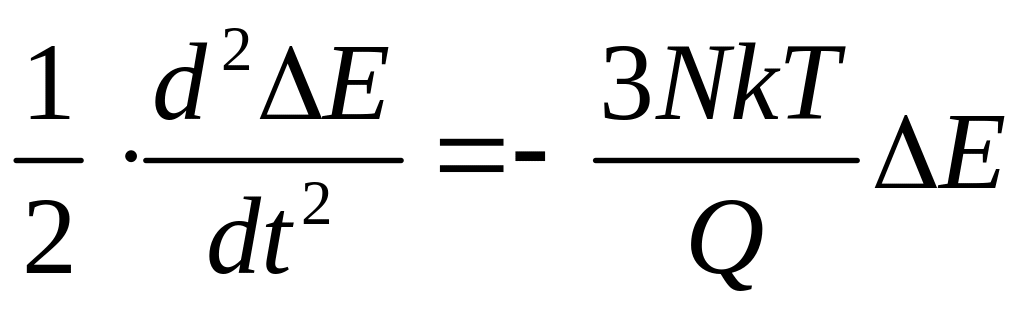Это – уравнение гармонических колебаний с циклической частотой

,

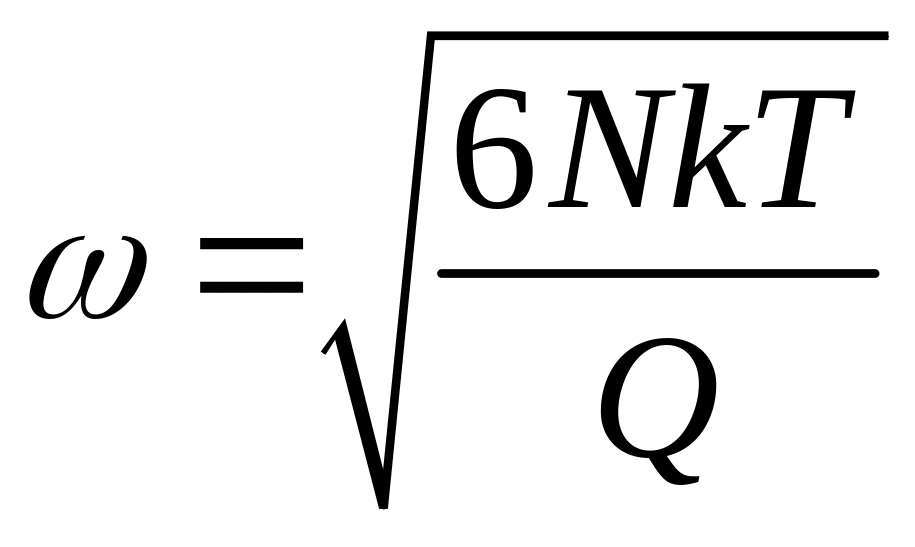откуда

,

где  - период колебаний.

Выражение позволяет выбирать значение Q, исходя из требований, предъявляемых к периоду колебаний. Например так, чтобы период колебаний был существенно меньшим, чем время моделирования.