Обобщенный ряд Фурье

Произвольный сигнал s(t) может быть представлен рядом где C_n – коэффициенты, зависящие от вида s(t), а u_n – n-я функция выбранного базиса , причем базисные функции на интервале ортогональности должны обладать свойствами:

а) ортогональности , при , [a,b] – интервал ортогональности.

б) конечности энергии: 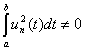. Величина этой энергии называется квадратом нормы:

.

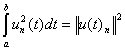Коэффициенты обобщенного ряда Фурье определяются по формуле:

.

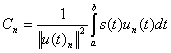Если набор базисных функций содержит комплексные функции, то свойства отображаются таким образом: - для ; здесь - функция, комплексно сопряженная u_k(t); , а комплексные коэффициенты ряда определяются соотношением:

.

Тригонометрический ряд Фурье

Пусть имеется периодический сигнал с периодом Т: т.е. Для тригонометрического ряда Фурье набор базисных функций имеет вид:

где - частота первой гармоники;

Частоты или - частоты высших гармонических составляющих.

Интервал ортогональности в этом случае равен Т. Тригонометрические функции кратных аргументов ортогональны друг другу. Квадрат нормы базисной функции u₀(t)=1 равен:

;

квадрат нормы для базисных функций равен:

;

квадрат нормы для функций равен

.

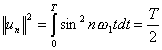Таким образом, коэффициенты ряда определяются как:

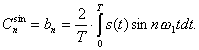
Тригонометрический ряд Фурье будет иметь вид:

.

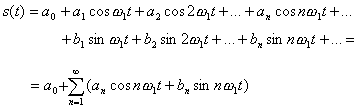Преобразуем каждую пару с одинаковыми частотами:

.

Действительно: . Таким образом: . Величину a₀ можно выразить через общую формулу для при n=0, тогда .

Обозначив , получаем известную форму записи тригонометрического ряда Фурье:

.

Для четных функций s(t) все нечетные члены ряда равны 0, т.е. b_n=0, следовательно .

Для нечетных функций, все четные члены ряда равны 0, т. е. все a_n, в том числе и a₀ равны 0, следовательно .

Временная интерпретация тригонометрического ряда Фурье показана на рис. 1.

Складывая в каждый момент времени мгновенные значения всех гармоник, получаем мгновенное значение самого сигнала в этот момент времени.

Нахождение частот, амплитуд и фаз составляющих сигнала называется спектральным анализом. Получение сигнала по заданным коэффициентам , фазам , и частотам называется синтезом сигналов. Складывая ограниченное число гармоник, получаем сигнал, отличный от того, для которого рассчитывались амплитуды и фазы гармоник.

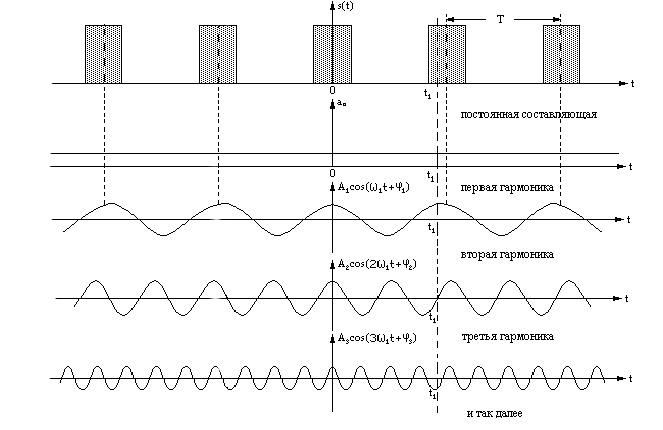
Рис. 1

Действительный частотный спектр сигнала

 

Совокупность частот образует частотный спектр сигнала (частотный состав), график в координатах (частота, амплитуда) называется амплитудно-частотным спектром сигнала (АЧС), а (частота, фаза) фазочастотным спектром сигнала (ФЧС). Пример АЧС и ФЧС показан на рис. 2.

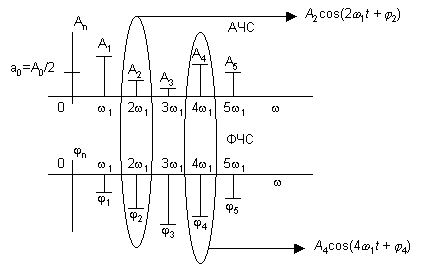
Рис.2

Каждая гармоническая составляющая отображается отрезками амплитуды и фазы на соответствующей частоте. Любая спектральная составляющая сигнала в соответствии со спектром может быть записана в тригонометрической форме. На рис.2. отмечены и записаны мгновенные значения для второй и четвертой гармоник.

Действительный частотный спектр (в дальнейшем будем опускать слово «частотный») позволяет наглядно оценить частотные свойства сигнала: полосу частот, занимаемую сигналом, если спектр ограничен по частоте («финитный спектр»), полосу частот, в которой сосредоточена основная энергия сигнала.