4. Проверка плана на оптимальность

Теорема 8.1. Если для некоторого опорного плана ТЗ существуют числа (потенциалы поставщиков) и числа (потенциалы потребителей), такие что (8.1) для (клетка заполнена) и (8.2) для (клетка пуста) , то план является оптимальным.

Для заполненных клеток составляется система, которая содержит n+m–1 уравнение и n+m неизвестных. Поэтому полагается, что , а затем находятся остальные переменные.

Для свободных клеток определяются числа . Если , то условия теоремы выполнены, план оптимален. Если же , то план не оптимален, и его следует улучшить.

Проверим на оптимальность план, полученный по методу минимального элемента:

		120	50	190	110
	160
	140
	170

Для составим систему уравнений:

,

, Пусть , =0,

, = -4, =0,

, =-2 , =1,

, =4.

.

Для подсчитаем значения выражений:

,

,

,

,

,

.

Так как получена положительная разность , то план не оптимален.

5. Цикл пересчета

Определение 8.2. Цикл пересчета – замкнутая ломаная с вершинами в заполненных клетках и звеньями, расположенными вдоль строк и столбцов матрицы перевозок, при этом одна вершина находится в заполняемой клетке.

Цикл пересчета позволяет таким образом перераспределить поставки, чтобы не нарушить баланса перевозимого и поставляемого груза. Для любой свободной клетки можно построить единственный цикл пересчета.

Примеры. На рисунке 8.1 изображены возможные варианты циклов пересчета:

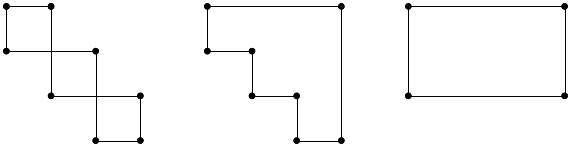
Рис. 8.1

Алгоритм улучшения опорного плана:

1) Среди всех выбирают максимальное.

2) Для соответствующей клетки строят цикл пересчета.

3) Помечают вершины цикла пересчета последовательно знаками «+» и «–», начиная с «+» в исходной клетке.

4) Среди чисел, стоящих в клетках, помеченных «–» определяют минимальное.

5) К значениям, стоящим в «+» клетках, прибавляют это минимальное число, а из значений, стоящих в «–» клетках, это число вычитают.

6) Проверяют полученный план на оптимальность.

Продолжим решение, сформулированной ранее задачи. Поскольку , то для соответствующей клетки необходимо построить цикл пересчета:

	120	50	190	110
160
140
170

Строя цикл пересчета по указанному алгоритму, получаем новый план перевозок, представленный в следующей транспортной таблице:

		120	50	190	110
	160
	140
	170

Новый план невырожденный. Проверим его на оптимальность.

Для :

, Пусть , =-2,

, = -6, =0,

, =-2, =1,

, =2.

,

.

Для :

,

,

,

,

,

.

Так как , то план не оптимален и для соответствующей клетки необходимо построить цикл пересчета:

	120	50	190	110
160
140
170

Получаем новый план перевозок, представленный в следующей транспортной таблице:

		120	50	190	110
	160
	140		20
	170

Проверим план на оптимальность.

Для :

, Пусть , =-1,

, = -5, =0,

, = -2, =1,

, =2.

,

.

Для :

,

,

,

,

,

.

Все разности не положительны, следовательно, получен оптимальный план.

Оптимальные затраты Полученное значение совпадает со значением целевой функции опорного плана решения задачи по методу Фогеля. Это говорит о том, что в данном случае опорный план, построенный по методу Фогеля, приводит к получению оптимального плана решения ТЗ быстрее, чем по методу минимального элемента.

Ответ: ,
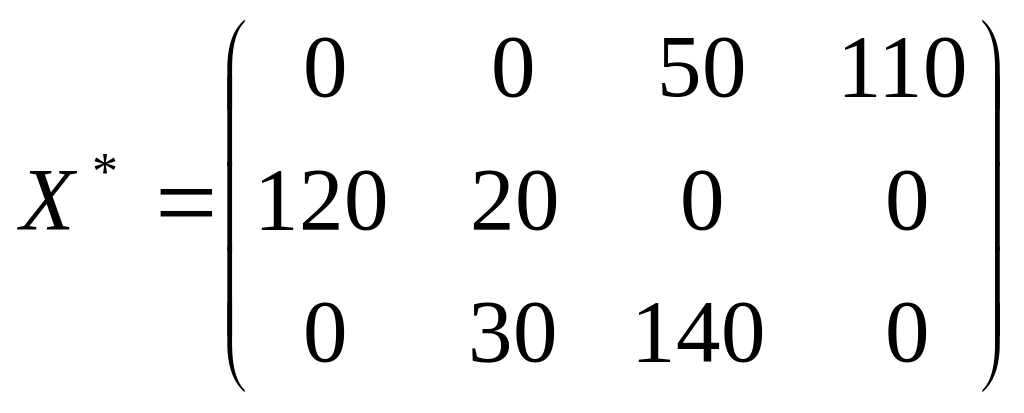