Тема 7. Матричные статистические игры

План лекции:

1. Понятие статистической игры

2. Критерии выбора оптимальной стратегии при решении

статистической игры

3. Кооперативные игры

1. Понятие статистической игры

Статистическая игра является специфическим видом матричных игр. В них один из игроков является нейтральным, то есть не ведет активного противодействия другому участнику игры, но хранит втайне свою стратегию. Обычно такого игрока называют «природой», окружающей средой или обстановкой. «Природа» коварна, но не злонамеренна, она не стремится использовать в своих интересах ошибки противника или информацию о его стратегии. Игрока с природой часто называют статистиком.

Определение 7.1. Игры, в которых один участник – «природа», а другой – лицо, принимающее решение, или, в которых один из игроков действует неосознанно, а в соответствии с определенными законами, называют играми с природой или статистическими играми.

Выбирая свою стратегию, статистик не в полной мере осведомлен о состоянии природы (ее стратегии, например, условия погоды, спрос на определенную продукцию, объем перевозок, некоторое сочетание производственных факторов и т.д.).

Неизбежной платой за попытку принятия решения в условиях неполной информации о состоянии природы является возможность принятия статистиком ошибочных (не оптимальных) решений. В подобной ситуации разумной является такая стратегия статистика, при которой хотя и не исключена возможность принятия не самых лучших решений, но в определенном смысле сводятся к минимуму, связанные с этим нежелательные решения.

Теория статистических игр называется теорией статистических решений.

Условия игры задаются в виде матрицы , в которой строки соответствуют стратегиям человека, а столбцы – возможным состояниям «природы». Элемент равен выигрышу статистика, если он использует i-тую стратегию при j-том состоянии природы.

Также рассматривается матрица рисков , которая зачастую дает наиболее наглядную картину неопределенной ситуации, чем матрица выигрышей. Элемент равен разности между выигрышем, который получил бы человек, если бы он знал состояние природы, и выигрышем, который он получит в тех же условиях, применяя i-тую стратегию, то есть

.

2. Критерии выбора оптимальной стратегии при решении статистической игры

Задача. Планируется проведение концертно-развлекательного мероприятия на открытой площадке в заранее неизвестных метеорологических условиях. Можно выделить 4 варианта этих условий: . Согласно архивным материалам метеосводок за много лет вероятности этих вариантов равны соответственно величинам . Возможные варианты программ мероприятия в различных метеоусловиях дают различный доход, значения которого приведены в платежной матрице:

.

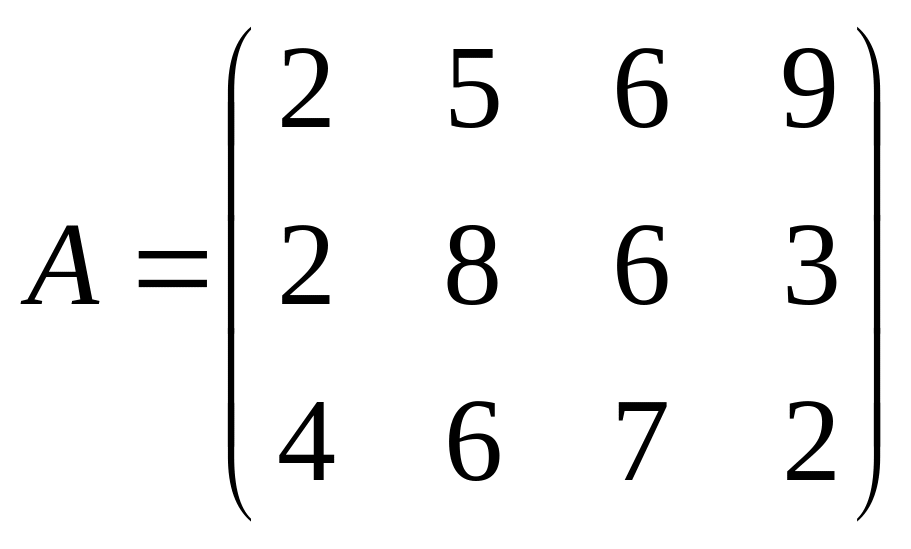Обосновать рекомендации устроителям мероприятия: а) при известном распределении вероятностей метеорологических условий; б) в случае неизвестных вероятностей метеорологических условий (при использовании критерия Гурвица положить ).

Если вероятности состояний природы известны, то при решении задач теории статистических решений пользуются критерием Байеса.

Критерий Байеса. Пусть известны вероятности возможных состояний природы . В качестве оптимальной стратегии статистика применяется чистая стратегия , при которой максимизируется средний выигрыш статистика.

.

Определим оптимальную стратегию проведения мероприятия по критерию Байеса:

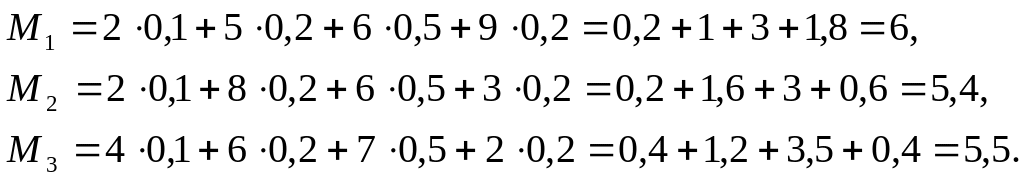
Следовательно, .

Таким образом, оптимальной следует считать первую стратегию статистика А₁.

Если распределение вероятностей p_j состояний природы B_j неизвестно, то используются следующие критерии.

Критерий «недостаточного основания Лапласа». В условиях неизвестного распределения вероятностей состояний природы все состояния полагаются равновероятными . Оптимальной считается стратегия, обеспечивающая максимум среднего выигрыша:

.

Определим оптимальную стратегию проведения мероприятия по критерию Лапласа с учетом :

Следовательно, .

Итак, оптимальной следует считать первую стратегию статистика А₁.

Максиминный критерий Вальда. В качестве оптимальной выбирается стратегия статистика, при которой минимальный выигрыш максимален, то есть статистику гарантируется выигрыш не меньше, чем нижняя цена игры с природой:

.

Найдем оптимальное решение статистической игры, используя критерий Вальда:

.

Следовательно, в качестве оптимальной следует считать или стратегию статистика.

Критерий минимального риска Сэвиджа. В условиях неопределенности в качестве оптимальной выбирается та стратегия, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск минимален):

.

Найдем оптимальное решение статистической игры, используя критерий Сэвиджа. Составим матрицу рисков:

.

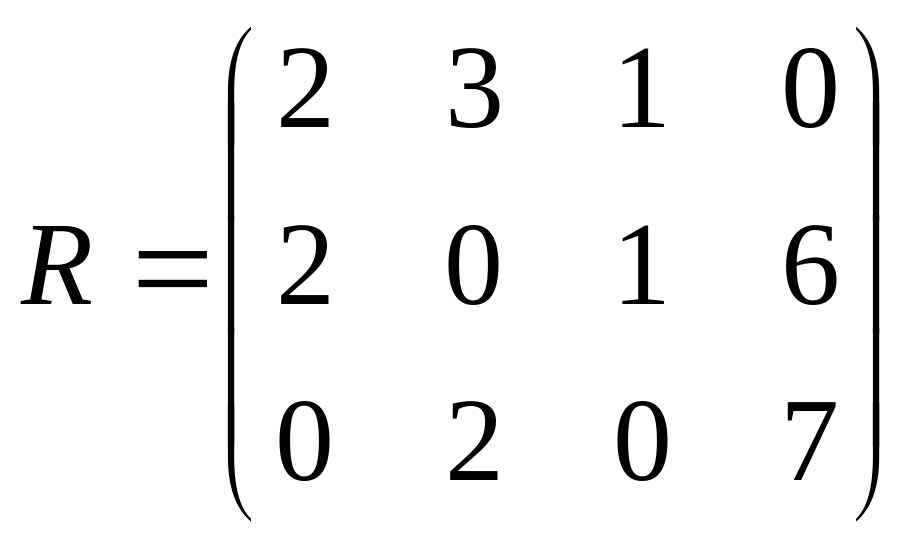Найдем величину .

Таким образом, оптимальной следует считать первую стратегию статистика А₁.

Критерии Вальда и Сэвиджа ориентируют статистика на самые неблагоприятные состояния природы, то есть эти критерии выражают пессимистическую оценку ситуации. При использовании критерия Вальда из худших обстоятельств выбирается лучшее, а при использовании критерия Сэвиджа – из наивысших рисков выбирается меньший.

Критерий пессимизма – оптимизма Гурвица. В качестве оптимальной стратегии статистика выбирается та, для которой выполняется соотношение.

где .

При получаем критерий крайнего оптимизма, а при – критерий пессимизма Вальда. Если , то получаем нечто среднее. При желании подстраховаться в данной ситуации принимают близким к единице. В общем случае число выбирают исходя из опыта или субъективных соображений.

Найдем оптимальное решение статистической игры, используя критерий Гурвица. По условию . Тогда

.

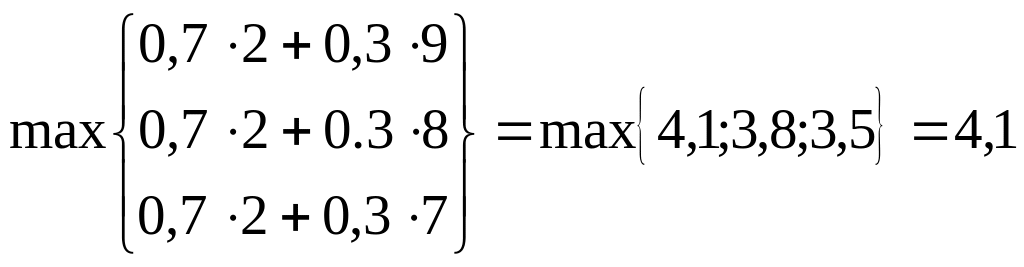Следовательно, оптимальной следует считать первую стратегию статистика А₁.

Перебирая результаты определения оптимальной стратегии по различным критериям, можно сделать вывод о том, что предпочтение следует отдать стратегии А₁.

Решение статистической игры по рассмотренным критериям позволяет более обоснованно принимать ту стратегию, которая гарантирует статистику больший выигрыш по сравнению с выигрышем, принимаемым статистиком инициативно или исходя из опыта.