3.3. Теоремы о парах

Докажем три теоремы, с помощью которых становятся возможными эквивалентные преобразования пар. При всех рассмотрениях следует помнить, что они относятся к парам, действующим на какое-либо одно твердое тело.

Т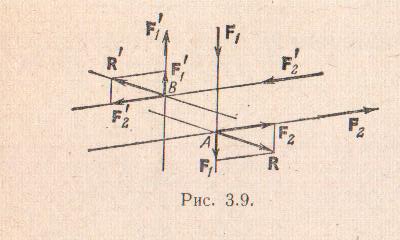 еорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар.

Для доказательства этой теоремы рассмотрим две пары (F₁, F'₁) и (F₂, F'₂) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим

R=F₁+F₂ и R'=F'₁+F'₂,

но F₁=-F'₁ и F₂=-F'₂.

Следовательно, R=- R', т.е. силы R и R' образуют пару. Найдем момент этой пары, воспользовавшись формулой (3.13):

М=М(R, R')=ВА× R=ВА×(F₁+F₂)=ВА×F₁+ВА×F₂. (3.14)

При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пар не меняются, следовательно, не меняется и момент пары. Значит,

ВА×F₁=М(F₁, F'₁)=М₁, ВА×F₂= М(F₂, F'₂)=М₂

и формула (3.14) примет вид

М=М₁+М₂, (3.15)

что и доказывает справедливость сформулированной выше теоремы.

Сделаем два замечания к этой теореме.

1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае, но для ее доказательства следует воспользоваться правилом сложения параллельных сил.

2. После сложения может получиться, что М(R, R')=0; на основании сделанного ранее замечания из этого следует, что совокупность двух пар (F₁, F'₁, F₂, F'₂)=0.

Теорема 2. Две пары, имеющие геометрически равные моменты, эквивалентны.

Пусть на тело в плоскости I действует пара (F₁, F'₁) с моментом М₁. Покажем, что эту пару можно заменить другой с парой (F₂, F'₂), расположенной в плоскости II, если только ее момент М₂ равен М₁ (согласно определению (см. 1.1) это и будет означать, что пары (F₁, F'₁) и (F₂, F'₂) эквивалентны). Прежде всего заметим, что плоскости I и II должны быть параллельны, в частности они могут совпадать. Действительно, из параллельности моментов М₁ и М₂ (в нашем случае М₁= М₂) следует, что плоскости действия пар, перпендикулярные моментам, также параллельны.

Введем в рассмотрение новую пару (F₃, F'₃) и приложим ее вместе с парой (F₂, F'₂) к телу, расположив обе пары в плоскости II. Для этого, согласно аксиоме 2 нужно подобрать пару (F₃, F'₃) с моментом М₃ так, чтобы приложенная система сил (F₂, F'₂, F₃, F'₃) была уравновешена. Это можно сделать, например, следующим образом: положим F₃=-F'₁ и F'₃=-F₁ и совместим точки приложения этих сил с проекциями А₁ и В₁ точек А и В на плоскость II. В соответствии с построением будем иметь: М₃= -М₁ или, учитывая, что М₁= М₂,

М₂+М₃=0.

Принимая во внимание второе замечание к предыдущей теореме, получим (F₂, F'₂, F₃, F'₃)=0. Таким образом, пары (F₂, F'₂) и (F₃, F'₃) взаимно уравновешены и присоединение их к телу не нарушает его состояния (аксиома 2), так, что

(F₁, F'₁)= (F₁, F'₁, F₂, F'₂, F₃, F'₃). (3.16)

С другой стороны, силы F₁ и F₃, а также F'₁ и F'₃ можно сложить по правилу сложения параллельных сил, направленных в одну сторону. По модулю все эти силы равны друг другу, поэтому их равнодействующие R и R' должны быть приложены в точке пересечения диагоналей прямоугольника АВВ₁А₁; кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю. Итак,

(F₁, F'₁, F₃, F'₃)=(R, R')=0.

Теперь мы можем записать

(F₁, F'₁, F₂, F'₂, F₃, F'₃)=(F₃, F'₃). (3.17)

Сравнивая соотношения (3.16) и (3.17), получим (F₁, F'₁)=(F₂, F'₂), что и требовалось доказать.

Из этой теоремы следует, что пару сил можно перемещать в плоскости ее действия, переносить в параллельную плоскость; наконец, в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁= F₂h₂).

В дальнейшем мы будем широко пользоваться такими эквивалентными преобразованиями пары.

Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар.

Пусть пары (F₁, F'₁) и (F₂, F'₂) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ, расположенному на линии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q₁, Q'₁) и (Q₂, Q'₂). При этом должны выполняться равенства

М₁=М(Q₁, Q'₁)=М(F₁, F'₁) и М₂=М(Q₂, Q'₂)=М(F₂, F'₂).

Сложим по аксиоме 3 силы, приложенные в точках А и В соответственно. Тогда получим R=Q₁+Q₂ и R'= Q'₁+Q'₂. Учитывая, что Q'₁=-Q₁ и Q'₂=-Q₂, получим R=-R'. Таким образом , мы доказали, что система двух пар эквивалентна одной паре (R, R').

Н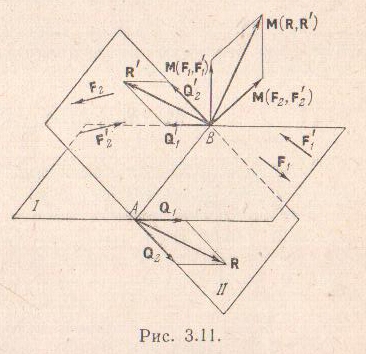 айдем момент М этой пары. На основании формулы (3.13) имеем

М(R, R')=ВА×(Q₁+Q₂)=ВА×Q₁+ВА×Q₂=

=М(Q₁, Q'₁)+М(Q₂, Q'₂)=М(F₁, F'₁)+М(F₂, F'₂)

или

М=М₁+М₂,

т.е. теорема доказана.

Заметим, что полученный результат справедлив и для пар, лежащих в параллельных плоскостях. По теореме 2 такие пары можно привести к одной плоскости, а по теореме 1 их можно заменить одной парой, момент которой равен сумме моментов составляющих пар.

Доказанные выше теоремы о парах позволяют сделать важный вывод: момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. В самом деле, мы уже доказали, что если две пары имеют одинаковые моменты (следовательно, лежат в одной плоскости или в параллельных плоскостях), то они друг другу эквивалентны (теорема 2). С другой стороны, две пары, лежащие в пересекающихся плоскостях, не могут быть эквивалентны, ибо это означало бы, что одна из них и пара, противоположная другой, эквивалентны нулю, что невозможно, так как сумма моментов таких пар отлична от нуля.

Таким образом, введенное понятие момента пары чрезвычайно полезно, так как оно полностью отражает механическое действие пары на тело. В этом смысле можно сказать, что момент исчерпывающим образом представляет действие пары на твердое тело.

Для деформируемых тел изложенная выше теория пар неприменима. Две противоположные пары, действующие, например, по торцам стержня, с точки зрения статики твердого тела эквивалентны нулю. Между тем их действие на деформируемый стержень вызывает его кручение, и тем большее, чем больше модули моментов.

Перейдем к решению первой и второй задач статики, когда на тело действуют только пары сил.