Расчетно-графическая работа № 2.

Расчёт стержней и стержневых систем на растяжение сжатие.

Задача № 3

Расчёт статически неопределимой стержневой системы

Дано: стержневая система состоит из абсолютно жёсткого бруса, который опирается на шарнирно неподвижную опору, и двух деформируемых стержней, шарнирно соединённых с брусом и с основанием (рис. 3.1).

Материал - сталь Ст.3, Е=2×10⁵ МПа, [σ]=160 МПа, α=120×10^-7 ˚С^-1; материал - медь, E=1×10⁵ МПа, [σ]=120 МПа, α=167×10^-7 ˚С^-1; a = 1.5 м. b = 2 м, c = 1.3 м, l = 2 м, ₁=60º, ₂=45º, A₁=0.5A₂, F=90 кН, q=40 кН, δ = 0.12 мм, Δt = 30˚С.

Требуется:

1. Раскрыть статическую неопределимость системы.

2. Определить из расчёта на прочность диаметры стержней.

3. *Определить начальные напряжения в стержнях, вызванные неточностью изготовления второго стержня, δ.

4. * Определить напряжения в стержнях, вызванные нагревом первого стержня, Δt.

-------------------------------------------------------------------------------------------------------------------------------

Решение

Пункт №1.

Под статически неопределимой понимают систему, реакции в опорах и внутренние усилия в элементах которой определить только с помощью уравнений равновесия статики невозможно. Для вычисления этих величин необходимо составить дополнительные уравнения. Их можно получить на основе анализа деформированной схемы рассматриваемой системы. Такие уравнения называют уравнениями перемещений (деформаций). Их можно так же назвать уравнениями совместности деформаций, поскольку они на основе геометрии деформированной системы отображают зависимость перемещений характерных точек системы, а значит неразрывность деформаций в системе. Число таких уравнений обусловлено степенью статической неопределимости системы. В основе вычисления степени статической неопределимости системы лежит выражение:

, (3.1)

где - степень статической неопределимости системы; - число связей, накладываемых на систему; - число уравнений равновесия статики.

Раскрытие статической неопределимости системы, то есть получение дополнительных уравнений и определение неизвестных величин, состоит из четырёх этапов. Рассмотрим их на данном примере.

Этап I. Статическая часть задачи (Статика). На этом этапе составляют уравнения равновесия статики для рассматриваемой системы.

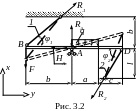
Рассматриваемая система фиксируется относительно основания в трёх опорных сечениях. Два опорных сечения расположены в месте шарнирного сопряжения стержней № 1 и № 2 с основанием. Опорное сечение A расположено в месте опирания абсолютно жёсткого стержня на шарнирно неподвижную опору (см. рис. 3.2).

В первую очередь покажем все реактивные силы, возникающие в опорах. Для этого проанализируем характер деформирования системы. Анализ действующей нагрузки позволяет сделать вывод, что абсолютно жёсткий брус под действием этой нагрузки должен повернуться относительно опорного сечения A против хода часовой стрелки. На рис. 3.2 показан характер деформирования системы. Следует отметить тот факт, что на самом деле перемещения характерных точек системы очень незначительны, возможно, незаметны невооружённым глазом или несоизмеримы с габаритными размерами системы. На рисунке масштаб параметров деформирования увеличен с тем, чтобы качественно оценить характер деформирования системы.

Такое поведение системы под действием заданной нагрузки приводит к появлению реакций и в местах шарнирной фиксации стержней с основанием. Обе реакции направлены вовне, поскольку оба стержня растягиваются (см. рис. 3.2). В опоре A возникает две составляющих реакции – вертикальная и горизонтальная, так как эта опора является шарнирно – неподвижной. Направим эти составляющие произвольно.

После того как все реактивные силы выявлены и представлены на схеме составим уравнения равновесия статики для рассматриваемой системы.

Пусть первое уравнение представляет собой сумму моментов всех сил относительно опорного сечения A.

; .

Второе уравнение представляет собой сумму проекций всех сил на ось x.

; .

Третье уравнение представляет собой сумму проекций всех сил на ось y.

; .

Мы составили три уравнения статики. Однако число неизвестных реакций – четыре. Следовательно, уравнений равновесия статики меньше, чем неизвестных. Значит задача является статически неопределимой. Степень статической неопределимости определим с помощью соотношения (3.1): .

Иными словами, задача один раз статически неопределима. И необходимо составить одно дополнительное уравнение, чтобы число неизвестных было равно числу уравнений.

На этом статическая часть задачи завершена.

Этап II. Геометрическая часть задачи (Геометрия). На этом этапе составляют дополнительные уравнения – уравнения перемещений рассматриваемой системы. В нашем случае необходимо одно уравнение перемещений. Составим его.

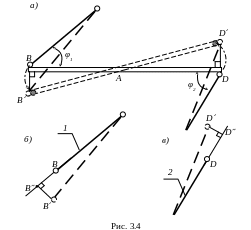
Для этого проанализируем, как переместились характерные точки системы. Этими точками являются точки, соответствующие местам шарнирного соединения абсолютно жёсткого бруса со стержнем № 1 (точка B) и стержнем № 2 (точка D) (рис. 3.3).

Выше мы уже выявили характер деформирования системы, согласно которому абсолютно жёсткий брус поворачивается относительно точки A против хода часовой точки. Значит, точки B и D должны описать по соответствующим направлениям дуги (это легко представить мысленно (рис. 3.4, а)). Однако мы знаем, что деформации системы весьма незначительны. Следовательно, эти дуги можно заменить на их хорды, то есть на отрезки, соединяющие крайние точки дуг. Кроме того, направим эти отрезки перпендикулярно первоначальному направлению абсолютно жёсткого бруса, как это показано на рис. 3.4, а. В итоге перемещения точек A и B определяются отрезками AA´ и BB´ (см. рис. 3.4, а). Мы получили два подобных треугольника ABB´ и ADD´ (см. рис. 3.4, a). А из подобия треугольников можно получить следующую зависимость:

, (3.2)

(см. рис. 3.3).

Теперь установим связь между перемещениями точек B и D и деформациями стержней 1 и 2, соответственно.

Перемещение точки B обуславливает деформацию стержня 1, а именно его удлинение (см. рис. 3.3). Для того чтобы графически показать абсолютное удлинение данного стержня проделаем следующие действия.

Покажем тонкой линией первоначальное направление первого стержня, например, как это показано на рис. 3.4, б. Мысленно совместим деформированный стержень 1 с недеформированным, то есть повернём его относительно шарнира по ходу часовой стрелки. В процессе совмещения точка B´ должна описать дугу. Не забывайте, что деформации и перемещения в рассматриваемой системе малы. А значит, мы можем опять заменить дугу прямым отрезком, причём направить его перпендикулярно первоначальному направлению первого стержня (см. рис. 3.4, б). В итоге получили новую точку B˝, расположенную на продолжении первого стержня в недеформированном состоянии. Получается, что удлиняется этот стержень на величину отрезка BB˝. То есть (см. рис. 3.3).

Аналогично получим точку D˝ для второго стержня (рис. 3.4, в). Соответственно второй стержень увеличивается в длине на величину отрезка DD˝. То есть его абсолютная продольная деформация: (см. рис. 3.3).

Теперь, чтобы установить связь между перемещениями и деформациями следует обратить внимание на треугольники и . Это два прямоугольных треугольника, у которых и являются гипотенузами, , - катетами, соответственно. Совместный анализ деформированной и недеформированной схем показывает, что и . Следовательно, , .

Подставив правые части полученных соотношений в уравнение перемещений (3.2), получим новое представление данного уравнения:

.

Этап III. Физическая часть задачи (Физика). На этом этапе описывают связь между деформационными характеристиками системы и прочностными.

В основе этой операции лежит закон Гука для конструктивного элемента: ,

где - продольная сила, действующая в стержневом элементе длиной с постоянной по длине площадью поперечного сечения , выполненном из материала с модулем упругости .

Теперь уравнение перемещений принимает вид:

.

Однако, по условию , то есть:

.

Анализ компонент полученного уравнения показал, что не заданными компонентами по условию задачи в нём являются длины стержней , и усилия в стержнях и . Длины стержней можно определить, исходя из геометрии системы. А именно:

, .

Усилия в стержнях относятся категории искомых величин. Согласно методу сечений (рис. 3.5):

, . (3.3)

Подставим все известные численные значения в полученное уравнение:

или , , .

В конечном итоге мы пришли к выражению вида: . (3.4)

Этап IV. Синтез. На этом этапе осуществляется совместное решение уравнений равновесия статики и уравнений перемещений.

В рассматриваемом случае три уравнения статики (см. Этап I) и одно уравнение перемещений (3.4).

С учётом выражений (3.3) и (3.4):

,

,

.

.

Согласно соотношению (3.4):

.

.

.

Определив все неизвестные, мы раскрыли статическую неопределимость системы.

Пункт №2.

Для того, чтобы определить диаметры стержней, следует определить площади их поперечных сечений и .

Так как стержни работают на центральное растяжение – сжатие, мы должны воспользоваться математическим выражением условия проектировочной задачи для данного вида нагружения:

. (3.5)

По длине стержней продольные силы не меняются, поскольку соотношения (3.3) действительны по всей длине как стержня 1, так и стержня 2.

Тогда с учётом соотношений (3.3) и условия (3.5) площади поперечных сечений стержней определим следующим образом:

, (по условию).

Теперь необходимо проверить выполнение условия прочности для второго стержня:

.

Вычислим процент недонапряжения:

.

Полученная величина значительно превышает допускаемые 9% недонапряжения: .

Возможно, если начать подбор сечений со второго стержня картина будет более благоприятной.

, .

Теперь проверим выполнение условия прочности для первого стержня:

, .

Вычислим процент перенапряжения:

.

Процент перенапряжения велик – на много больше допускаемых 5%, то есть: .

Естественно, следует остановиться на первом варианте определения площадей, когда

, .

Соответственно диаметры стержней будут следующие:

, .

, .

5