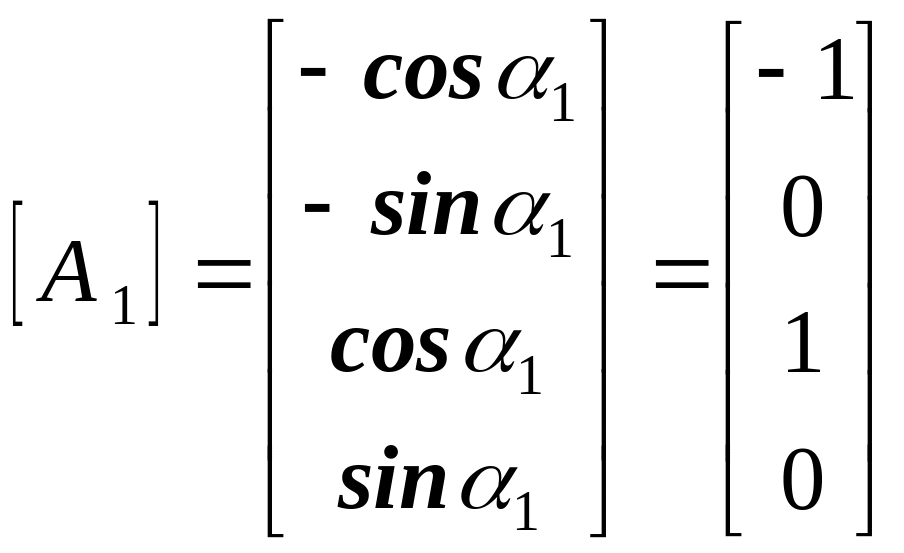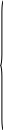Формирование уравнений равновесия фермы

1. Степени свободы системы и их нумерация

Каждый узел фермы имеет две поступательные степени свободы. Система, имеющая узлов, будет, таким образом, иметь 2n_p степеней свободы (от английского number of points).

Для каждого узла системы пронумеруем степени свободы (или компоненты перемещений) в следующем порядке: первым будем считать перемещение по оси , вторым – по оси . Степени свободы системы в целом будем нумеровать в порядке возрастания номеров узлов. Тогда первые 2 степени свободы относятся к первому узлу, следующие 2 (с третьей по четвертую) – ко второму и т.д.

Каждой степени свободы узла поставим в соответствие уравнения равновесия и , последовательность записи которых совпадает с нумерацией степеней свободы. Очевидно, что будем иметь 2n_p уравнений равновесия. Число всех степеней свободы обозначим . Здесь система координат X0Y – глобальная, т.е. одна для всей конструкции. Кроме глобальных осей существуют локальные оси - свои для каждого стержня фермы. Для определения направления локальных осей необходимо пронумеровать узлы фермы и для каждого стержня принять «начальный» (i) и «конечный» (j) узел. Локальная ось x_k каждого стержня направлена от «начального» узла к «конечному», имеет индекс, соответствующий номеру стержня, и обозначается с надчерком (рис.1).

2. Вектор внешних узловых сил

Е

y

сли по направлению –й степени свободы действует внешняя сила, то она войдет в –е уравнение равновесия. Причем сила будет иметь положительный знак, если ее направление совпадает с осью или . Если в направлении каждой степени свободы приложена соответствующая узловая сила , то вектор узловых сил имеет вид

где – внешние узловые усилия в направлении первой, второй и т.д. степеней свободы.

j

x_k

(1)

i

k

α

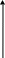
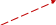
Рис. 1 x

3. Матрица равновесия системы

Составляя уравнения равновесия узлов в последовательности, соответствующей номерам степеней свободы, получим систему уравнений равновесия конструкции в целом. Силы, действующие на узел со стороны элементов, равны по величине и противоположны по знаку узловым силам, действующим на элемент. Неизвестными в уравнениях равновесия являются усилия в элементах и реакции в связях, а коэффициентами при неизвестных – компоненты матриц равновесия элементов и опорных связей. Свободными членами будут узловые внешние силы. Таким образом, система

статических уравнений имеет вид: .

(2)

Матрица равновесия системы имеет блочную структуру. Деление на блоки по горизонтали связано с тем, что для каждого узла плоской системы можно составить два уравнения равновесия. Следовательно, каждому узлу соответствует блок из двух строк. Деление на блоки по вертикали связано с элементами. Число столбцов равно числу элементов фермы плюс опорные связи. Каждый стержневой элемент соединяет два узла, поэтому усилие в нем входит в уравнения равновесия этих узлов.

Блок 1: начальный узел Блок 2: конечный узел Для шарнирно–стержневой системы матрица равновесия k-го элемента имеет вид: .

(3)

Матрица опорной связи имеет всего две строки:

(4)

Опорный узел

(4)

З десь α – угол наклона k –го стержня (от «начального» узла к «конечному) к оси x, либо наклон опорной связи. По сути это угол наклона между локальной осью x каждого стержня и глобальной осью x (рис.1). Значения направляющих косинусов элемента, соединяющего узлы i и j, удобно определять через координаты его узлов по формулам:

; , где

(5)

x_i y_i x_j y_j - координаты «начального» (i -го) и «конечного» (j -го) узлов в глобальной системе координат. Матрица равновесия системы состоит из матриц равновесия элементов Учитывая блочную структуру матриц, можно записать

,

(6)

где – общее число элементов и опорных связей.

В статически определимых системах число неизвестных усилий равно числу уравнений равновесия, поэтому матрица - квадратная. Если конструкция неизменяемая, то матрица равновесия невырождена и имеет обратную. Вектор усилий можно определить из решения системы уравнений (2). С помощью обратной матрицы

решение можно записать:

(7)

Решаем систему уравнений равновесия рамы с помощью обращения матрицы и определяем компоненты внутренних усилий

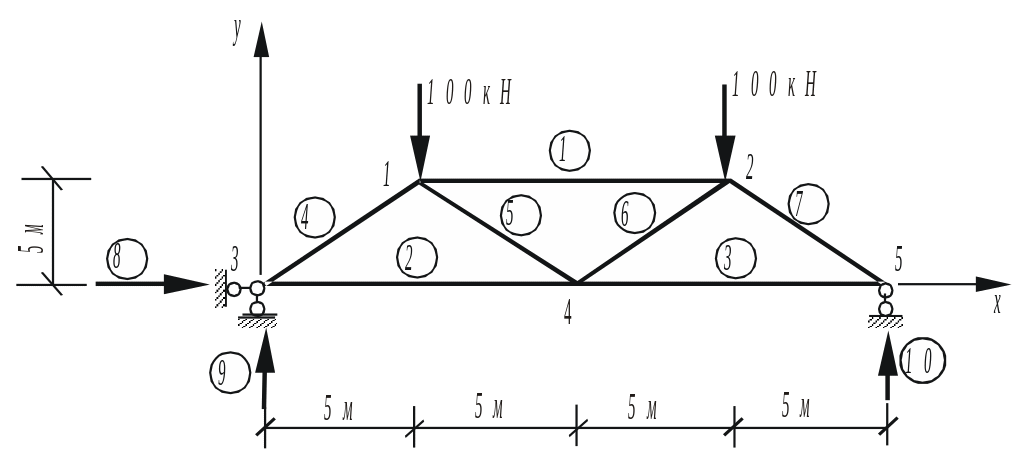
Пример. Для фермы, изображенной на рис. 2, получить матрицу равновесия, определить усилия в стержнях и опорные реакции.

Основные этапы расчета следующие:

Нумеруем узлы фермы (с 1 по 5). Нумеруем стержни фермы и опорные связи ( = 1 … 10). За начальный узел i каждого стержня возьмем узел с наименьшим порядковым номером. Конечный узел - j. Так, для стержня 6 начальный узел – 2, конечный – 4.

Определяем длину стержней, направляющие синусы и косинусы по выражениям (5)

	СТЕРЖНИ							ОПОРЫ
	1	2	3	4	5	6	7	8	9	10
xi	4	0	8	4	4	12	12
xj	12	8	16	0	8	8	16
l x	8	8	8	-4	4	-4	4
yi	3	0	0	3	3	3	3
yj	3	0	0	0	0	0	0
l y	0	0	0	-3	-3	-3	-3
l	8	8	8	5	5	5	5
Cos α	1	1	1	-0,8	0,8	-0,8	0,8	1	0	0
Sin α	0	0	0	-0,6	-0,6	-0,6	-0,6	0	1	1

Н а примере стержней 1 (1-2) и 4 (1-3) покажем формирование матрицы равновесия в редуцируемой (сжатой) форме. Локальные оси для этих стержней (x₁ и x₄) показаны пунктиром.

	Блок 1: узел 1 Блок 2: узел 2 Блок 1: узел 1 Блок 2: узел 3
М Блок 1: узел 5 атрица равновесия опорной связи в пятом узле:

Матрица равновесия для всей фермы приведена в табл. 1

Таблица 1. Матрица равновесия фермы и вектор внешних узловых сил

Номера узлов	Номера уравнений	Номера стержней
		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
1	1	-1			0,8	-0,8
	2	0			0,6	0,6						-100
2	3	1					0,8	-0,8
	4	0					0,6	0,6				-100
3	5		-1		-0,8				-1	0
	6		0		-0,6				0	-1
4	7		1	-1		0,8	-0,8
	8		0	0		-0,6	-0,6
5	9			1				0,8			0
	10			0				-0,6			-1

Строки табл. 1 попарно соответствуют узлам, а столбцы – стержням. Для каждого узла 2 строки: первая - соответствует уравнению , а вторая - . Незаполненные элементы таблицы соответствуют нулевым элементам матрицы и вектора

Используя обратную матрицу , определим усилия в стержнях фермы

, -0,5 0,666667 0,5 0,666667 0 0 0 1,333333 0 0 0 0,75 -1 0,75 -0,33333 0 0 1 -0,66667 1 0 -100 0,25 -0,33333 0,25 -1 0 0 0 -0,66667 1 0 0 0,3125 1,25 0,3125 0,416667 0 0 0 0,833333 0 0 -100 -0,3125 0,416667 -0,3125 -0,41667 0 0 0 -0,83333 0 0 0 0,3125 -0,41667 0,3125 0,416667 0 0 0 -0,83333 0 0 0 -0,3125 0,416667 -0,3125 1,25 0 0 0 0,833333 0 0 0 -1 0 -1 0 -1 0 -1 0 -1 0 0 -0,1875 -0,75 -0,1875 -0,25 0 -1 0 -0,5 0 0 0 0,1875 -0,25 0,1875 -0,75 0 0 0 -0,5 0 -1 0
		УСИЛИЯ
		-133,333	1
		133,3333	2
		133,3333	3
	=	-166,667	4
		0	5
		0	6
		-166,667	7
		0	8
		100	9
		100	10

5