
- •Расчетно-графическая работа № 2.
- •Задача № 1.
- •*Проверить выполнение условия прочности и вычислить запас пере- или недонапряжения, исходя из предположения, что стержень выполнен из хрупкого материала.
- •*Переопределить диаметры ступеней стержня на основе условия прочности, исходя из предположения, что стержень выполнен из хрупкого материала.
- •Решение
Расчетно-графическая работа № 2.
Расчёт стержней и стержневых систем на растяжение сжатие.
Задача № 1.
Расчёт статически определимого стержня.
Дано:
стержень, состоящий из трёх ступеней
круглого поперечного сечения (рис. 1.1,
а); начальные диаметры ступеней:
![]() ,
,
![]() ,
,
![]() ;
длины ступеней:
;
длины ступеней:
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ;
материалы: СЧ12 -
;
материалы: СЧ12 -
![]() ,
,
![]() ;
Ст3 -
;
Ст3 -
![]() ,
,
![]() ;
коэффициенты запаса прочности: для
хрупкого материала
;
коэффициенты запаса прочности: для
хрупкого материала
![]() ,
для пластичного материала
,
для пластичного материала
![]()
Требуется:
Построить эпюру продольной силы э «N».
Построить эпюру нормальных напряжений.
Проверить выполнение условия прочности и вычислить запас пере- или недонапряжения, исходя из предположения, что стержень выполнен из пластичного материала.
*Проверить выполнение условия прочности и вычислить запас пере- или недонапряжения, исходя из предположения, что стержень выполнен из хрупкого материала.
Переопределить диаметры ступеней стержня на основе условия прочности, исходя из предположения, что стержень выполнен из пластичного материала.
*Переопределить диаметры ступеней стержня на основе условия прочности, исходя из предположения, что стержень выполнен из хрупкого материала.
Определить перемещение свободного сечения стержня для случая пластичного материала.
-------------------------------------------------------------------------------------------------------------------------------
Решение
Пункт №1.
В основе построения эпюры продольных сил лежит «метод сечений» (или метод РОЗУ). Он состоит из четырёх этапов (см. лекции):
1-ый этап – разрезаем стержень, на который действует система статически уравновешенных сил, плоскостью, перпендикулярной продольной оси стержня, в точке с координатой z (имеется в виду, что ось z совпадает с продольной осью стержня). В результате получаем сечение с координатой z;
2-ой этап – отбрасываем наиболее загруженную часть стержня, расположенную либо с одной, либо с другой стороны от рассматриваемого сечения с координатой z;
3-ий этап – заменяем
действие отброшенной части на оставшуюся
продольной силой,
![]() .
Такое обозначение продольной силы
объясняется тем, что в общем случае она
является функцией от координаты сечения.
Иными словами, величина и направление
продольной силы зависит от рассматриваемого
сечения;
.
Такое обозначение продольной силы
объясняется тем, что в общем случае она
является функцией от координаты сечения.
Иными словами, величина и направление
продольной силы зависит от рассматриваемого
сечения;
4-ый этап – уравновешиваем систему сил, действующих на оставшуюся часть. В состав данной системы входит нагрузка, действующая на рассматриваемую часть стержня, и продольная сила . Математически состояние равновесия опишем с помощью уравнения равновесия в виде проекций сил, принадлежащих оставшейся части стержня, на его продольную ось. Принимают, что направление вектора продольной силы совпадает с направлением внешней нормали. Причём уравнение принято составлять таким образом, чтобы продольная сила располагалась в левой части уравнения, а проекции оставшихся из заданных сил – в правой части уравнения.
Знаки проекций сил, действующих на оставшуюся часть стержня, определяются в соответствии с определённым правилом знаков.
Правило знаков: если заданная нагрузка действует в направлении от рассматриваемого сечения в сторону оставшейся части стержня (то есть стремиться растянуть оставшуюся часть стержня), то знак у проекции положительный; если напротив (то есть стремиться сжать оставшуюся часть стержня), то знак у проекции отрицательный. При этом мы мысленно придерживаем оставшуюся часть стержня за рассматриваемое сечение.
Если результирующая суммы проекций
окажется положительной
![]() ,
значит, направление продольной силы
остаётся неизменным, то есть по направлению
внешней нормали. Иными словами, продольная
сила растягивающая, следовательно, в
окрестности рассматриваемого сечения
стержень растягивается. И наоборот.
,
значит, направление продольной силы
остаётся неизменным, то есть по направлению
внешней нормали. Иными словами, продольная
сила растягивающая, следовательно, в
окрестности рассматриваемого сечения
стержень растягивается. И наоборот.
Теперь воспользуемся методом сечений и построим эпюру продольной силы для рассматриваемого стержня. Однако метод сечений можно применить для случая, когда на стержень действует статически уравновешенная система сил. В связи, с чем необходимо нагрузку, действующую на стержень, уравновесить реактивной силой, возникающей в заделке. Для этого её следует выявить, определить её величину и направление. В общем случае в заделке возникает шесть составляющих реакции (по числу степеней свободы сечения в пространстве). Однако в рассматриваемом случае активной является только одна составляющая – реактивная сила, направленная вдоль продольной оси. Это обусловлено направлением заданной нагрузки (см. рис. 1.1, а). Она вся действует параллельно оси стержня.
 Составим
уравнение равновесия статики в виде
суммы проекций всех сил на продольную
ось стержня, равную нулю. Если предположить,
что продольная ось стержня совпадает
с осью координат z
(рис. 1.1, а), то:
Составим
уравнение равновесия статики в виде
суммы проекций всех сил на продольную
ось стержня, равную нулю. Если предположить,
что продольная ось стержня совпадает
с осью координат z
(рис. 1.1, а), то:
![]()
Знак «-» в полученном результате говорит о том, что истинное направление реакции противоположно тому, которым мы задались изначально. Значит необходимо поменять заданное направление на противоположное, как это показано на рис. 1.1, а. При этом знак «-» в численном значении исчезает, поскольку направление стало совпадать с истинным направлением. Теперь расчётная схема принимает вид, показанный на рис. 1.1, б.
После того, как система сил, действующих
на стержень, уравновешена, начинаем
строить эпюру продольной силы, э «N».
Для начала определим число участков, в
пределах каждого из которых продольная
сила меняется по одному закону. Поскольку
продольная сила зависит только от
заданной нагрузки и никак не зависит
от размеров и формы поперечного сечения,
в рассматриваемом стержне три участка
длиной
![]() ,
,
![]() и
и
![]() .
.
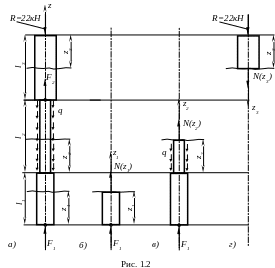 Рассмотрим
первый участок. Пусть первым участком
будет участок длиной
.
Выполняем первое действие метода
сечений: разрезаем стержень на первом
участке. В результате чего получаем
сечение с координатой
Рассмотрим
первый участок. Пусть первым участком
будет участок длиной
.
Выполняем первое действие метода
сечений: разрезаем стержень на первом
участке. В результате чего получаем
сечение с координатой
![]() (см. рис. 1.1, б;
рис. 1.2, а). Данная координата
берётся относительно локальной системы
координат с началом отсчёта в начале
участка. Выбор начала участка зависит
от того, какую часть стержня, относительно
сечения мы отбросим (с какой стороны от
сечения). Как правило, отбрасывают
наиболее загруженную часть элемента.
Значит, в нашем случае отбрасываем часть
стержня, расположенную выше сечения.
Поэтому начало локальных координат
расположим в нижнем сечении (рис. 1.2, б).
На этапе мысленного отбрасывания
какой-либо части элемента «не мысленно»
обозначаем аналитически границы, в
которых будет изменяться координата
сечения
:
(см. рис. 1.1, б;
рис. 1.2, а). Данная координата
берётся относительно локальной системы
координат с началом отсчёта в начале
участка. Выбор начала участка зависит
от того, какую часть стержня, относительно
сечения мы отбросим (с какой стороны от
сечения). Как правило, отбрасывают
наиболее загруженную часть элемента.
Значит, в нашем случае отбрасываем часть
стержня, расположенную выше сечения.
Поэтому начало локальных координат
расположим в нижнем сечении (рис. 1.2, б).
На этапе мысленного отбрасывания
какой-либо части элемента «не мысленно»
обозначаем аналитически границы, в
которых будет изменяться координата
сечения
:
![]() .
.
Теперь заменяем действие отброшенной
части стержня на рассматриваемую
продольной силой
![]() (см. рис. 1.2, б).
(см. рис. 1.2, б).
После этого необходимо уравновесить систему сил, действующих на рассматриваемую часть стержня.
![]() ,
,
![]() .
.
Правило составления уравнения см. выше. Полученное выражение представляет собой уравнение прямой, параллельной оси, по которой откладываются аргументы функции, в нашем случае это координаты сечения z1. При построении эпюры такую ось называют базовой осью эпюры.
Теперь, рассуждая аналогично, получим уравнение, определяющее продольную силу на втором участке (рис. 1.2, в).
![]() ,
,
![]() .
.
Для второго участка начало локальной
системы координат располагается в его
начале. Так как была отброшена часть
стержня расположенная выше сечения
(см. рис. 1.2, в), то начало участка
располагается в сечении, примыкающем
к границе между первой и второй ступенями.
Длина исследуемого участка на оставшейся
части стержня составляет отрезок
координатной оси, равный
![]() (см. рис. 1.2, в). Поэтому при составлении
уравнения для продольной силы
(см. рис. 1.2, в). Поэтому при составлении
уравнения для продольной силы
![]() равнодействующую от распределённой
нагрузки мы определили как
равнодействующую от распределённой
нагрузки мы определили как
![]() .
Правило знаков для составления уравнения
было представлено выше.
.
Правило знаков для составления уравнения
было представлено выше.
Чтобы получить уравнение, определяющее продольную силу на третьем участке, рассечем, третью ступень и теперь отбросим часть стержня, распложенную ниже сечения (рис. 1.2, г). Тогда уравнение продольной силы получиться следующим:
![]() ,
,
![]() .
.
В данном случае продольная сила не изменяется по длине третьего участка. Это значит, что графически продольная сила определяется прямой, параллельной базовой оси эпюры.
На основе полученных аналитических данных построим эпюру продольной силы (рис. 1.1, в).
Первый пункт работы выполнен.
Пункт №2.
Для того, чтобы построить эпюру нормальных напряжений, воспользуемся формулой для определения нормальных напряжений в любой точке произвольного сечения стержня:
![]() ,
(1.1)
,
(1.1)
где N – продольная
сила, действующая в поперечном сечении
стержня с площадью A,
в котором требуется определить нормальные
напряжения
![]() .
Из соотношения (1.1) следует, что нормальные
напряжения при данном виде нагружения
не зависят от координаты точки в сечении,
в котором они определяются и распределены
равномерно по всему сечению. Их величина
зависит от значения продольной силы и
площади поперечного сечения. При этом
характер зависимости от координаты
сечения качественно остаётся таким же
как и у продольной силы. Поэтому, эпюру
нормальных напряжений можно построить
по характерным сечениям. Такие сечения
для рассматриваемого случая показаны
на рис. 1.1, а (они пронумерованы). Под
характерными понимаются сечения,
примыкающие к границам ступеней, то
есть, где происходит изменение площади
поперечного сечения, и сечения, примыкающие
к границам участков, то есть, где меняется
закон изменения продольной силы.
.
Из соотношения (1.1) следует, что нормальные
напряжения при данном виде нагружения
не зависят от координаты точки в сечении,
в котором они определяются и распределены
равномерно по всему сечению. Их величина
зависит от значения продольной силы и
площади поперечного сечения. При этом
характер зависимости от координаты
сечения качественно остаётся таким же
как и у продольной силы. Поэтому, эпюру
нормальных напряжений можно построить
по характерным сечениям. Такие сечения
для рассматриваемого случая показаны
на рис. 1.1, а (они пронумерованы). Под
характерными понимаются сечения,
примыкающие к границам ступеней, то
есть, где происходит изменение площади
поперечного сечения, и сечения, примыкающие
к границам участков, то есть, где меняется
закон изменения продольной силы.
Определим нормальные напряжения в
характерных сечениях. При этом формулу
(1.1) дополним следующими обозначениями:
![]() ,
i – номер характерного
сечения, в котором определяются нормальные
напряжения;
,
i – номер характерного
сечения, в котором определяются нормальные
напряжения;
![]() - продольная сила, действующая в сечении
с номером i;
- продольная сила, действующая в сечении
с номером i;
![]() - площадь сечения с номером i.
- площадь сечения с номером i.
Чтобы выполнить вычисления необходимо
определить площади поперечных сечений
ступеней стержня:
![]() ,
где k – номер ступени.
,
где k – номер ступени.
![]() ;
;
![]() ;
;
![]() .
.
Теперь, чтобы воспользоваться формулой (1.1) нужно правильно определить числитель и знаменатель. Числитель определяется с помощью эпюры N или на основании уравнений продольной силы. В знаменатель подставляется значение поперечного сечения ступени, которой принадлежит характерное сечение.
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Строим эпюру нормальных напряжений по точкам (рис. 1.1, г).
Второй пункт работы выполнен.
Пункт №3.
Исходя из предположения, что рассматриваемый стержень выполнен из пластичного материала, параметры которого указаны в исходных данных, необходимо определить, выполняется ли условие прочности. Иными словами требуется решить проверочную задачу. Для случая пластичных материалов она имеет вид:
![]() .
.
Поскольку считается, что пластичные
материалы одинаково сопротивляются
внешним воздействиям, вызывающим как
растяжение, так и сжатие, то в левую
часть неравенства подставляется
абсолютная максимальная величина
расчётного напряжения. В данном случае
её можно определить по эпюре нормальных
напряжений (см. рис 1.1, г). В нашем
случае максимальными по модулю являются
сжимающие напряжения, они составляют
![]() .
.
Допускаемые напряжения определяются с помощью экспериментальных данных. А, именно, допускаемые напряжения для пластичных материалов определяют на основе предела текучести (см. лаб. раб.). В данном примере используется материал с пределом текучести, составляющем , коэффициент запаса прочности равен . Тогда допускаемые напряжения:
![]() .
.
Теперь подставим соответствующие значения в правую и левую части условия прочности:
![]() .
.
Условие прочности выполняется. Определим
процент недонапряжения
![]() :
:
![]() .
.
Знак «-» обусловлен тем, что при недонапряжении максимальные расчётные напряжения меньше допускаемых напряжений. В знаменатель всегда ставится величина, с которой сравнивается расчётная величина.
В нашем случае процент недонапряжения велик, он превышает допускаемые 9% недонапряжения в несколько раз. Иными словами, материал расходуется неэффективно.
Третий пункт работы выполнен.
Пункт №4. (Данный пункт относится к категории необязательных)
Теперь предположим, что стержень выполнен из хрупкого материала, характеристики которого приведены в исходных данных. Проверим для этого случая выполнение условия прочности, которое теперь принимает вид:
![]() ,
,
![]() .
.
Здесь
![]() - максимальные растягивающие напряжения
во всём стержне,
- максимальные растягивающие напряжения
во всём стержне,
![]() - максимальные сжимающие напряжения во
всём стержне.
- максимальные сжимающие напряжения во
всём стержне.
Для хрупкого материала допускаемые напряжения определяются на основе информации о пределе прочности, то есть в нашем случае:
![]() ,
,
![]()
С помощью эпюры определяем максимальные
растягивающие и максимальные сжимающие
напряжения:
![]() ,
,
![]() .
Теперь подставляем полученные значения
в условие прочности:
.
Теперь подставляем полученные значения
в условие прочности:
![]() ,
,
![]() .
.
В области растянутого материала условие прочности не выполняется, то есть имеет место перенапряжение. Определим процент перенапряжения :
![]()
В данном случае полученный процент перенапряжения значительно превышает допускаемую величину в 5%. Это значит для хрупкого материала, что данный стержень потеряет свою целостность в области опасного сечения при нагрузке, значительно меньшей, чем расчётная.
Для сжатого материала условие прочности выполняется, причём с большим запасом прочности:
![]() .
.
Процент недонапряжения во много раз превышает допускаемые 9%.
Четвёртый пункт работы выполнен.
Пункт №5.
Теперь попробуем с учётом условия прочности подобрать новые диаметры поперечных сечений ступеней стержня, полагая, что материал пластичный. А именно, по условию это сталь Ст3. Иначе говоря, требуется решить проектировочную задачу на основе условия прочности.
В развёрнутом виде, то есть с учётом выражения (1.1), условие прочности для пластичных материалов принимает вид:
![]() .
.
Тогда условие проектировочной задачи принимает вид:
![]() .
.
Используя эпюру продольной силы,
определим диаметры ступеней. Причём
интерес представляет максимальная по
модулю продольная сила в пределах
ступени, площадь которой требуется
определить (![]() ,
,
![]() ,
,
![]() - площади поперечных сечений первой,
второй, третьей ступеней стержня). Тогда:
- площади поперечных сечений первой,
второй, третьей ступеней стержня). Тогда:
![]() ;
;
![]() ;
;
![]() .
.
![]() ,
,
![]() ,
,
![]() - максимальные по модулю значения
продольной силы на первой, второй,
третьей ступенях.
- максимальные по модулю значения
продольной силы на первой, второй,
третьей ступенях.
Так как
![]() ,
то
,
то
![]() .
Поэтому новые значения диаметров
ступеней:
.
Поэтому новые значения диаметров
ступеней:
![]() ;
;
![]() ;
;
![]() .
.
Необходимо отметить, что для первой и второй ступеней из условия прочности были подобраны одинаковые диаметры. То есть оптимальным с позиции прочностной надёжности будет стержень, эскиз которого представлен на рис. 1.3, б.
Для сравнения на этом же рисунке показан исходный стержень (рис. 1.3, а). В данном случае для наглядности используется условный масштаб. Он позволяет оценить соотношение величин площадей поперечных сечений ступеней рассматриваемого варианта стержня между собой.
Пятый пункт работы выполнен.
Пункт №6. (Данный пункт относится к категории необязательных)
Теперь подберём диаметры поперечных сечений ступеней рассматриваемого стержня, исходя из предположения, что он выполнен из хрупкого материала.
С учётом выражения (1.1) условие прочности для хрупких материалов в развёрнутом виде принимает вид:
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() - максимальные алгебраические значения
растягивающей и сжимающей продольных
сил;
- максимальные алгебраические значения
растягивающей и сжимающей продольных
сил;
![]() ,
,
![]() - предельные значения площадей поперечных
сечений, обусловленные растяжением и
сжатием материала, соответственно.
Тогда условие проектировочной задачи
принимает вид:
- предельные значения площадей поперечных
сечений, обусловленные растяжением и
сжатием материала, соответственно.
Тогда условие проектировочной задачи
принимает вид:
![]() ,
,
![]() .
.
Определим значения площадей поперечных сечений ступеней рассматриваемого стержня:
![]() - не имеет решения, поскольку в первой
ступени нет растягивающей продольной
силы (
- не имеет решения, поскольку в первой
ступени нет растягивающей продольной
силы (![]() ).
).
![]() ;
;
![]() ;
;
![]() ;
;
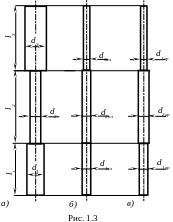
![]() - не имеет решения, поскольку в третьей
ступени нет растягивающей продольной
силы (
- не имеет решения, поскольку в третьей
ступени нет растягивающей продольной
силы (![]() );
);
![]() .
.
![]() ,
,
![]() - максимальные алгебраические значения
растягивающей и сжимающей продольных
сил на i – ой ступени;
- максимальные алгебраические значения
растягивающей и сжимающей продольных
сил на i – ой ступени;
![]()
![]() - предельные значения площадей поперечных
сечений, обусловленные растяжением и
сжатием материала для i
– ой ступени; i=1,2,3.
- предельные значения площадей поперечных
сечений, обусловленные растяжением и
сжатием материала для i
– ой ступени; i=1,2,3.
Естественно из двух расчётных значений площади поперечного сечения ступени следует выбрать максимальное, поскольку при выборе минимального значения в одном из двух вариантов условия прочности нестрогое неравенство выполняться не будет.
Для первой и третьей ступеней активным
из двух неравенств было только одно
(условие прочности при сжатии) поэтому
и расчётным получилось только одно
значение площади для каждой ступени.
Для ступени, второй, активными оказались
оба неравенства, так как материал ступени
претерпевает и растяжение, и сжатие
(см. рис. 1.1, в). Поэтому расчёт дал
два значения площади поперечного сечения
второй ступени: при растяжении -
![]() и при сжатии -
и при сжатии -
![]() .
Большим является значение площади,
обусловленное растяжением, его и
принимаем для второй ступени
рассматриваемого стержня.
.
Большим является значение площади,
обусловленное растяжением, его и
принимаем для второй ступени
рассматриваемого стержня.
Тогда диаметры ступеней:
![]() ;
;
![]() ;
;
![]() .
.
Эскиз стержня представлен на рис. 1.3, в.
Шестой пункт работы выполнен.
Пункт №7.
Определим перемещение
![]() крайнего свободного (то есть не
заделанного) сечения рассматриваемого
стержня для случая пластичного материала.
Данное сечение переместится на столько,
на сколько продольно деформируется
стержень. То есть
крайнего свободного (то есть не
заделанного) сечения рассматриваемого
стержня для случая пластичного материала.
Данное сечение переместится на столько,
на сколько продольно деформируется
стержень. То есть
![]() ,
,
![]() - абсолютная продольная деформация
стержня,
- абсолютная продольная деформация
стержня,
![]() - общая длина стержня.
- общая длина стержня.
Если
![]() ,
то
,
то
![]() .
То есть абсолютная продольная деформация
стержня равна сумме абсолютных продольных
деформаций его ступеней.
.
То есть абсолютная продольная деформация
стержня равна сумме абсолютных продольных
деформаций его ступеней.
Для определения абсолютной продольной деформации участка длиной l можно воспользоваться выражением закона Гука для конструктивного элемента:
![]() ,
(1.2)
,
(1.2)
где
![]() - продольная сила, действующая в сечениях
с площадью A; l
– длина деформируемого участка; E
– модуль Юнга материала, из которого
выполнен участок.
- продольная сила, действующая в сечениях
с площадью A; l
– длина деформируемого участка; E
– модуль Юнга материала, из которого
выполнен участок.
Следует отметить тот факт, что данная формула действует, когда продольная сила в пределах рассматриваемого участка является константой. В рассматриваемом примере продольная сила неизменна в пределах первой и третьей ступеней (см. рис. 1.1, в). Во второй ступени продольная сила меняется. Значит формулой (1.2) пользоваться для определения продольной деформации этой ступени нельзя.
Тогда используют другой подход для
определения деформации. Рассмотрим его
на примере второй ступени. Предположим,
что вторая ступень, длина которой
![]() (рис. 1.4, а), представляет собой
совокупность элементов длиной
(рис. 1.4, а), представляет собой
совокупность элементов длиной
![]() и площадью
и площадью
![]() (рис. 4, б). Ввиду малости длины каждого
элемента можно полагать, что продольная
сила по длине каждого элемента не
меняется (см. рис. 1.4, б). Тогда удлинение
каждого элемента согласно (1.2):
(рис. 4, б). Ввиду малости длины каждого
элемента можно полагать, что продольная
сила по длине каждого элемента не
меняется (см. рис. 1.4, б). Тогда удлинение
каждого элемента согласно (1.2):
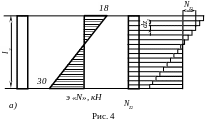
![]() .
.
Если просуммировать удлинения всех
элементарных участков, из которых
состоит ступень два, то получим удлинение
всей ступни:
![]() .
.
С позиций высшей математики просуммировать удлинения всех элементарных участков ступни это означает проинтегрировать выражение, определяющее удлинение одного элемента, в пределах длины ступени:
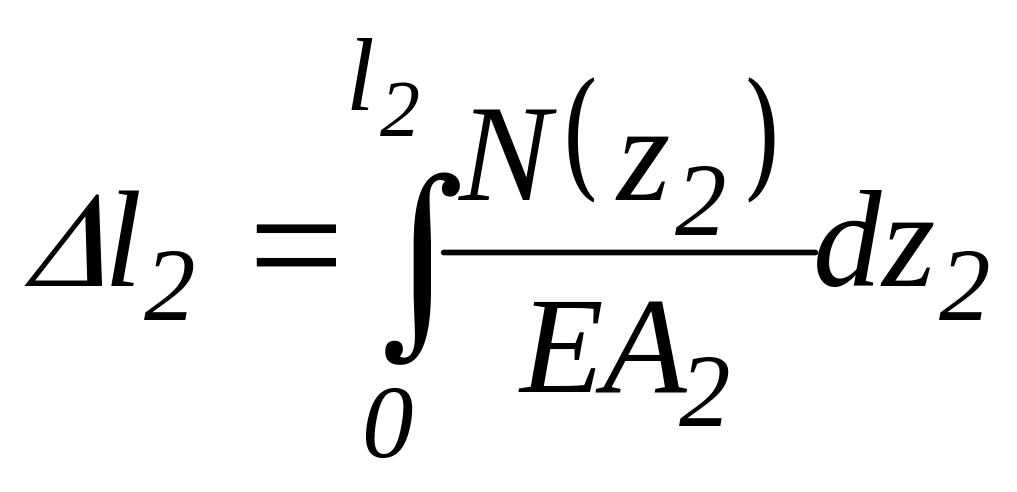 .
.
Эти рассуждения неизменны всегда при определении продольной деформации участка, по длине которого распределена нагрузка, то есть участка, по длине которого продольная сила меняется. Тогда в общем виде соотношение, определяющее продольную деформацию подобного участка примет вид:
 .
.
Если предположить, что в пределах длины l участка и материал, и размеры, и форма поперечного сечения остаются неизменными, то:
 ,
(1.3)
,
(1.3)
где i– номер участка.
Формализуем подход определения количества
участков, для каждого из которых будет
составляться выражение(1.3). Для этого
необходимо учитывать, сколько раз
меняется закон, описывающий продольную
силу, сколько раз меняется площадь
поперечного сечения и сколько раз
меняется материал. Поскольку соотношение,
определяющее изменение длины
![]() ,
учитывает характеристики материала,
из которого изготовлен участок длиной
,
учитывает характеристики материала,
из которого изготовлен участок длиной
![]() ,
величину площади поперечного сечения
,
величину площади поперечного сечения
![]() и закон изменения продольной силы
и закон изменения продольной силы
![]() .
Иными словами в пределах одного участка
продольная сила должна определяться
одним уравнением, площадь поперечного
сечения должна быть неизменной, участок
должен быть выполнен из одного материала.
С учётом всех этих требований количество
участков в рассматриваемом стержне
остаётся равным трём, о чём говорилось
выше. То есть оно совпадает с числом
ступеней.
.
Иными словами в пределах одного участка
продольная сила должна определяться
одним уравнением, площадь поперечного
сечения должна быть неизменной, участок
должен быть выполнен из одного материала.
С учётом всех этих требований количество
участков в рассматриваемом стержне
остаётся равным трём, о чём говорилось
выше. То есть оно совпадает с числом
ступеней.
Теперь руководствуясь рассуждениями, приведёнными выше, определим изменения длин всех участков.
Определим изменение длины первого участка (см. соотношение (1.2)):
![]()
Определим изменение длины второго участка, то есть второй ступени. В пределах второй ступени продольная сила непостоянна (о чём говорилось выше). Следовательно, необходима процедура интегрирования согласно формуле (1.3):
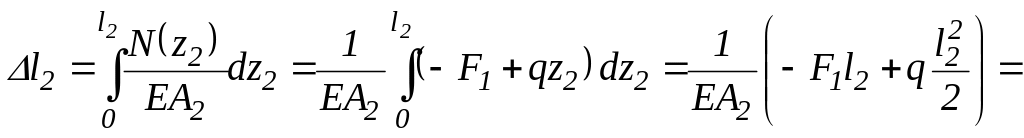
![]() .
.
Для третьего участка опять воспользуемся соотношением (1.2), поскольку для этого участка неизменны не только площадь поперечного сечения и материал, но и продольная сила (см. рис. 1.1, в).
![]()
Тогда весь стержень деформируется на величину:
![]() .
.
Знак «-» говорит о том, что в результате деформации длина стержня уменьшается, а значит крайнее нижнее сечение переместится вверх на величину абсолютной продольной деформации:
,
![]()
Существует другой способ определения
деформации участков стержня, минуя
процедуру интегрирования. В его основе
так же лежит выражение (1.2). Необходимо
помнить, что продольная 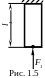 сила
– это внутренний силовой фактор, а
значит она обусловлена внешними
нагрузками. Причём, используя принцип
независимости действия сил и метод
сечений, можно установить однозначную
зависимость между каждой составляющей
внешней нагрузки и продольной силой.
Рассмотрим это на примере нашего стержня.
сила
– это внутренний силовой фактор, а
значит она обусловлена внешними
нагрузками. Причём, используя принцип
независимости действия сил и метод
сечений, можно установить однозначную
зависимость между каждой составляющей
внешней нагрузки и продольной силой.
Рассмотрим это на примере нашего стержня.
Начнём с первой ступени. Мысленно её
отсекаем от стержня и в месте рассечения
жёстко фиксируем ступень (рис. 1.5). Теперь
воспользуемся соотношением (1.2). Продольная
сила в сечениях этой ступени обусловлена
только силой
![]() и равна
и равна
![]() ,
поскольку сила стремиться сжать участок
длиной
,
поскольку сила стремиться сжать участок
длиной
![]() .
В этом случае продольная деформация
ступени составит:
.
В этом случае продольная деформация
ступени составит:
![]() .
.
В итоге мы получили результат, совпадающий с тем, который был получен выше.
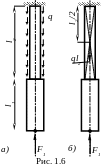 Вторая
ступень будет деформироваться от
действия силы
Вторая
ступень будет деформироваться от
действия силы
![]() и от распределённой нагрузки по самой
второй ступени (рис. 1.6, а). Продольная
сила, возникающая в сечениях второй
ступени от силы
и от распределённой нагрузки по самой
второй ступени (рис. 1.6, а). Продольная
сила, возникающая в сечениях второй
ступени от силы
![]() равна
равна
![]() ,
от распределённой нагрузки по второй
ступени -
,
от распределённой нагрузки по второй
ступени -
![]() .
Необходимо помнить, что распределённая
нагрузка по второй ступени (то есть
исследуемой ступени) схематизируется
в виде сосредоточенной силы, прикладываемой
по центру второй ступени (рис. 1.6, б).
Так как она равна равнодействующей
равномерно распределённой по второй
ступени нагрузки. Поэтому она деформирует
участок ступени длиной
.
Необходимо помнить, что распределённая
нагрузка по второй ступени (то есть
исследуемой ступени) схематизируется
в виде сосредоточенной силы, прикладываемой
по центру второй ступени (рис. 1.6, б).
Так как она равна равнодействующей
равномерно распределённой по второй
ступени нагрузки. Поэтому она деформирует
участок ступени длиной
![]() .
Тогда согласно соотношению (1.2) изменения
длины второй ступени от выше перечисленных
внешних силовых факторов в отдельности
составят:
.
Тогда согласно соотношению (1.2) изменения
длины второй ступени от выше перечисленных
внешних силовых факторов в отдельности
составят:
![]() ,
,
![]() .
.
 На
основании принципа независимости
действия сил суммарная деформация
составит:
На
основании принципа независимости
действия сил суммарная деформация
составит:
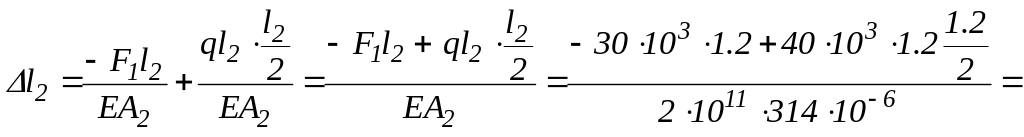
![]() .
.
Сравните полученный данным способом результат с результатом, полученным через интегрирование.
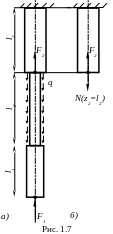
Деформацию третьей ступени вызывают
сила
,
распределённая по второй ступени
нагрузка
![]() и сила
и сила
![]() (рис. 1.7, а). При этом составляющие
продольной силы в сечениях третей
ступени от этих компонент внешней
нагрузки:
(рис. 1.7, а). При этом составляющие
продольной силы в сечениях третей
ступени от этих компонент внешней
нагрузки:
![]() ,
,
![]() ,
,
![]() .
.
Тогда доли деформации ступени от этих факторов составят:
![]() ,
,
![]() ,
,
![]()
А суммарная деформация:
![]()
![]()
![]() .
.
Так же можно было заменить действие первой и второй ступеней на третью продольной силой, действующей в последнем сечении второго участка (ступени), как это показано на рис. 1.7, б. И тогда продольная деформация третьего участка будет определяться выражением вида:
![]()
Тогда:
, .
Для выполнения пункта №7 можно воспользоваться любым удобным подходом.
