1.4. Основные задачи статики

Содержание статики абсолютно твердого тела составляют две основные задачи:

1. Задача о приведении сил: как данную систему сил заменить другой, в частности наиболее простой, ей эквивалентной.

2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой.

Первая основная задача имеет важное значение не только в статике, но и в динамике.

Вторая задача часто ставится в тех случаях, когда равновесие заведомо имеет место. Например, когда заранее известно, что тело находится в равновесии, которое обеспечивается связями, наложенными на тело. При этом условия равновесия устанавливают зависимость между всеми силами, приложенными к телу; во многих случаях с помощью этих условий удается определить опорные реакции. Хотя этим не ограничивается сфера интересов статики, нужно иметь в виду, что определение реакций связей (внешних и внутренних) необходимо для последующего расчета прочности конструкции.

В более общем случае, когда рассматривается система тел, имеющих возможность перемещаться друг относительно друга, одной из основных задач статики является задача определения возможных положений равновесия. Эти задачи рассматриваются в аналитической статике.

Глава II. Система сходящихся сил

2.1. Приведение системы сходящихся сил к равнодействующей

Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Простейший пример трех сил был рассмотрен в главе I. Здесь рассматривается общий случай произвольного числа сил, образующих систему.

Существует немало практических задач, которые требуют исследования систем сходящихся сил; в частности, они возникают при расчетах шарнирно-стержневых систем (ферм). Кроме того, изучение системы сходящихся сил необходимо для дальнейших обобщений, относящихся к произвольной системе сил.

Прежде всего докажем теорему:

Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия.

Пусть задана система сходящихся сил F₁, F₂, F₃,…,F_n, приложенных к абсолютно твердому телу. Согласно следствию из аксиомы 1 перенесем точки приложения сил по линии их действия в точку пересечения этих линий. Таким образом, мы получаем систему сил, приложенных к одной точке. Она эквивалентна исходной системе сходящихся сил. Складывая теперь силы F₁ и F₂, на основании аксиомы 3 получим их равнодействующую:

R₂ = F₁ + F₂.

Индекс в обозначении равнодействующей соответствует номеру добавляемой силы F₂. Затем, сложив силу R₂ с силой F₃, найдем

R₃ = R₂ + F₃ = F₁ + F₂ + F₃.

Сила R₃ является равнодействующей трех сил F₁, F₂, F₃ и равна их сумме. Дойдя, таким образом, до последней силы F_п, получим равнодействующую R всей системы данных сил

R = R_n = F₁ + F₂ + F_n =ΣF_i.

Этим соотношением и доказывается справедливость приведенной теоремы.

Построение равнодействующей может быть упрощено, если вместо параллелограммов построить силовой многоугольник. Пусть, например, система состоит из четырех сил. Если из конца вектора F₁ отложить вектор F₂, то вектор, соединяющий начало О и конец вектора F₂, будет вектором R₂.

Далее отложим вектор F₃, помещая его начало в конец вектора F₂. Тогда мы получим вектор R₃, идущий от точки О к концу вектора F₃. Наконец, точно так же прибавим вектор F₄; при этом получим, что вектор, идущий от начала первого вектора F₁ к концу вектора F₄, является равнодействующей R.

Пространственный многоугольник, который получен указанным образом, называется силовым многоугольником.

На рис. 2.2 показан разомкнутый силовой многоугольник (конец последней силы не совпадает с началом первой силы); равнодействующая R направлена по замыкающей силового многоугольника. Конечно, при практическом построении силового многоугольника промежуточные равнодействующие R₂, R₃ и т.д. строить не нужно.

Е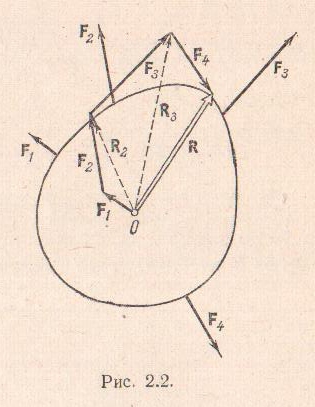 сли для нахождения равнодействующей при помощи силового многоугольника используются правила геометрии или тригонометрии, то такой способ нахождения равнодействующей называется геометрическим способом.

В случае плоской системы сил можно воспользоваться плоским чертежом, откладывая силы в некотором масштабе; равнодействующая определяется непосредственным измерением по чертежу. Такой способ ее нахождения называется графическим.

Наиболее общим способом определения модуля и направления равнодействующей является аналитический способ, который также вытекает из основного соотношения. Поместим, например, начало прямоугольной системы координат в точку пересечения линий действия сил; тогда, пользуясь теоремой, согласно которой проекция векторов на векторную ось равна сумме проекций на ту же ось слагаемых векторов, получим

R_x=F_kx=F_1x+ F_2x+…+F_nx,

R_y=_Fky =F_1y +F_2y+…+F_ny,

R_z=F_kz=F_1z+ F_2z+…+F_nz, (2.2) где F_kx, F_ky, F_kz – проекции силы F_k на указанные оси, а R_x, R_у и R_z – проекции равнодействующей на те же оси.

Итак, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси.

С помощью выражений (2.2) можно найти модуль равнодействующей и ее направлений в прямоугольной системе координат Oxyz.

Так как составляющие равнодействующей R системы сил

R_x= R_xi, R_y= R_yj, R_z= R_zk (2.3) взаимно перпендикулярны, то модуль равнодействующей равен

. (2.4)

Направляющие косинусы равнодействующей соответственно равны

cos(x, R)=R_x/R, cos(y, R)=R_y/R, cos(z, R)=R_z/R. (2.5)

В частном случае, когда все силы расположены в одной плоскости, удобно выбрать систему координат Oxy в плоскости расположения сил. Тогда проекции всех сил на ось z равны нулю и вместо формул (2.2), (2.4) и (2.5) будем иметь

R_x=F_kx=F_1x+ F_2x+…+F_nx,

R_y=_Fky =F_1y +F_2y+…+F_ny, (2.6)

, (2.7)

cos(x, R)=R_x/R, cos(y, R)=R_y/R. (2.8)