
- •Учебное пособие
- •На учебное пособие по дисциплине "общая теория статистики", разработанное к.Э.Н. Юрченко ю.Ю. Для студентов экономических специальностей ДонДуэт
- •Ст. Преподаватель
- •1.1. Статистика как наука
- •1.2. Предмет статистики. Понятия и категории статистической науки
- •1.3. Методология статистики. Стадии статистического исследования
- •1.4. Задачи статистики на современном этапе.
- •1.5. Статистические науки.
- •Статистическая наука
- •Разрабатывает общие принципы и методы статистического исследования общественных явлений, наиболее общие категории (показатели) статистики
- •Контрольные вопросы к теме
- •Общая теория статистики:
- •Разрабатывает общие принципы и методы статистического исследования общественных явлений, наиболее общие категории (показатели) статистики.
- •Разрабатывает общие принципы и методы статистического исследования общественных явлений, наиболее общие категории (показатели) статистики
- •2.1.Статистическое наблюдение - первый этап статистического исследования
- •2.2. Формы статистического наблюдения
- •2.3. Виды статистического наблюдения и способы его проведения
- •Контрольные вопросы к теме
- •3.1. Статистическая сводка - второй этап статистического исследования. Виды группировок
- •3.2. Ряды распределения, их виды и графическое изображение
- •3.3.Статистические таблицы.
- •Из истории
- •Правила составления статистических таблиц
- •Контрольные вопросы к теме
- •Сводка и группировка статистических материалов. Статистические таблицы.
- •4.1.Сущность и значение обобщающих показателей в статистике
- •Обобщающие показатели
- •Абсолютные величины
- •От способа исчисления
- •По признаку времени
- •4.2. Виды абсолютных величин
- •4.3. Виды относительных величин и формы их выражения
- •От способа исчисления
- •По признаку времени
- •5.1. Средняя - ее сущность и определение.
- •5.2. Виды средних величин
- •5.3.Средняя арифметическая
- •5.4. Средняя гармоническая
- •5.5. Мода
- •5.6. Медиана
- •5.7. Средняя альтернативного признака.
- •Опорный конспект с редние величины.
- •6.1. Сущность вариации признака в статистической совокупности
- •6.2. Показатели вариации
- •Дисперсия альтернативного признака.
- •Контрольные вопросы к теме
- •Показатели вариации.
- •7.1. Понятие о выборочном наблюдении, его преимущества
- •7.2. Ошибки выборки
- •Контрольные вопросы к теме
- •По формуле рассчитывают:
- •Выборочное наблюдение является:
- •Формула - это:
- •Опорный конспект в ыборочное наблюдение.
- •8.1. Ряды динамики и их виды
- •8.2. Средний уровень ряда динамики
- •8.3. Важнейшие показатели динамики
- •Темпы роста.
- •Общий вид формулы расчета коэффициента роста:
- •Абсолютное содержание одного процента прироста.
- •Средний коэффициент роста,
- •Р яды динамики.
- •9.1. Сущность индексов, их виды
- •9.2. Индивидуальные индексы
- •9.3. Агрегатные (общие) индексы
- •9.4. Расчет влияния факторов на результативный показатель
- •9.5. Средние из индивидуальных индексов
- •9.6. Индексы средних величин
- •9.7. Цепные и базисные индексы
- •И ндексный метод в статистических исследованиях.
- •10.1. Сущность и виды взаимосвязей из истории
- •10.2. Балансовые приемы анализа взаимосвязей
- •10.3. Факторные взаимосвязи
- •10.4.Роль предварительного теоретического анализа
- •10.5. Однофазный корелляционно-регрессионный анализ
- •Функциональные связи характеризуются:
- •Уравнение является:
- •Средняя ошибка аппроксимации характеризует:
- •Статистическое изучение связи между признаками.
- •Содержание
Темпы роста.
Как и абсолютные изменения, темпы роста являются относительными величинами, бывают цепными и базисными и характеризуют изменение явления во времени. В отличие от абсолютных приростов, темпы роста показывают не на сколько выросло или снизилось изучаемое явление, а во сколько раз оно изменилось. Рассчитывается по аналогии с абсолютными изменениями, только вместо знака «-» знак (/). Единицы измерения - %.
Общий вид формулы расчета темпов роста цепных:
![]()
базисных:
![]() .
.
2.1. Темпы роста цепные показывают, сколько в процентном соотношении составляет уровень отчетного периода по сравнению с предыдущим.
![]() =
=
![]() *100=123,03 %
*100=123,03 %
![]() =
=
![]() *100=111,51%
*100=111,51%
![]() =
=
![]() *100 = 111,36%
*100 = 111,36%
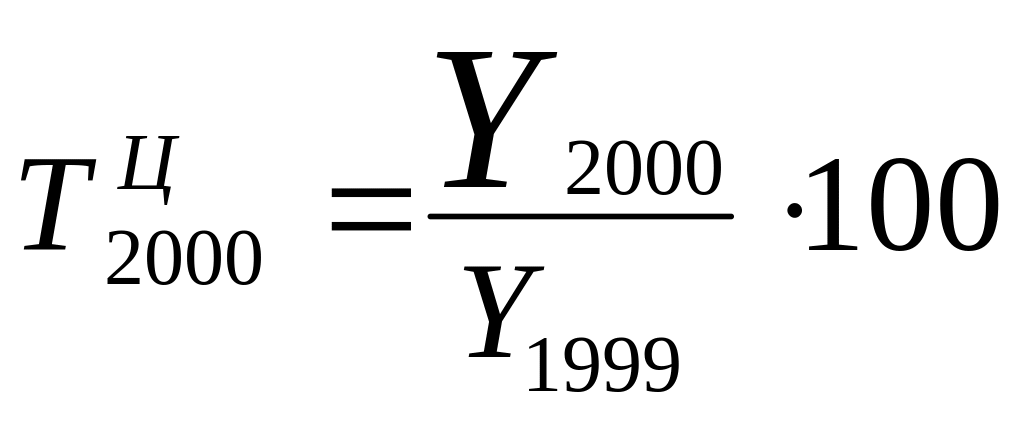 =
=
=
=![]() *100
=140,76%
*100
=140,76%
![]() ,
к примеру, показывает, что по сравнению
с 1998 уровень расходов населения составил
111,51%.
,
к примеру, показывает, что по сравнению
с 1998 уровень расходов населения составил
111,51%.
![]() =140,76%
означает, что уровень потребления в
2000 году по сравнению с 1999 годом составил
140,76%.
=140,76%
означает, что уровень потребления в
2000 году по сравнению с 1999 годом составил
140,76%.
2.2. Темпы роста базисные показывают, сколько в процентном соотношении составляет уровень отчетного периода по сравнению с базисным.
![]() =
*100=123,03 %
=
*100=123,03 %
![]() =
=
![]() *100=152,76%
*100=152,76%
 =
=![]() *100=
137,00%
*100=
137,00%
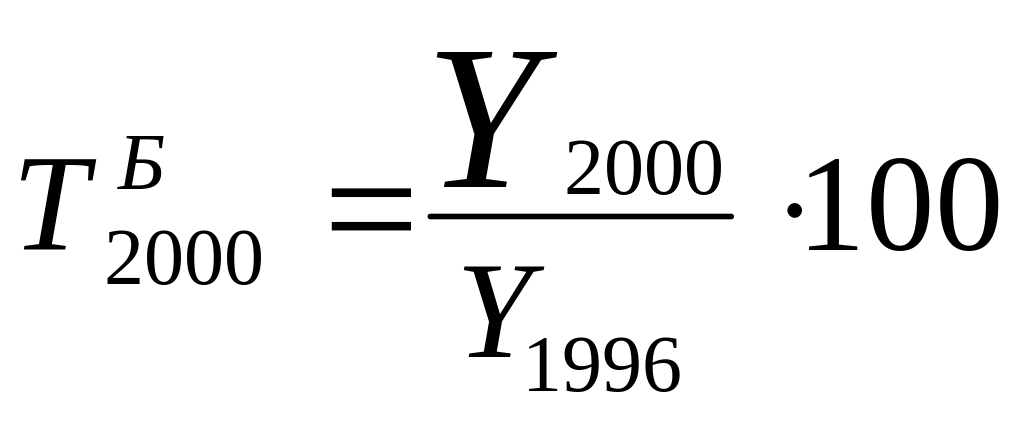 =
=
=
=![]() *100
=215,03%
*100
=215,03%
Так, рассчитанный нами показывает, что уровень расходов в 1999 году по отношению к базисному составил 152,76%, а в 2000 году по сравнению с 1996 годом – 215,03%.
Темп прироста показывает, на сколько процентов изменилось изучаемое явление.
Общая формула расчета темпа прироста: t=T-100%.
Темпы прироста также бывают цепными и базисными.
tц=Tц-100%. tб=Tб-100%.
![]() 123,03%-100%=23,03%
123,03%-100%=23,03%
![]() 111,51%-100%=11,51%
111,51%-100%=11,51%
![]() 111,36%-100%=11,36%
111,36%-100%=11,36%
![]() 140,76%-100%=40,76%
140,76%-100%=40,76%
Так, темп прироста цепной за 1999года, равный 11,51% показывает, что расходы населения в 1999 году выше, чем в 1998 на 11,51%.
![]() 123,03%-100%=23,03%
123,03%-100%=23,03%
![]() 152,76%-100%=52,76%
152,76%-100%=52,76%
![]() 137,00%-100%=37,00%
137,00%-100%=37,00%
![]() 215,03%-100%=115,03%
215,03%-100%=115,03%
Темп роста, не переведенный в проценты, является коэффициентом роста.
Общий вид формулы расчета коэффициента роста:
![]() цепных
цепных
![]() .
базисных
.
базисных
или
![]()
![]()
Коэффициент роста характеризует изменение показателя в разах (а не в %).
Произведение
цепных коэффициентов роста равно
конечному базисному
![]()
По данным примера: 1,23031,11361,11511,4076=2,1503.
Взаимосвязь цепных и базисных коэффициентов роста (при условии, что базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики):
произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период;
если разделить базисный коэффициент на предыдущий базисный, то получится текущий цепной коэффициент;
если базисный коэффициент текущего периода разделить на цепной коэффициент этого же периода, получится предыдущий базисный коэффициент.
Абсолютное содержание одного процента прироста.
Рассчитывается показатель как отношение абсолютного прироста к темпу прироста (рассчитывается только цепной показатель) и показывает, какое абсолютное значение скрывается за одним процентом прироста.
Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста.
Формула расчета следующая:

Преобразовав формулу получаем:
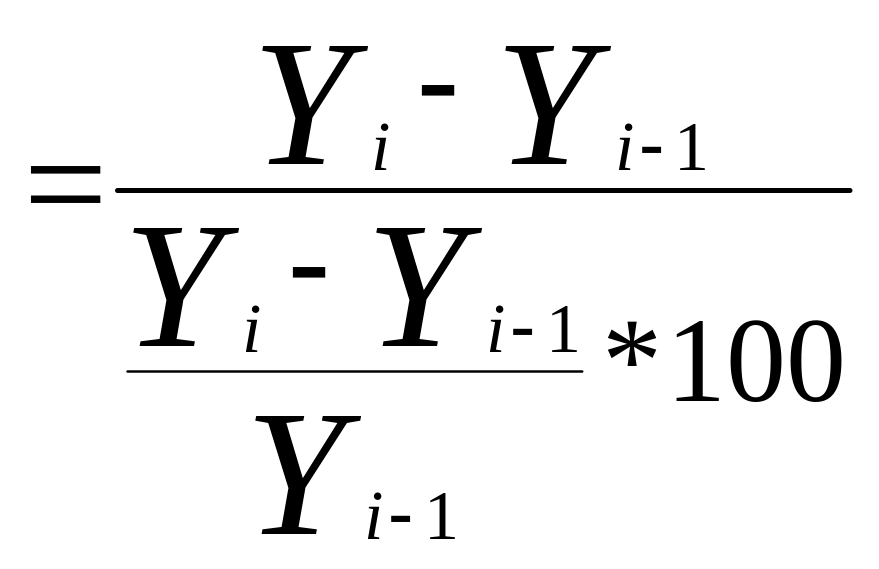 =
=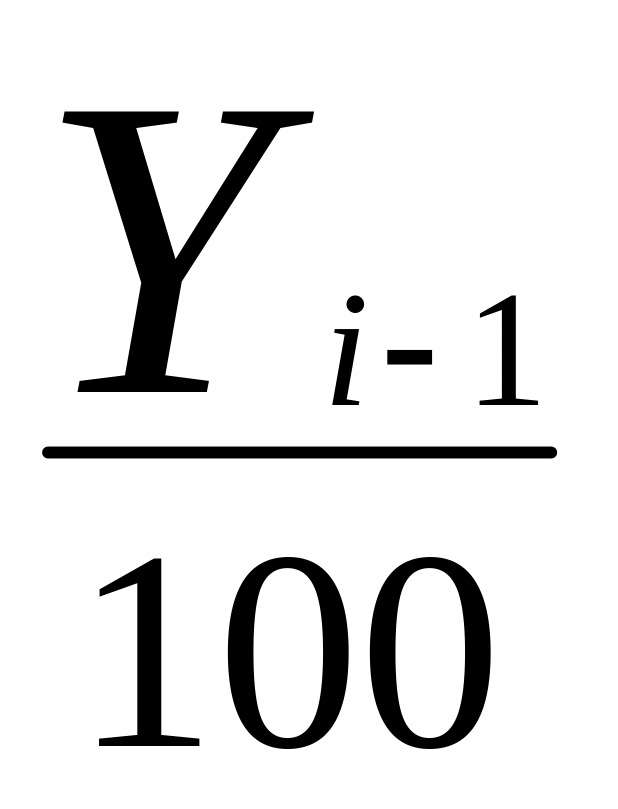 =0,01
=0,01![]()
Таким образом, мы вывели, что абсолютное значение 1% прироста равно сотой части предыдущего уровня.
Годы |
Ед. изм. |
1996 |
1997 |
1998 |
1999 |
2000 |
Показатели |
||||||
Денежные расходы |
млн. грн. |
38961,00 |
47933,00 |
53376,00 |
59518,00 |
83777,00 |
|
млн. грн. |
|
8972,00 |
5443,00 |
6142,00 |
24259,00 |
Темп прироста цепной |
% |
|
23,03 |
11,36 |
11,51 |
40,76 |
Абсолютное значение 1% прироста |
млн. грн. |
|
389,61 |
479,33 |
533,76 |
595,18 |
В нашем примере абсолютное значение 1% прироста с 1996 по 2000годы возрастало.
Обобщающими показателями скорости изменения уровней во времени являются:



 Абсолютные
изменения (цепные)
Абсолютные
изменения (цепные)