7.2. Ошибки выборки

Совокупность из которой производится отбор, называется генеральной, (N - численность генеральной совокупности) а все ее обобщающие показатели, генеральными.

Совокупность отобранных единиц – выборочной совокупностью, все ее обобщающие показатели – выборочными, число отобранных единиц – n.

Основная задача выборочного наблюдения – на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности.

Вся изучаемая совокупность явлений (единиц) называется генеральной совокупностью (N - численность генеральной совокупности). Часть единиц, отобранная на основе разработанных принципов из генеральной совокупности, называется выборочной совокупностью (n).

Показатели	Обозначение показателей в
	Генеральной совокупности	Выборочной совокупности
Численность единиц совокупности	N	n
Среднее значение признака
Дисперсия	2	S2
Среднее квадратическое отклонение		S
Доля	P	W

Средняя ( ) и доля ( ) генеральной совокупности будут несколько отличны от средней ( ) и доли ( ) в выборочной совокупности на некоторую величину .: или ; или .

Интервал называется доверительным.

Величину отклонения или среднюю ошибку выборки можно определить по формулам:

, ,

где , - средняя ошибка выборочной средней и выборочной доли соответственно.

Показатели  и р генеральной совокупности нам неизвестны. Но в теории вероятностей доказано, что в случаях, когда объем выборки превышает 30, можно принять, что , таким образом, в практических расчетах средних ошибок выборки можно использовать формулы:

,

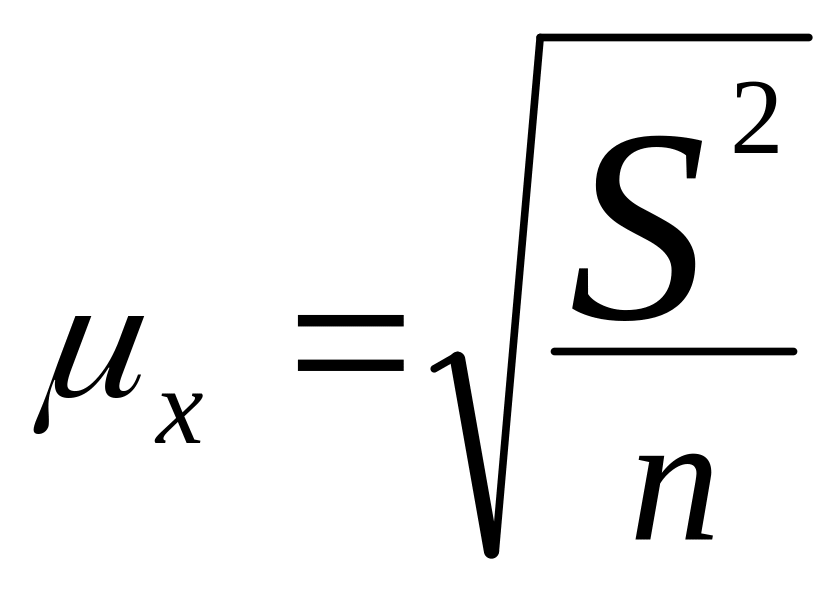Чтобы определить уровень среднедушевого дохода в городе было обследовано 500 семей. Средний уровень составил 150 грн., дисперсия выборки – 1120, n=500, =150, S²=1120

Исчислим среднюю ошибку выборки: = =1,5,

Это значит, что среднедушевой доход населения города находится в пределах от 148,5 грн. (150-1,5) до 151,5 грн. (150+1,5).

Однако ошибка выборки имеют определенную вероятность возникновения. Это означает, что средняя в целом по генеральной совокупности, может находиться в указанных пределах, а может и не находиться. Доказано, что степень вероятности отклонения генеральных характеристик от выборочных – постоянная величина 0,683. Это значит, что в 683 случаях из 1000, средняя генеральной совокупности (х) не выйдет за пределы +- . А в остальных 317 случаях может отличаться от на величину, большую чем .

В нашем примере в 683 случаях среднедушевой доход лежит в пределах 148,5 < 150 < 151,5. В 317 случаях - может выйти за указанные пределы.

Если мы хотим повысить вероятность утверждения, можно расширить пределы, увеличив в некоторое количество раз. С увеличением в - t раз, увеличивается степень вероятности наших утверждений. Приведем некоторые известные нам из курса «Математическая статистика» значения вероятностей при разной величине так называемого коэффициента доверия - t.

Значения вероятностей соответствующие коэффициенту доверия.

t	вероятность	T	вероятность	t	вероятность
1,0	0,6827	2	0,9545	2,7	0,9931
1,1	0,7287	2,5	0,9876	2,8	0,9949
1,7	0,9109	2,58	0,9900	3,0	0,9973
1,96	0,9500	2,6	0,9907	3,28	0,9990

Выделенные в таблице коэффициенты доверия с соответствующей степенью вероятности часто используются на практике.

Расширив в рассматриваемом примере пределы отклонений в 3,28 раз, получим следующий доверительный интервал:

150-3,281,5 150 150+3,281,5

145,08 150 159,92

т.е. в 999 случаях из тысячи средушевой доход будет находиться в указанных пределах.

С учетом коэффициента доверия t, доверительный интервал преображается и выглядит следующим образом:

Величина обозначается  (греческая буква “дельта”) и носит название – предельная ошибка выборки.

Формулы доверительных интервалов имеют вид:

; ,

Поступила на склад партия товаров в количестве 20000 единиц. Выборочному обследованию подвергли качество 200 единиц. Из них 12 – бракованные. Какова доля брака всей продукции?

Мы имеем n=200, w=12/200=0,06. Доля брака в выборочной совокупности – 0,06 или на каждые 100 изделий – 6 бракованных. Для определения доли бракованной продукции в генеральной совокупности используем формулу = = = =0,0158

Мы получили ; или 0,06-0,0158 0,06+0,0158.

Следовательно, с вероятностью 0,683, можно утверждать, что доля брака во всей продукции находится в пределах от 0,0442(0,06-0,0158) до 0,0758 (0,06+0,0158) или в 683 случаях из 1000 процент бракованных изделий в генеральной совокупности будет составлять в среднем от 4,4% до 7,6%.

Приведенные формулы для определения величины ошибки выборки дают возможность рассчитывать, какую необходимо взять численность выборки, чтобы ошибка выборки не превышала определенных заданных размеров.

Если , то 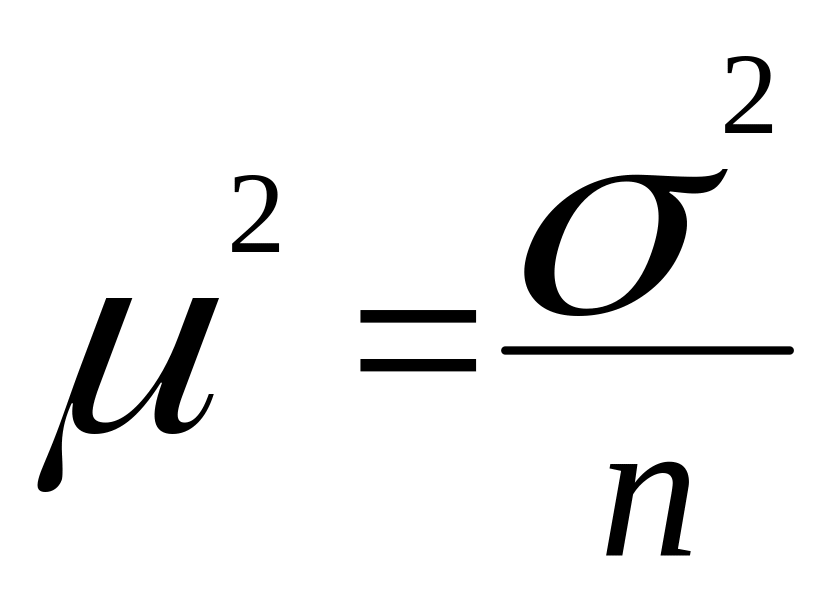, а n= ,

т.е. необходимая численность выборки при измерении средней равна среднему квадрату отклонений, деленному на квадрат допустимой ошибки выборки.

Если в формулу ввести коэффициент t, то она примет такой вид:

n=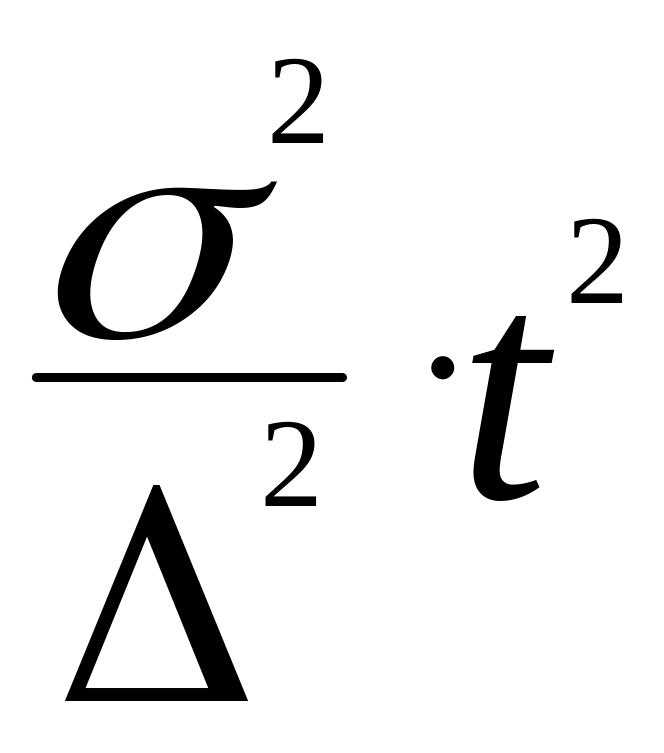

При выборочном измерении доли признака средняя ошибка выборки определяется по формуле

, откуда n= ,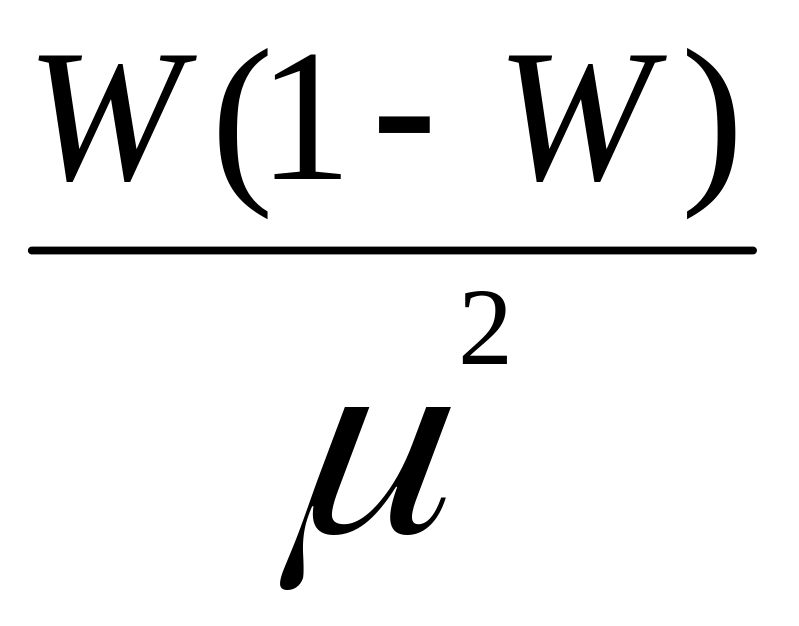

т.е. необходимая численность выборки равна доле, умноженной на дополнение ее до единицы и деленной на квадрат заданной точности.

Если в формулу ввести коэффициент t, то она примет такой вид:

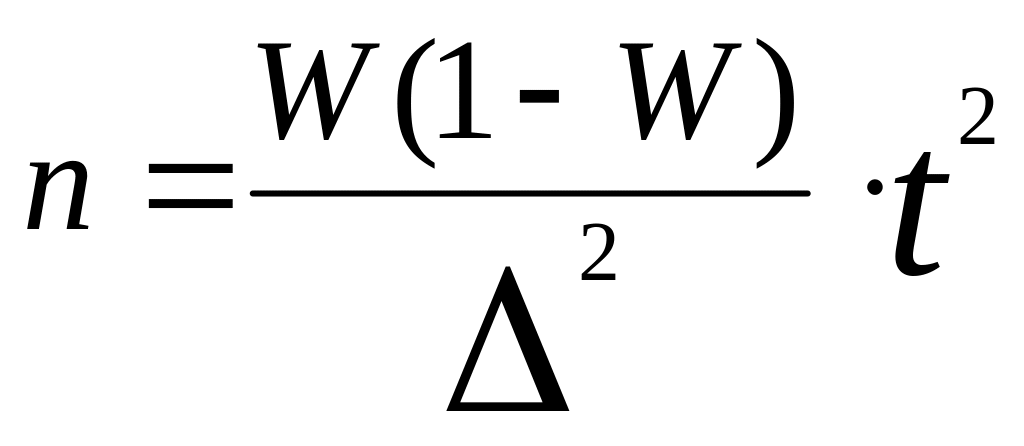
Чтобы определить средний размер платы за 1м² арендуемой площади, обследовали 40 предприятий, рассчитан средний размер арендной платы – 30грн. за 1м². Дисперсия составила – 60. Определить численность выборки, если с вероятностью 0,95 гарантировать, что размер ошибки выборки не будет превышать 1 грн.

Решение:

Из условия мы имеем - 60, =1. В таблице … находим соответствующий вероятности 0,95 коэффициент доверия t=1,96. Для решения воспользуемся формулой:

n= = =230,4 предприятия.

Из 32 опрошенных предпринимателей высшее образование имеют – 11. Какова должна быть численность выборки, чтобы с вероятностью 0,99 предельная ошибка выборки не превышала 5% (т.е.0,05)

Решение:

Для расчета используем формулу:

По данным таблицы … находим, что вероятности 0,99 соответствует коэффициент доверия t=2.58, W=11/32,=0,01

= =584 человека.

7.3. Способы отбора единиц,

подлежащих выборочному наблюдению

Результаты выборочного наблюдения в значительной степени определяются правильностью отбора отдельных единиц для последующего их описания. Для получения репрезентативной выборки применяют различные способы, использование которых зависит от характера исследуемых явлений. Различают четыре вида отбора: собственно-случайный, типический, механический и серийный.

При использовании собственно-случайного отбора единица попадает в выборку совершенно случайно: по жребию, лотерее, таблицам случайных чисел.

Типический отбор заключается в том, что все единицы генеральной совокупности предварительно распределяются на отдельные типичные группы по существенному для исследований признаку. В результате выборочная совокупность точнее воспроизводит генеральную совокупность.

Сущность механического отбора заключается в том, что единицы генеральной совокупности располагаются в каком-либо порядке (в хронологическом порядке, по географическому положению, по возрастанию или убыванию какого либо признака), а затем выбирают каждую 3, 10, 100, 257 ... единицу исходя из необходимого количества единиц в выборочной совокупности.

Сущность серийного отбора заключается в том, что отбору подлежат не отдельные единицы генеральной совокупности, а целые серии таких единиц.

Каждый из способов имеет свои особенности, поэтому их часто сочетают. Наиболее точным является типический отбор, а наименее точным, но наименее трудоемким является серийный отбор.

Одной из наиболее важных и ответственных задач при организации и проведении выборочного наблюдения является установление необходимой численности выборки (выборочной совокупности). Расчет основывается на формулах предельной ошибки выборки.

- для повторного способа:

- для вариационного признака (х), аналогично

- для альтернативного признака (р).

Для бесповторного способа подобные преобразования дадут такие формулы:

- для вариационного признака (х);

- для альтернативного признака (р).

После отбора единиц производится проверка репрезентативности, то есть устанавливается, на какую величину значения основных признаков выборочной совокупности отклоняются от значения этих признаков в генеральной совокупности. В качестве показателя репрезентативности выборки можно определить соотношение для известных данных. Выборка считается репрезентативной, если указанное отношение находится в пределах от 95% до 105%. Если указанные пределы отличаются, то отбор повторяется, пока репрезентативность выборочной совокупности не станет удовлетворительной.