6.2. Показатели вариации
Наиболее
простым показателем вариации является
размах
вариации
.
Для варианта «А»: 8-2=6 Для варианта «Б»: 15-1=14.
Размах
вариации улавливает только крайние
отклонения, но представляет интерес
отклонение каждой варианты от средней
или «линейное отклонение от средней»:
По
нижеследующим данным произведем расчет
показателей вариации приведенной
совокупности. Воспользовавшись формулой
для расчета средней арифметической
простой, находим среднее значение равное
16 (
).
Во второй колонке – отклонения каждой варианты от среднего значения.
|
x |
x- |
|x- | |
(x- )2 |
|
10 |
-6 |
6 |
36 |
|
12 |
-4 |
4 |
16 |
|
16 |
0 |
0 |
0 |
|
20 |
4 |
4 |
16 |
|
22 |
6 |
6 |
36 |
Итого: |
80 |
0 |
20 |
104 |
Чтобы
найти среднее линейное отклонение
используем среднюю арифметическую, но
поскольку
(по свойству средней), следует все
отклонения взять по модулю. Теперь,
используя среднюю арифметическую
находим среднее линейное отклонение
простое
,
где n-количество вариант в совокупности.
В нашем
примере среднее линейное отклонение
равняется 4 (
).
Но этот показатель в качестве меры
вариации в статистике применяют редко.
Чаще отклонения от средней возводят в
квадрат и из суммы квадратов отклонений
исчисляют среднюю величину. Этот
показатель называется дисперсией:
.
В нашем
примере
20,8.
Если извлечь корень из дисперсии, мы получим новый показатель – среднее квадратическое отклонение:
,
или
Дисперсия
и среднее квадратическое отклонение
являются общепринятыми мерами вариации
признака. Их широко применяют в статистике.
Среднее квадратическое отклонение
имеет те же единицы измерения, что и
варианта. При сравнении вариации разных
признаков или одного признака в разных
совокупностях используется коэффициент
вариации:
,
обычно выражается в процентах.
В
рассматриваемом нами примере
4,56;
=28,5%.
Если мы имеем вариационный ряд распределения, то для расчета показателей вариации используем следующие формулы:
-
среднее линейное отклонение взвешенное.
-
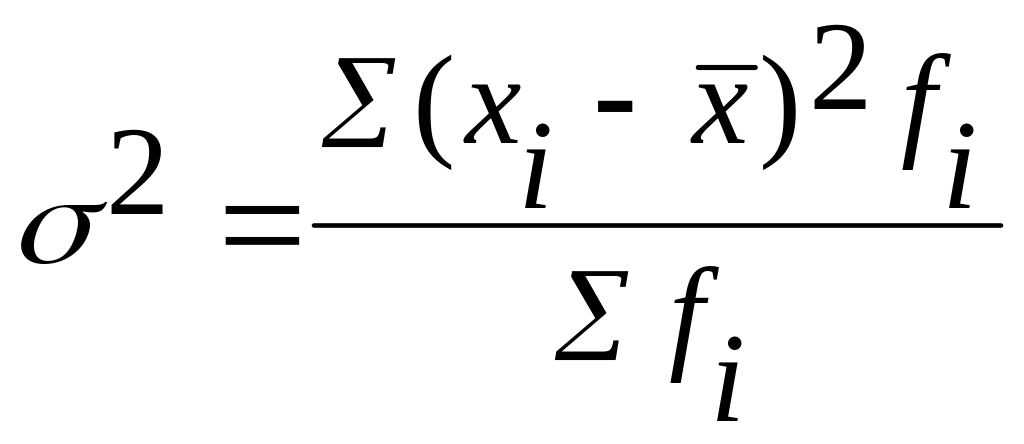дисперсия взвешенная
-
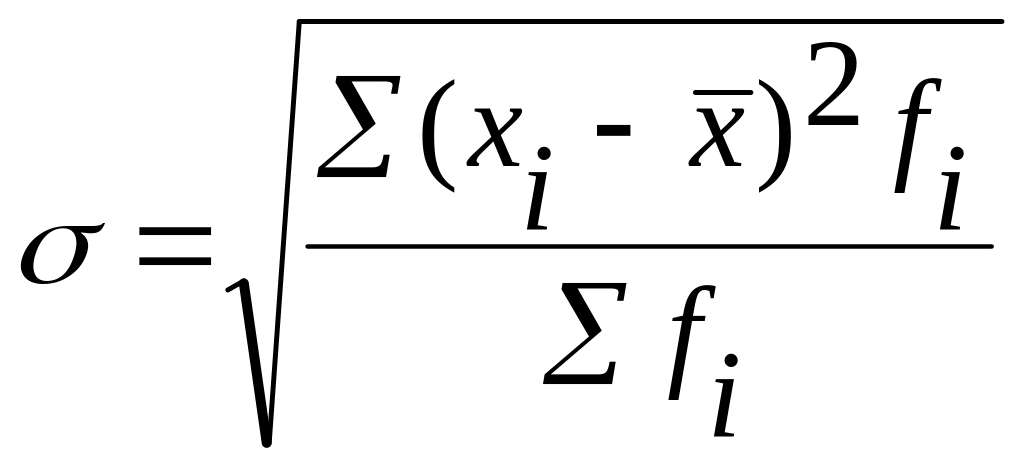среднее квадратическое отклонение
взвешенное
Ниже приведен пример расчета показателей вариации в вариационном ряду распределения.
x |
f |
x·f |
x- |
(x- )·f |
|x- |·f |
(x- )2 |
(x- )2·f |
2 |
3 |
6 |
-4 |
-12 |
12 |
16,2 |
48,5 |
4 |
31 |
124 |
-2 |
-63 |
63 |
4,1 |
126,4 |
6 |
32 |
192 |
0 |
-1 |
1 |
0 |
0 |
8 |
38 |
304 |
2 |
75 |
75 |
3,9 |
149,1 |
Итого: |
104 |
326 |
х |
0 |
151 |
х |
324,0 |
Результаты расчетов следующие:
Среднее значение – 6,02
Среднее линейное отклонение – 1,45
Дисперсия – 3,12
Среднее квадратическое отклонение – 1,76
Коэффициент вариации – 29,32%.