49. Решение матричных игр 2*2

Игра 2×2 явл. Наиболее простым случаем конечных матричных игр. В этой игре каждый из игроков обладает только двумя стратегиями. Если игра 2×2 имеет седловую точку, то ее решение очевидно. Рассмотрим игру

В1 В2

А1 а11 а12

А2 а21 а22

Предположим, что игра не имеет седловой точки, т. Е. α<β. Требуется найти оптимальную смешанную стратегию игроков p*=(p1, p2) и q*=(q1, q2), а также цену игры v.

Очевидно, что в игре 2×2, не имеющей седловую точку, обе стратегии игроков явл. Активными. Поэтому, если игрок А, будет применять свою оптим. смешанную стратегию, то неизменно от действий игрока В, выигрыш его будет = цене игры v.

Игрок А будет применять стратегию А1 с вероятностью p1 и стратегию А2 с вер-тью p2. Если игрок В отвечает своей стратегией В1, то выигрыш игрока А определяется из уравнения: [а11*р1+а21*р2=v]

Если же игрок В будет применять стратегию В2, то выигрыш игр. А не изменится и определ. Равенством: а12*р1+а22*р2=v

Учитывая условие р1+р2=1 получим систему 3х уравнений с 3мя неизвестными

a11р1+а21р2=v

a12p1+a22p2=v

P1+p2=1

Решив эту систему найдем оптимальное решение для игрока А: р*=(р1, з2) и цену игры v.

Аналогично определяется оптимальная стратегия игрока В из системы уравнений:

a11q1+a21q2=v

a21q1+a22q2=v

q1+q2=1

Решив эту систему найдем оптимальное решение для игрока В: q*=(q1,q2)

50. Сведение ми к злп

Рассм. матричную игру с платежной матрицей:

Обозначим через р*=(р1,р2,р3) и q*=(q1,q2,q3) оптимальные стратегии игроков А и В.

Стратегия р* игрока А гарантирует ему выигрыш не меньше цены игры, независимо от выбора стратегии Вj игроком В.

Система уравнений (1)

Где р1+р2+р3=1, pi≥0, i=1,3

Аналогично для игрока В. Стратегия q* игрока В гарантирует ему проигрыш не больше цены игры v, независимо от выбора стратегии Аi игроком А.

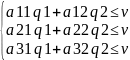(2)

Q1+q2=1, qj≥0, j=1,2

Т.к. элементы платежной матрицы всегда можно сделать положительными, то и цена игры будет больше 0.

Преобразуем системы 1 и 2 , разделив обе части каждого неравенства на положительное число v, и введем новое обозначение: xi=pi/v≥0, yj=qj/v≥0, i=1,3, j=1,2

Получим (3)

X1+x2+x3=1/v, xi≥0, i=1,3

(4)

Y1+y1=1/v, yj≥0, j=1,2

Т.к. игрок А стремится максимизировать цену игры, то обратная величина 1/v будетминимизироваться, поэтому оптимальная стратегия игрока А определяется из ЗЛП следующего вида:

Z(x)=x1+x2+x3→min

При ограничениях (3)

Для игрока В: f(y)=y1+y2→max при ограничениях (4)

Решив пару двойственных задач графическими или симплекс-методом далее опред. решение матричной игры.

V=1/ , pi=xi*/ =xi*v, qj= yi*/ =yj*v

Алгоритм решения матричной игры:

1.Упрощаем платежную матрицу

2.Проверяем имеет ли игра решение в чистых стратегиях

3. если решение находится в смешанных стратегиях, то решаем либо сведением к системе линейных алгебраических уравнений (2×2), либо сведением к ЗЛП.

51.Статистические игры. Основные понятия.

Под стат. игрой или игрой с природой мы будем понимать парную матричную игру, в кот. 1 игрок заинтересован в наиболее выгодном для себя исходе игры, а второй игрок-природа (П), совершенно безразличен к результату игры. Предположим, что в игре с природой сознательный игрок А м. Использовать m чистых стратегий: m: A₁,A₂,…..A_m, а 2 игрок П м. реализовать n различных состояний n: П₁,П₂…П_n. Игроку А м.б. известны вероятности q₁,q₂….q_n, с кот. природа реализует свои состояния, но он может и не знать их. Действуя против природы, игрок А м. реализовать как свои чистые стратегии A_i, так и смешанные. Если игрок А в состоянии оценить некоторой величиной а_ij последствия применения каждой своей чистой стратегии A_i при любом состоянии природы П_j, то игру м. задать матрицей.

А=

Игры с природой явл-ся частным случаем матр. игр.

При упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, т.к. она м. реализовать любое состояние независимо от того выгодно оно или нет. Решение достаточно найти только для игрока А поскольку природа наши рекомендации воспринять не может. Смешанные стратегии приобретают смысл только при многократном повторении игры.

Решение статистич. игры: 1) упростить платежную матрицу. Отбрасывать стратегии природы нельзя (столбики на месте) 2) оценить выигрыш при различных игровых ситуациях(критерий Байеса, Вальда, Гурвица, Сэвиджа. 3) построить и исследовать матрицу риска 4)сделать вывод о выборе наилучшей стратегии.

критерием Байеса:

1. Критерий, основанный на известных вероятностях условий. Пусть известны вероятности q_j состояний природы П , j=1;n.Тогда пользуемся критерием Байеса, в соответствии с кот. Оптимальная считается чистая стратегия A , при которой максимизируется средний выигрыш

= i=1;n

игрока А, т.е. определяется величина:

=

Лапласа:

2. Если объективные оценки состояния природы получить невозможно, но вероятности природы могут быть оценены субъективно на основе принципа недостаточного основания Лапласа, согласно которому все состояния природы полагаются равновероятностными, т.е.

q₁=q₂=…….=q_n= и оптимальной считают стратегию А_i, обеспечивающую максимальное среднее значение выигрыша

=

Если вероятности q_j состояний природы неизвестны и нельзя сделать о них никаких предположений, то пользуемся критериями Вальда, Гурвица, Сэвиджа.