8. Пространственное вращение вокруг произвольной оси.
Пространственное вращение вокруг произвольной оси. Данную операцию можно в какой-то мере считать универсальной и на ее базе реализовывать все остальные операции в пространстве. Так эта операция не относится к элементарным, ее следует разложить на простейшие. Из них в данном случае потребуются операции переноса и вращения вокруг осей координат. Для того чтобы свести операцию вращения вокруг произвольной оси к эти операциям, необходимо выполнить следующие действия:
• перенести исходную ось вращения таким образом, чтобы она проходила через начало системы координат.
• повернуть перемещаемую ось до совпадения с одной из координатных плоскостей
• в пределах выбранной координатной плоскости осуществить плоский поворот до совпадения с одной из координатных осей
• теперь можно выполнить заданный поворот вокруг оси, которая совмещена с одной из осей координат
• повторение действий в обратном порядке
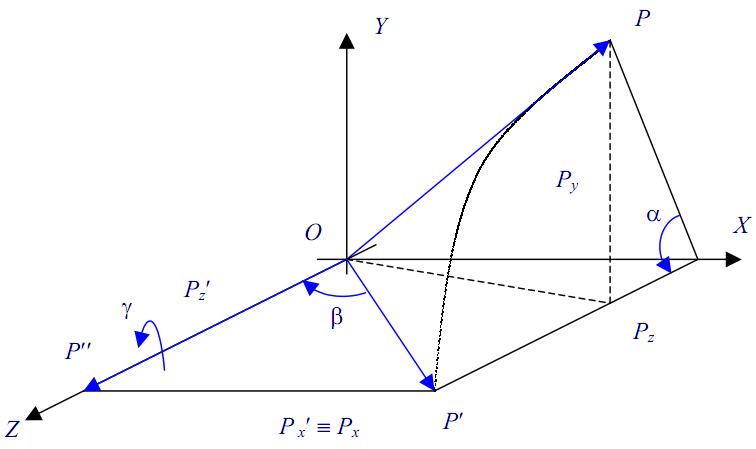
Рассмотрим поворот на угол γ вокруг произвольной оси. Для этого необходимо выполнить следующие семь шагов:
1. Перенос оси вращения в начало системы координат.
2. Поворот на угол α относительно оси ОХ до пересечения с плоскостью XOZ
3. Поворот на угол β в плоскости XOZ до совмещения с осью OZ
4. Поворот на угол γ вокруг оси OZ
5. Поворот на угол - β вокруг OY
6. Поворот на угол - α вокруг ОХ
7. Перенос оси вращения на прежнее место
Рассмотрим математическое описание данных действий в матричном виде. Будем описывать все производимые действия в виде вложенных преобразований конгруэнтности.
1. Преобразование переноса (прямое и обратное):
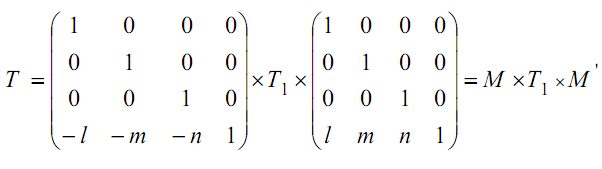
2. Поворот на угол α относительно ОХ:
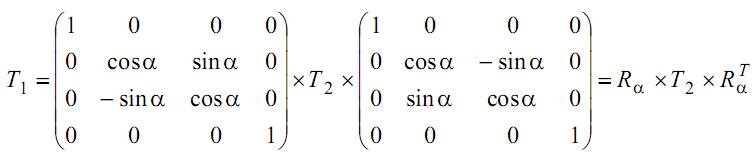
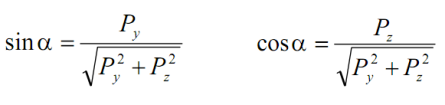
3. Поворот на угол β относительно OY до совмещения с осью OZ :
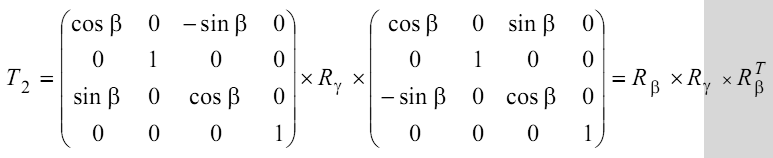
4. Поворот на угол γ :
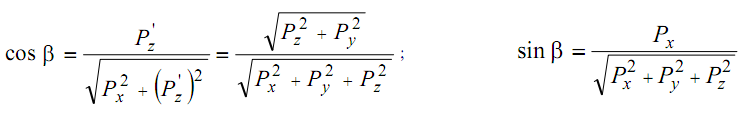
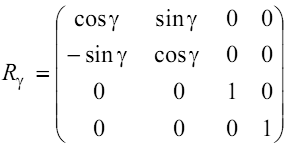
Полное преобразование, описывающее поворот в пространстве вокруг произвольной оси:
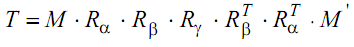
Конец 8 вопроса.
9. Классификация плоских проекций.
Перед разработчиками информационных систем, использующих средства пространственного моделирования, встает задача преобразования трехмерных объектов и сцен, состоящих из них, для представления на плоских поверхностях устройств изображения, т.е. задача перехода из трехмерного пространства на плоскость. Процесс перехода с трехмерного пространства на плоскость не является однозначным, т.е. для одного трехмерного объекта возможно множество двумерных проекций. В начертательной геометрии и черчении различают следующие проекции:
• перспективная, которая находит широкое применение в живописи, архитектуре
• параллельная, использующаяся в основном в технических приложениях.
Однако в последнее время и средства технического проектирования стали ориентироваться на более реалистичные перспективные проекции.
При построении перспективной проекции выбирается один или несколько центров проецирования, после чего определяются точки пересечения плоскости проецирования с лучами проецирования – прямыми, исходящими из центра проецирования.
Перспективное (центральное) проецирование можно рассматривать как наиболее общий случай (рис.2.11). Причем его можно разложить на два преобразования:
• перспективное преобразование, осуществляющее переход из двумерного пространства в перспективное
• двумерное проецирование, осуществляющее переход из двумерного пространства в двумерную плоскость
Параллельное проецирование (рис.2.12) можно рассматривать как частный случай перспективного проецирования, при котором центр проецирования удален в бесконечность. При этом лучи проецирования становятся параллельными друг другу.
Параллельная проекция называется аксонометрической в том случае, если линии проецирования перпендикулярны плоскости проецирования. В противном случае проекции называются косоугольными.
В практике технического проектирования наиболее распространены аксонометрические проекции, среди которых различают четыре вида.
1. Прямоугольные (ортогональные) – проекции, у которых плоскости проецирования параллельны координатным плоскостям. Частным случаем ортогональной проекции, при которой плоскости проецирования совпадают с координатными плоскостями, является ортографическая проекция
2. Изометрическая проекция (изометрия) – это проекция, для которой предполагается одинаковое масштабирование по всем трем осям. Следствием этого является равенство всех углов между проекциями координатных осей
3. Диметрическая проекция (диметрия) – проекция, у которой масштаб по одной из осей координат выбран вдвое меньше, чем по двум другим.
4. Триметрическая проекция (триметрия) – не накладывает никаких ограничений на масштабирование осей, следствием чего является произвольное расположение проекций координатных осей на плоскости проецирования.
Конец 9 вопроса.