
- •1. Графические данные и их классификация.
- •2. Алгоритмы компьютерной графики.
- •3. Аппаратные средства компьютерной графики.
- •4. Понятие геометрической машины. Структурная схема графической системы.
- •5. Базовая графическая система (бгс). Gks – международный стандарт на бгс.
- •6. Элементарные (базовые) и комбинированные операции на плоскости.
- •7. Элементарные (базовые) и комбинированные операции в пространстве.
- •8. Пространственное вращение вокруг произвольной оси.
- •9. Классификация плоских проекций.
- •10. Ортографическая проекция
- •11. Геометрические построения в диметрической проекции.
- •12. Геометрические построения в изометрической проекции.
- •13. Косоугольные проекции.
- •14. Виды перспективного проецирования.
- •15. Перспективная одноточечная проекция.
- •16. Перспективная двухточечная проекция.
- •17. Перспективная трехточечная проекция.
- •32. Каркасные модели. Модели твердого тела.
- •33. Параметрическое описание пространственных кривых. Модели кривых линий.
- •34. Представление пространственных кривых в форме Эрмита.
- •35. Представление пространственных кривых в форме Безье.
- •36. Кривые Бернштейна-Безье.
- •37. Представление пространственных кривых в сплайновой форме.
- •44.Колориметрия. Законы Грассмана.
- •45.Табличные и библиотечные форматы представления цвета.
- •46. Базовые цветовые модели, ориентированные на аппаратуру.
- •47.Телевизионные цветовые модели.(yiq и yuv)
- •48.Модели цифровой фотографии
- •49. Художественные цветовые модели, или
- •50.Абстрактные цветовые модели cie xyz и cie l*a*b*.
- •51. Модель освещения, используемая для построения реалистических изображений.
- •52.Модель освещения с учетом микрогеометрии поверхностей объектов.
- •53.Учет коэффициента Френеля в модели освещения с учетом микрогеометрии поверхностей объектов.
- •54.Функция распределения микрограней в модели освещения с учетом микрогеометрии поверхностей объектов.
- •55.Функция ослабления света на микрогранях в модели освещения с учетом микрогеометрии поверхностей объектов.
- •56.Моделирование прозрачности и теней.
- •57.Методы трассировки лучей. Алгоритмы прямого хода луча.
- •58.Методы трассировки лучей. Алгоритмы обратного хода луча.
- •59.Построения реалистических изображений методом излучательности.
- •60.Модель закраски Гуро.
- •61.Модель закраски Фонга.
- •62.Алгоритм отсечения лучей.
- •63.Алгоритм двоичного разбиения пространства (bsp-алгоритм).
- •66. Текстурирование объектов
- •67.Классификация методов сжатия графической информации.
- •68.Метод группового кодирования (rle-алгоритм).
- •69.Методы кодирования строк бит переменной длины. Алгоритм Хаффмена и арифметическое кодирование.
- •70.Алгоритмы сжатия со словарем (lz-алгоритмы).
- •71.Алгоритм сжатия jpeg.
- •72.Алгоритм волнового сжатия (вейвлет-преобразование).
- •73.Фрактальная математика и фрактальное сжатие.
- •75.Форматы представления видеоданных: Microsoft riff avi, mpeg-1,2,4, QuickTime
- •9. Форматы mpeg
- •80. Логические устройства стандартной видеосистемы пк
- •81. Современные режимы работы видеосистем
- •82. Организация взаимодействия в современных видеосистемах пк. Аппаратные интерфейсы
- •83. Графические процессоры ati и nVidia
- •84. Ускорение вычислений при помощи технологий sli и CrossFire
- •18. Виды растровой развертки.
- •19. Алгоритм Брезенхема растровой развертки отрезков прямых.
- •20. Алгоритмы Брезенхема растровой развертки окружностей.
- •21. Построчный алгоритм растровой развертки сплошных областей.
- •22. Алгоритм растровой развертки сплошных областей с затравкой.
- •23. Алгоритм отсечения отрезков на плоскости.
- •24. Алгоритмы отсечения многоугольников на плоскости.
- •25. Алгоритмы отсечения в пространстве изображений
- •26. Алгоритмы отсечения в пространстве объектов
- •27. Алгоритмы сортировки по глубине.
- •28. Простейшие алгоритмы масштабирования растровых изображений.
- •29. Масштабирование растровых изображений с использованием форм Безье и в-сплайнов.
- •30. Алгоритмы фильтрации растровых изображений, базирующиеся на свертке.
- •31. Медианная фильтрация растровых изображений.
- •76. Интерфейс Windows gdi
- •77.Интерфейс Microsoft Windows DirectX.
- •78.Интерфейсы Microsoft Windows DirectDraw и DirectAnimation.
- •78.Интерфейс Microsoft Windows Direct3d.
- •79.Интерфейс по стандарту OpenGl.
28. Простейшие алгоритмы масштабирования растровых изображений.
В современных системах наибольшее распространение получил метод перевыборки. Этот метод является следствием из более общего класса задач геометрической коррекции или, по-другому, восстановления изображения в преобразованных координатах.

Н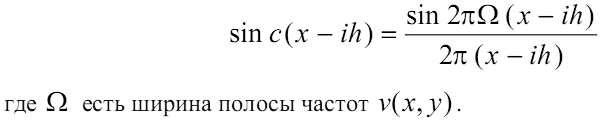 а
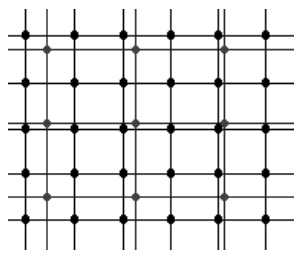
рис. 4.43 черным цветом показана исходная
дискретная целочисленная решетка.
Величины, расположенные в узлах этой
решетки известны: это яркости
соответствующих составляющих в
исходном изображении. Синим цветом
показана новая сетка, в узлах которой
требуется вычислить значения цветовых
составляющих. Восстановление уровней
яркости в узлах новой сетки и называется
“передискретизацией”. Поскольку
координаты чаще всего не попадают в
узлы дискретной решетки (рис. 2.3), то
возникает задача восстановления
соответствующего значения яркости по
ближайшим узлам. Она решается с помощью
методов двумерной интерполяции. Именно
эти методы и определяют качество
результирующего изображения.
Интерполяционное ядро имеет значительное
влияние на численное поведение
интерполированных функций. Теоретически
оптимальную интерполяцию обеспечивает
известная sinc-функция, в
одномерном случае имеющая вид:
а
рис. 4.43 черным цветом показана исходная
дискретная целочисленная решетка.
Величины, расположенные в узлах этой
решетки известны: это яркости
соответствующих составляющих в
исходном изображении. Синим цветом
показана новая сетка, в узлах которой
требуется вычислить значения цветовых
составляющих. Восстановление уровней
яркости в узлах новой сетки и называется
“передискретизацией”. Поскольку
координаты чаще всего не попадают в
узлы дискретной решетки (рис. 2.3), то
возникает задача восстановления
соответствующего значения яркости по
ближайшим узлам. Она решается с помощью
методов двумерной интерполяции. Именно
эти методы и определяют качество
результирующего изображения.
Интерполяционное ядро имеет значительное
влияние на численное поведение
интерполированных функций. Теоретически
оптимальную интерполяцию обеспечивает
известная sinc-функция, в
одномерном случае имеющая вид:

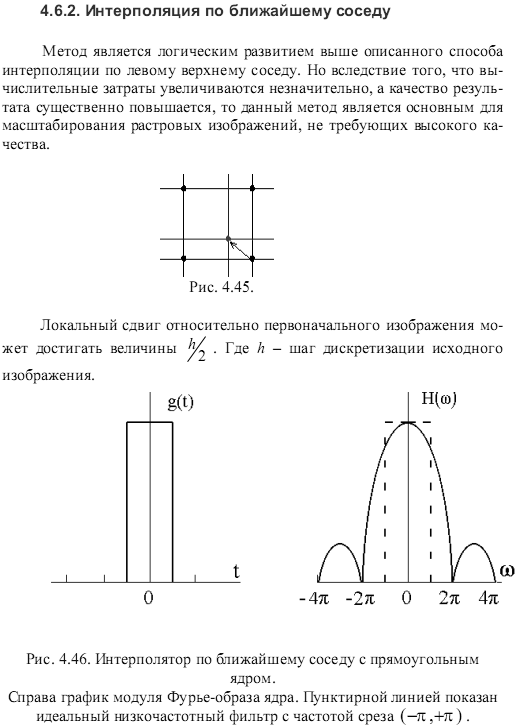

Математическое описание метода состоит в следующем:
• вычисляется диагональ прямоугольника исходной сетки Dgnl;
• вычисляется расстояние от каждого узла до заданной точки и разность с диагональю:
R0= Dgnl – D0;
R1= Dgnl – D1;
R2= Dgnl – D2;
R3= Dgnl – D3;
• вычисляется сумма этих расстояний
SumR= R0+R1+R2,+R3 ;
• вычисляется значение цветовой составляющей в точке:
V= (A R0+B R1+C R2+D R3)/SumR .
Линейная интерполяция
Для реализации этого метода необходимо по исходному дискретному набору данных восстановить непрерывное изображение. После чего осуществить дискретизацию полученного непрерывного изображения. Для восстановления непрерывного изображения используются плоскостная интерполяция.
Для того чтобы получить уравнение плоскости необходимо знать координаты 3-х точек. Уравнение задается в матричной форме:
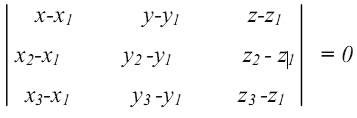
Вычислив определитель и выразив координату z=f(x,y) мы получим формулу, приемлемую для вычисления цветовых составляющих в точках, лежащих внутри ячейки исходной сетки. Но как показывает анализ решаемой задачи, полученную формулу можно значительно упростить, если ввести ограничения, накладываемые практической реализацией. Для примера рассмотрим произвольную ячейку исходной сетки.
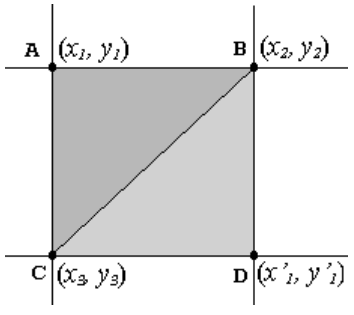
Если точка, яркость которой необходимо вычислить, расположена внутри треугольника АВС, то уравнение плоскости рассчитывается с использованием координат этих точек. Если же точка принадлежит треугольнику BDС, то плоскость рассчитывается по этим 3 точкам, с учетом того, что за (x1, y1) принимаются координаты точки D(x’1, y’1).
На практике отсчет координат ведется от левого верхнего угла ячейки, с учетом того, что шаг дискретизации входного изображения, равен единице, координаты узлов принимают следующие значения:
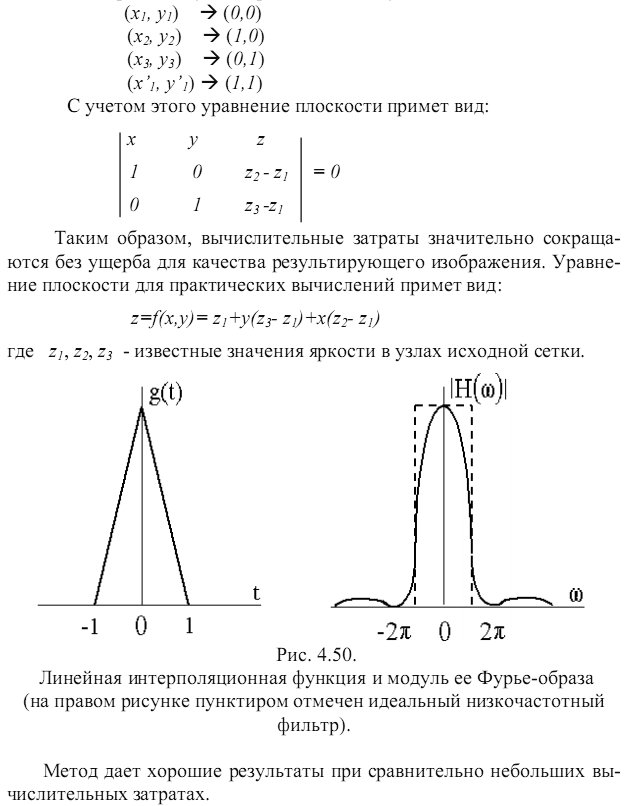

Конец 28 вопроса.
