55.Функция ослабления света на микрогранях в модели освещения с учетом микрогеометрии поверхностей объектов.

. Ослабление света G возникает при падении света на поверхность, что при определенных углах падения светового потока на поверхность обладающую микрорельефом, то микрогррань может оказаться в тени другой микрограни либо сами могут перекрывать потоки света. На практике возможно три случая:

• нормальное падение света;

• затенение микрограней;

• перекрытие отраженного света.

На рис.6.13 использованы следующие обозначения: l – средняя длина микрограни, которая состоит из двух участков: а – затененного (не отражающего) и b – освещенного (отражающего). Степень затенения определяется отношением: a/l . Для первого варианта коэффициент ослабления света G будет иметь величину GТН = 1.

Во втором варианте степень затенения будет выражаться величиной

и будет лежать в пределах [0;1]. В третьем варианте данная величина также будет меньше 1. Это объясняется тем, что часть светового потока перекрывается соседней гранью и не поступает к наблюдателю:

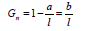
Используя соотношения геометрии можно вывести соотношения для коэффициентов:

Для единичной микрограни одновременно может иметь место только один из трех случаев. Поэтому оценка коэффициента рассчитывается следующим образом:

Коэффициент зеркального отражения rз зависит от λ и угла падения света на поверхность α. Следовательно свет зеркальных бликов должен меняться в зависимости от α. Если свет падает перпендикулярно(α = 0), то блики окрашиваются в цвет поверхности. Если свет близок к скользящему (α 􀂨 900), то блики приобретают цвет источника. В большинстве случаев используют упрощенную формулу зависимости между цветом блика, длиной волны и углом падения. В модели Кука-Торрэнса используется следующая формула:

Здесь Си – цвет источника света, Сп – цвет поверхности. Этот показатель рассчитывается отдельно для каждой из компонент цвета – R, G, B.

56.Моделирование прозрачности и теней.

Для получения наиболее реалистичных изображений кроме отраженного света необходимо учитывать его преломление различными прозрачными и полупрозрачными объектами и средами. При этом необходимо учитывать соотношение, определяемое законом Снелиуса:

где η1, η2 – показатели преломления двух сред; ϕ – угол падения; ψ – угол

преломления.Падающий и преломленный лучи должны находится в одной плоскости. Ни

одно из прозрачных веществ или сред не пропускает свет полностью, т.е. при

наличие эффекта преломления обязательно будет происходить частичное отражение светового потока.

Преломление света бывает двух видов:

• направленное (зеркальное);

• диффузное.

Направленное преломление характерно для прозрачных веществ и сред. При этом искажения возникают только за счет криволинейной поверхности объекта или возмущений поверхности среды.

Диффузное преломление учитывает рассеивание световой энергии при прохождении света через вещество. При этом возникает эффект полупрозрачности или матового изображения. Формулы моделирования прозрачности объектов и сред являются составной частью алгоритмов отсечения невидимых поверхностей. В простейшем случае,

при обработке 3D прозрачная поверхность рассчитывается как линейная комбинация с находящейся за ней поверхностью:

I=I1t1+I2(1-t)

где I1, I2 – интенсивности отраженного света соответственно прозрач-

ной поверхности и поверхности, находящейся за ней; t – определяет

степень прозрачности и находится в интервале [0;1].

При t=0 моделируется максимальная прозрачность рассматриваемого объекта. А при t=1 объект, находящийся на первом плане полностью не прозрачен. Изменяя величину параметра t в ходе 3D-моделирования можно, для достижения максимальной демонстративности, добиваться удаления поверхности.Кроме того, это соотношение можно применять рекурсивно, моделируя таким образом ряд прозрачных объектов, находящихся один за другим.

Для моделирования объектов и поверхностей, имеющих сложные криволинейные формы, моделирование прозрачности при помощи линейной комбинации будет создавать не реалистичный эффект. Поэтому для таких объектов используется не линейная аппроксимация по следующей формуле:

где tmin, tmax – предельные значения прозрачности объектов; nz – проекция нормали к поверхности на ось OZ; P – коэффициент, определяющий кривизну поверхности.

В результате применения этого соотношения прозрачность пикселя t будет меняться в зависимости от расположения этого пикселя на поверхности.

В практике 3D-моделирования достаточно часто используются алгоритмы, работающие на основе Z-буфера (буфер глубины). Но в этой группе алгоритмов напрямую не возможно использовать много-световые эффекты, в том числе эффект моделирования прозрачности.

Это объясняется тем, что данные алгоритмы сохраняют z координаты только для ближайших к наблюдателю объектов.

Чтобы устранить этот недостаток, в алгоритмах с Z-буфером формируется специальный буфер прозрачности. Кроме того, в более сложные алгоритмы могут дополняться дополнительными буферами интенсивности и коэффициентов преломления.

. Моделирование теней

Тени на объектах сцены наблюдаются в том случае, если положение источника света и наблюдателя не совпадают. Тень состоит из двух частей:

• полной тени;

• полутени.

Полная тень – это темная, резко ограниченная область, которая создается точечным источником света. Полутень – это тень, которая создается распределенным источником света, имеющим конечный размер. Она охватывает полную тень по периметру, образуя размытые края. Объем вычислений при расчете теней, кроме всего прочего, зависит от расположения источников света. Возможны три варианта расположения:

1) источник света расположен в бесконечности, при этом направление лучей света, по которым просчитываются тени, соответствует

ортогональному проецированию, т.е. простейшему виду проецирования, а это определяет минимальные затраты на вычисление теней в данном случае;

2) источник света находится на конечном расстоянии вне поля зрения наблюдателя (камеры); в этом случае отслеживание лучей совпадает с перспективным проецированием, что увеличивает вычислительные затраты;

3) источник света находится на конечном расстоянии и попадает в поле зрения наблюдателя; этот случай аналогичен предыдущему, но требует дополнительных затрат на деление сцены по секторам и индивидуальный просчет.

При построении теней выполняется операция, реализующаяся за два шага:

1) построение тени в 3D-виде или относительно источника;

2) построение тени в двумерном виде или относительно наблюдателя.

При этом можно выделить собственные тени объектов и тени

проекционные, образуемые на поверхности объекта другими объектами сцены.

Алгоритм построения собственных теней аналогичен удалению

невидимых поверхностей. А алгоритм построения проекционных теней сводится к построению проекции всех не лицевых граней объектов на сцену. Центр проекции – источник света. При перемещении наблюдателя не надо выполнять пересчет теней, т.к. их положение в 3D сцене зависит от положения источника света.

Конец 56 вопроса.