53.Учет коэффициента Френеля в модели освещения с учетом микрогеометрии поверхностей объектов.

. Коэффициент Френеля F, использующийся в выражении (6.19), определяет закон отражения луча света на границе двух сред для неполяризованного потока излучения.

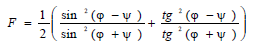
(6.20)

Здесь Ψ – угол преломления.

Согласно закону Снелиуса для угла падения и угла отражения соблюдаются следующие

соотношение:

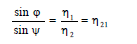
Значение показателя преломления η не является постоянной величиной. Оно зависит от длины волны падающего света и от характеристик вещества поверхности. Поэтому коэффициент

Френеля можно представить как функцию:

Если падающий свет поляризован, то коэффициент Френеля вычисляется по более простым формулам. Если плоскость поляризованного излучения совпадает с плоскостью падения, то коэффициент рассчитывается по формуле:

Если плоскость поляризованных колебаний света перпендикулярна плоскости падения, то:

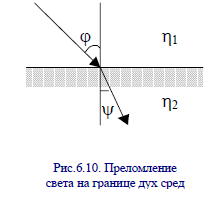
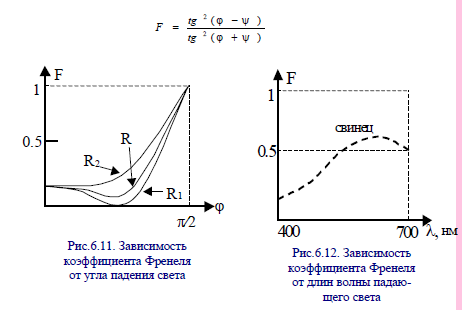
На рис.6.11 приведены зависимости коэффициента Френеля от угла падения света на моделируемую поверхность (R – неполяризованный свет; R1 – поляризованные колебания, находящиеся в плоскости падения световой волны; R2 – плоскость колебаний поляризованного света, перпендикулярна плоскости падения световой волны). На рис.6.12 приведен пример зависимости коэффициента Френеля от длины волны падающего на моделируемую поверхность света. Закон изменения η чаще всего известен для случая нормального падения луча на поверхность (ϕ = 0°). Чтобы определить его зависимость от λ и учесть эту зависимость в формуле (6.20), проведем следующие преобразования. Пусть известна зависимость F0(λ) при нормальном падении луча на микро грань (ϕ = 0°). Для определения произвольной зависимости F(λ), выведем значение η(λ). Обозначим cos ϕ= с , η2 + с2 – 1 = g2.

Тогда формула (6.20) будет иметь следующий вид:

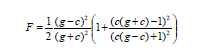
При нормальном падении луча (ϕ=0°) формула (6.21) вырождается в следующую формулу:

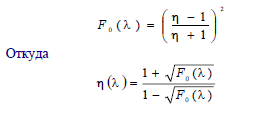
Конец 53 вопроса.

54.Функция распределения микрограней в модели освещения с учетом микрогеометрии поверхностей объектов.

В модели Торрэнса –Сперроу для вычисления функции распределения микрограней D использовалось распределение Гаусса:

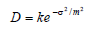
где k – произвольно определяемая константа; δ - угол между двумя нормалями; m – средний квадратичный наклон микро рани относительно уровня макро поверхности.

При определении функции распределения D наибольшую трудность вызывало определение коэффициента k, который невозможно было связать с реальными параметрами геометрических объектов. Поэтому в модели Торрэнса – Кука вместо распределения Гаусса предлагалось использовать распределение Бекмана:

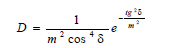
При малых значениях m интенсивность света концентрируется в направлении зеркального отражения, и поверхность выглядит блестящей. При увеличении m интенсивность распределяется более равномерно, при этом поверхность приобретает матовый характер. На практике,при малых значениях m, функции Гаусса и Бекмана практически совпа-

дают. При увеличении m разница между двумя функциями становится заметной.

Если поверхность состоит из микро граней различного размера, то в качестве функции распределения выбирается линейная комбинация следующего вида:

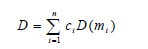
где n – количество типов микрограней, т.е. микрограней имеющих одинаковый наклон; ci – весовые коэффициенты; D(mi) – функция распределения D для i типа микро грани.

Конец 54 вопроса.